由下面的这棵树来分析
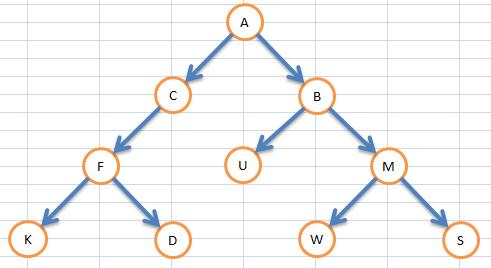
前序遍历:
ACFKDBUMWS
中序遍历:
KFDCAUBWMS
实际前序遍历的组成是
根节点+左边+右边
实际中序遍历的组成是
左边+根节点+右边
step1
前序遍历的第一个为根结点 ,所以A为根节点,
step2
在中序中找到A,分为两组
KFDC 根节点左边
UBWMS 根节点右边
而前序遍历中也可以分开了(只是顺序不一样,个数一样)
CFKD 是左边
BUMWS是右边
step 3
在左边CFKD重新作为一颗整树,重复步骤一和步骤二,根节点为C,
在中序中找到C,在分为左右边,
理论是可以实现重新构建一棵树,如何用编程语言实现?
采用一种递归方法
前序遍历
根+左+右
中序遍历
左+根+右
伪代码
struct node
{
char data;
struct node* left;
struct node* right;
}
struct node* creat(前序遍历字符串f,中序遍历字符串m)
{
struct node n;
n.data=从f中获取根;
fl=前序遍历根的左边;
fr=前序遍历根的右边;
ml=中序遍历根的左边;
mr=中序遍历根的右边;
n.left=creat(fl.ml);
n.right=creat(fr,mr);
return n;
}
还有一个问题,递归的结束问题,什么时候结束。
以一个简单例子说明
前序遍历
ABC
中序遍历
BAC
根A+左B+右C
左B+根A+右C
进入creat函数后
f=“ABC”; m=“BAC”
fl=‘B’ ;fr=’C’
ml=’B’ ; mr=’C’
然后fl和ml进入递归
f=‘B’;m=‘B’
此时,就不再出现左子树和右子树了,很明显这个时候可以全身而退了。
左子树个数=0;
右子树个数=0;
说明左右子树都没有了这是就退
伪代码
struct node
{
char data;
struct node* left;
struct node* right;
}
struct node* creat(前序遍历字符串f,中序遍历字符串m)
{
struct node n;
n.data=从f中获取根;
fl=前序遍历根的左边;
fr=前序遍历根的右边;
ml=中序遍历根的左边;
mr=中序遍历根的右边;
if(左子树长度==0)
{
n.left=NULL;
}
else
n.left=creat(fl.ml);
if(右子树长度==0)
{
n.right=NULL;
}
else
{
n.right=creat(fr,mr);
}
return n;
}c代码实现
#include <iostream>
#include <fstream>
#include <string>
#include <algorithm>
using namespace std;
typedef struct node
{
char data;
struct node* left;
struct node* right;
}NODE;
//qian creat
NODE* creat_node(string &f,string &m)
{
char c;
string fl,fr;
string ml,mr;
int local;
c=f[0];
if(c>'Z' || c<'A')
{
cout<<"error data"<<endl;
exit(-1);
}
local=m.find(c);
if(local == -1)
{
cout<<"not find local"<<endl;
exit(-1);
}
ml=m.substr(0,local);
mr=m.substr(local+1,m.size()-1-local);
fl=f.substr(1,ml.size());
fr=f.substr(fl.size()+1,mr.size());
NODE* node=new NODE;
node->data = c;
if(local == 0)
node->left = NULL;
else
node->left = creat_node(fl,ml);
if((m.size()-1-local)==0)
node->right = NULL;
else
node->right = creat_node(fr,mr);
return node;
}
void front_search(NODE* root)
{
if(root == NULL)
return;
NODE node=*root;
cout<<node.data;
front_search(node.left);
front_search(node.right);
}
void back_search(NODE* root)
{
if(root == NULL)
{
return ;
}
NODE node = *root;
back_search(node.left);
back_search(node.right);
cout<<node.data;
}
int main()
{
string front;
string mid;
freopen("t.txt","r",stdin);
NODE* head;
if((head=new NODE)==NULL)
{
cout<<"new head error"<<endl;
exit(-1);
}
getline(cin,front);
getline(cin,mid);
head=creat_node(front,mid);
front_search(head);
back_search(head);
return 0;
}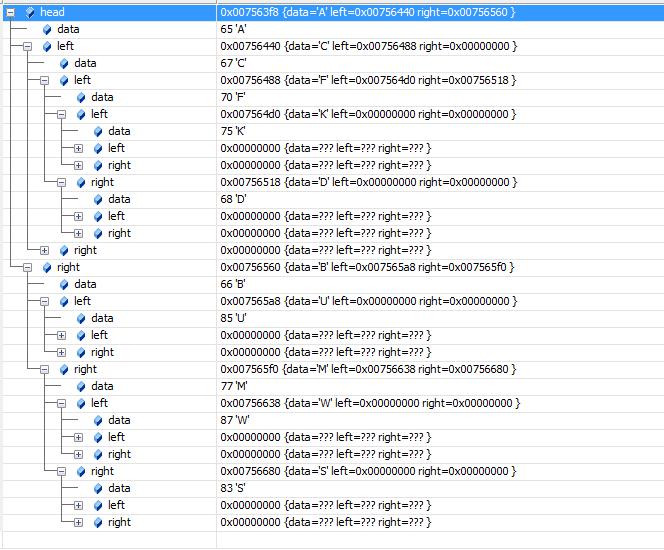
这棵树重构成功
这个问题源于这样的小编程题目
题目
描述:
二叉树的前序、中序、后序遍历的定义:
前序遍历:对任一子树,先访问跟,然后遍历其左子树,最后遍历其右子树;
中序遍历:对任一子树,先遍历其左子树,然后访问根,最后遍历其右子树;
后序遍历:对任一子树,先遍历其左子树,然后遍历其右子树,最后访问根。
给定一棵二叉树的前序遍历和中序遍历,求其后序遍历(提示:给定前序遍历与中序遍历能够唯一确定后序遍历)。
题目类别: 树
难度: 中级
运行时间限制: 无限制
内存限制: 无限制
阶段: 入职前练习
输入:
两个字符串,其长度n均小于等于26。
第一行为前序遍历,第二行为中序遍历。
二叉树中的结点名称以大写字母表示:A,B,C….最多26个结点。
输出:
输入样例可能有多组,对于每组测试样例,
输出一行,为后序遍历的字符串。
样例输入:
ABC
BAC
FDXEAG
XDEFAG
样例输出:
BCA
XEDGAF
























 7628
7628

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








