数据结构之树

最新推荐文章于 2024-08-29 22:43:47 发布
原创 最新推荐文章于 2024-08-29 22:43:47 发布 · 690 阅读 · 2 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

树相关的概念

对于大量的输入数据，链表的线性访问时间太长了，不宜使用，那么就需要一种多分支的访问情况，这个就是树。通过在节点里面增加链接个数，减少访问次数。树是各种算法实现的基础，很多算法都是以树作为基础的。给树再添加一些规则进行操作，从而实现高效的算法。

树状图是一种数据结构，它是由n（n>=1）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：每个节点有零个或多个子节点；没有父节点的节点称为根节点；每一个非根节点有且只有一个父节点；除了根节点外，每个子节点可以分为多个不相交的子树。

  • 父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点。
  • 子节点：一个节点含有的子树的根节点称为该节点为子节点
  • 叶节点：没有儿子的节点。
  • 兄弟节点：具有相同父亲的节点。
  • 节点的度：一个节点含有的子树的个数称为该节点的度，叶节点度为0。
  • 树的度：一棵树中，最大的节点的度称为树的度。
  • 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推。
  • 树的高度：树中节点的最大层次。

树的实现

每一个节点除了数据外还有一些链接其他的指针。

树的遍历

树的遍历全部通过递归实现。

  • 前根序遍历：先遍历根结点，然后遍历左子树，最后遍历右子树。
  • 中根序遍历：先遍历左子树，然后遍历根结点，最后遍历右子树。
  • 后根序遍历：先遍历左子树，然后遍历右子树，最后遍历根节点。
  • 宽度优先遍历：先访问树的第 一层结点 ， 再访问树的第二层结点……一直到访问到最下面一层结点。在同一层结点中， 以从左到右的顺序依次访问。
/*
* 前序遍历伪代码
*/
static void preorder(RBTree tree)
{
     if(tree != NULL)
     {
         printf("%d ", tree->key);
         preorder(tree->left);
         preorder(tree->right);
     }
}

 /*
 * 中序遍历伪代码
 */
static void inorder(RBTree tree)
{
     if(tree != NULL)
     {
         inorder(tree->left);
         printf("%d ", tree->key);
         inorder(tree->right);
     }
}

/*
* 后序遍历伪代码
*/
 static void postorder(RBTree tree)
 {
     if(tree != NULL)
     {
         postorder(tree->left);
         postorder(tree->right);
         printf("%d ", tree->key);
     }
 }

这里写图片描述

二叉树

每个节点都不能有多余两个儿子的树。在查找里面有用到。依次结点排列的顺序分为满二叉树和完全二叉树

  • 满二叉树：在一棵二叉树中，如果所有分支结点都存在左子树和右子树。并且所有叶子结点都在同一层上，这样的一棵二叉树称为满二叉树。
  • 完全二叉树：就是一颗二叉树结点按照优先从上到下，从左到右依次排列，满二叉树肯定是完全二叉树 ， 而完全二叉树不一定是满二叉树。完全二叉树在堆排序中有应用。

二叉树的基本性质如下：

  • 性质1：一棵非空二叉树的第i层上最多有2^(i-1)个结点。
  • 性质 2: 一棵深度为k的二叉树中，最多具有 2^(k-1)个结点，最少有 k 个结点。
  • 性质 3 : 对于一棵非空的二叉树，度为0的结点(即叶子结点)总是比度为2的结点多1个，即如果叶子结点数为n0，度数为2的结点数为02，则有 n0 = n2 + 1。
  • 性质 4: 具有n个结点的完全二叉树的深度为 log2(n) + 1。
    这里写图片描述
    这里写图片描述

二叉树的后序遍历序列为 DGJHEBIFCA，中序遍历DBGEHJACIF则其先序遍历序列为多少?
二叉树的先序序列为ABDECF，中序序列为DBEAFC，求后序遍历序列为多少？

一颗二叉树，其前序遍历为abcdefg，可能的中序遍历有：ABD
A. abcdefg
B. gfedcba
C. gabcdef
D. cdefbag

特殊二叉树之二叉搜索树

对于节点X，其左子树的项值小于X里面项值，右子树的项值大于X里面项值。所有元素都可以通过某种方式排列，因此在查找里面广泛用到。在二叉搜索树中 ， 左子结点总是小于或等于根结点，而右子结点总是大于或等于根结点。从根节点一直往左走，直到无左路可走，及得到最小元素；从跟节点一直往右走，直至无路可走，及得到最大元素。

实现见链接。

特殊二叉树之堆

堆分为最大堆和最小堆，堆是一种完全二叉树。在最大堆中根结点的值最大，在最小堆中根结点的值最小。有很多需要快速找到最大值或者最小值的问题都可以用堆来解决。其中lib时间管理就是通过堆实现的。

2-3树

一种树的概念，但是实现通过红黑树。

红黑树

红黑树是把树中的结点定义为红、黑两种颜色，并通过规则确保从根结点到叶结点的最长路径的长度不超过最短路径的两倍，红黑树是实现2-3树的一种具体方式，在查找里面有广泛的应用。
实现见链接。

二叉树重要题目合集

1、二叉树四种遍历递归及非递归实现

https://blog.csdn.net/xiaominkong123/article/details/51567437
https://www.cnblogs.com/gl-developer/p/7259251.html
https://www.cnblogs.com/fly-me/p/wei-ti-jiaoer-cha-shu-de-si-zhong-bian-li-fang-fa.html

1、前序：
非递归实现：
根据前序遍历访问的顺序，优先访问根结点，然后再分别访问左孩子和右孩子。即对于任一结点，其可看做是根结点，因此可以直接访问，访问完之后，若其左孩子不为空，按相同规则访问它的左子树；当访问其左子树时，再访问它的右子树。因此其处理过程如下，对于任一结点P：
1)访问结点P，并将结点P入栈;
2)判断结点P的左孩子是否为空，若为空，则取栈顶结点并进行出栈操作，并将栈顶结点的右孩子置为当前的结点P，循环至1);若不为空，则将P的左孩子置为当前的结点P;
3)直到P为NULL并且栈为空，则遍历结束。

2、中序：
根据中序遍历的顺序，对于任一结点，优先访问其左孩子，而左孩子结点又可以看做一根结点，然后继续访问其左孩子结点，直到遇到左孩子结点为空的结点才进行访问，然后按相同的规则访问其右子树。因此其处理过程如下，对于任一结点P，
　1)若其左孩子不为空，则将P入栈并将P的左孩子置为当前的P，然后对当前结点P再进行相同的处理；
　 2)若其左孩子为空，则取栈顶元素并进行出栈操作，访问该栈顶结点，然后将当前的P置为栈顶结点的右孩子；
　3)直到P为NULL并且栈为空则遍历结束。
　
3、后序：
后序遍历的非递归实现是三种遍历方式中最难的一种。因为在后序遍历中，要保证左孩子和右孩子都已被访问并且左孩子在右孩子前访问才能访问根结点，这就为流程的控制带来了难题。下面介绍两种思路。
第一种思路：对于任一结点P，将其入栈，然后沿其左子树一直往下搜索，直到搜索到没有左孩子的结点，此时该结点出现在栈顶，但是此时不能将其出栈并访问， 因为其右孩子还未被访问。所以接下来按照相同的规则对其右子树进行相同的处理，当访问完其右孩子时，该结点又出现在栈顶，此时可以将其出栈并访问。这样就保证了正确的访问顺序。可以看出，在这个过程中，每个结点都两次出现在栈顶，只有在第二次出现在栈顶时，才能访问它。因此需要多设置一个变量标识该结点是否是第一次出现在栈顶。

struct TreeNode{
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
};

//二叉树前序遍历 根 左 右
void PreoderRecursion(TreeNode *pRoot)
{
    if(pRoot == NULL)//返回
        return ;
    cout << pRoot->val;
    Preoder(pRoot->left);
    Preoder(pRoot->right);
}

void Preoder(TreeNode *pRoot)
{
    stack<TreeNode *>s;
    while(pRoot != NULL || !s.empty()){
        while(pRoot != NULL){//将左子树全部压栈
            s.push(pRoot);
            cout << pRoot->val;
            pRoot = pRoot->left;
        }
        if(!s.empty()){
            pRoot = s.top();
            s.pop();
            pRoot = pRoot->right;
        }
    }
}

//二叉树中序遍历  左 根 右
void inOderRecursion(TreeNode *pRoot)
{
    if(pRoot == NULL)//返回
        return ;
    Preoder(pRoot->left);
    cout << pRoot->val;
    Preoder(pRoot->right);
}

void Preoder(TreeNode *pRoot)
{
    stack<TreeNode *>s;
    while(pRoot != NULL || !s.empty()){
        while(pRoot != NULL){//将左子树全部压栈
            s.push(pRoot);
            pRoot = pRoot->left;
        }
        if(!s.empty()){
            pRoot = s.top();
            cout << pRoot->val;
            s.pop();
            pRoot = pRoot->right;
        }
    }
}

//二叉树后序遍历 左 右 根   通过一个栈实现，1、左右都遍历完了再遍历根。2、左右已经遍历完了 否则先压右子树再左子树
void PostOderRecursion(TreeNode *pRoot)
{
    if(pRoot == NULL)//返回
        return ;
    Preoder(pRoot->left);
    Preoder(pRoot->right);
    cout << pRoot->val;
}

void PostOder(TreeNode *pRoot)
{
    stack<TreeNode *>s;
    TreeNode *hasVisit = NULL;
    if(pRoot != NULL){
        s.push(pRoot);
        while (!s.empty()) {
            pRoot = s.top();
            if( (pRoot->left == NULL && pRoot->right == NULL) ||
                    ((pRoot->left != NULL || pRoot->right != NULL) && hasVisit != NULL)){//没有左右孩子，或者有且访问过了，则可以访问此节点
                cout <<pRoot->val;
                hasVisit = pRoot;//标记此节点已经访问了
                s.pop();
            }else{//否则压入 右子树和左子树
                if(pRoot->right != NULL)
                    s.push(pRoot->right);
                if(pRoot->left != NULL)
                    s.push(pRoot->left);
            }
        }
    }
}

//二叉树广度（层序）通过一个队列实现
//入队，弹出，访问，左右子树入队，循环上述过程
void BFSOder(TreeNode *pRoot)
{
    queue<TreeNode *> q;
    if(pRoot == NULL)//防御性编程
        return ;
    q.push(pRoot);
    while (!q.empty()) {
        pRoot = q.front();
        q.pop();
        cout << pRoot->val;

        if(pRoot->left != NULL)//入队
            q.push(pRoot->left);

        if(pRoot->right != NULL)//入队
            q.push(pRoot->right);
    }
}

已知先序遍历和中序遍历求后序遍历

重建二叉树

这里写图片描述

题目：:输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列 {1， 2， 4， 7， 3， 5， 6， 8}和中序遍历序列 {4，7，2，1，5，3，8，6｝，则重建如图所示的二叉树并输出它的头结点。

8、求二叉树中节点的最大距离

9、树的子结构

输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构），注意二叉树并非二叉查找树。
利用vector实现起来就很容易了。第一种方法容易理解，第二种方法难以理解。

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/
class Solution {
public:
    /*
    两个前序遍历，将节点压入vector，然后判断连续数字序列即可，这个方法比较慢，效果很不好的哦。

    vector<int> T1 , T2;
    bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2)
    {
        //注意下述防御性编程的理解。
        if(pRoot1 != NULL && pRoot2 != NULL){//任意一个为空，则为返回假
            PreOrder(pRoot1 , T1);//中序遍历起来
            PreOrder(pRoot2 , T2);//中序遍历起来
            if(T1.size() > T2.size()){
                for(int i = 0 ; i <= (T1.size()- T2.size()) ; i++){
                        for(int j = 0 ; j < T2.size() ; j++){//连续后面T2个是否相等？
                            if(T1[i+j] != T2[j])
                                break;
                            if(j == T2.size() -1)//成功找到
                                return true;
                        }
                    }
                return false;//没有找到
            }else
                return false;
        }else
            return false;

    }
    void PreOrder(TreeNode* pRoot , vector<int> &a){
        if(pRoot != NULL){
            a.push_back(pRoot->val);//前序遍历
            PreOrder(pRoot->left , a);
            PreOrder(pRoot->right , a);
        }
    }*/
    /*
    不需要全部遍历完，则分两步走：
    1、先找到A中和B根节点一样节点。
    2、从当前节点比较下去，直到树B为空为真
    */
    bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2)
    {
        //注意下述防御性编程的理解。
        bool result = false;
        if(pRoot1 != NULL && pRoot2 != NULL){//主循环是前序遍历，次循环也是前序遍历。
            if(pRoot1 ->val == pRoot2 ->val)//树A节点等于树B的根节点，那么可以继续玩下去了，否则继续遍历树A
                result = If_tree1_have_tree2(pRoot1 , pRoot2);//继续找下去
            if(result == false)//写出让别人容易看懂的代码，取消难以看懂的地方，尽量简单的写，类似Redis的作者，代码简答又有逻辑。
                result = HasSubtree(pRoot1->left , pRoot2);//递归左子树
            if(result == false)
                result = HasSubtree(pRoot1->right , pRoot2);//递归右子树
        }
        return result;
    }
    bool If_tree1_have_tree2(TreeNode* pRoot1, TreeNode* pRoot2){//递归找到下面的是不是子树

        if(pRoot2 == NULL)//可以递归找到树B为空，那么肯定是其子树
            return true;
        if(pRoot1 == NULL)//找到树A为空，则必定不是子树
            return false;
        if(pRoot1 ->val != pRoot2 ->val)//找的中途结束
            return false;

        //再对比树A和B左节点  然后比较树A和树B的右节点，一直比下去。
        return If_tree1_have_tree2(pRoot1->left , pRoot2->left) && 
               If_tree1_have_tree2(pRoot1->right , pRoot2->right);//利用短路特性。
    }
};

10、二叉树的镜像

这里写图片描述
思路：先前序遍历这棵树的每个节点，如果遍历到的节点有子节点，就交换它的两个子节点。当交换完成了所有非叶子节点之后，就得到树的镜像。
递归：前序操作，然后交换。
循环：通过栈，操作，然后循环。
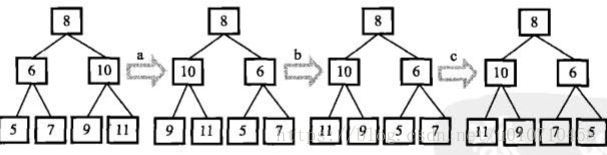
这里写图片描述
重点在于利用二叉树的前序遍历。

//二叉树镜像的递归及非递归实现
class Solution {
public:
    void Mirror(TreeNode *pRoot) {
        if(pRoot == NULL)//空树返回
            return;
        stack<TreeNode*> stackNode;//栈用来保存节点
        stackNode.push(pRoot);
        while( stackNode.size() ){
            TreeNode* tree = stackNode.top();//读取节点
            stackNode.pop();//弹出
            if(tree->left != NULL || tree->right != NULL){//交换左右节点
                TreeNode *ptemp = tree->left;
                tree->left = tree->right;
                tree->right = ptemp;
            }
            //然后重复操作
            if(tree->left)//左子树非空
                stackNode.push(tree->left);//左节点压栈
            if(tree->right)
                stackNode.push(tree->right);//右节点压栈
        }
    }
    /*前序遍历一次，则可以解决问题
        void Mirror(TreeNode *pRoot) {
            if(pRoot == NULL)
                return ;
            if(pRoot->left != NULL || pRoot->right != NULL){
                TreeNode *ptemp = pRoot->left;
                pRoot->left = pRoot->right;
                pRoot->right = ptemp;
            }
            if(pRoot->left != NULL)
                Mirror(pRoot->left);
            if(pRoot->right != NULL)
            Mirror(pRoot->right);                
        }    
    */
};

11、判断二叉树是否对称

请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。

/*

            8
           /  \
          2   2
         / \  / \
        4  3 3   4
上述是一颗对称二叉树。总结：
1、根节点以及其左右子树数据相同
2、左子树的左子树和右子树的右子树数值相同
3、左子树的右子树和右子树的左子树数值相同

*/
class Solution {
public:
    bool isSymmetrical(TreeNode* pRoot)
    {
        if(pRoot == NULL){
            return true;
        }
        return comRoot(pRoot->left, pRoot->right);//从根的左右子树开始
    }
private: 
    //如果对称，则返回真。
    bool comRoot(TreeNode* left, TreeNode* right) {
        if(left == NULL && right == NULL)//左右都为空，返回真。直接返回，这层对称
            return true;
        if( (left == NULL && right != NULL) || (left != NULL && right == NULL) )//一个为空，一个不为空，返回假，直接返回，非对称
            return false;
        //全部不为空，则比较数值        
        if(left->val != right->val)//不等，直接返回，非对称 
            return false;
        return comRoot(left->right, right->left) && comRoot(left->left, right->right);//继续比较第2和3步，递归实现
    }
};

12、二叉树的深度

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/
class Solution {
public:
    //最终返回某个节点的深度
    int TreeDepth(TreeNode* pRoot)
    {
        /*
        递归思路：
              一棵树只有一个节点，深度是1。树的深度等于其左、右子树深度的较大值+1。
        if(pRoot == NULL)//防御性编程实现
            return 0;
        int nLeft = TreeDepth(pRoot-> left);//左子树深度
        int nRight = TreeDepth(pRoot-> right);//右子树深度
        return (nLeft >　nRight) ? (nLeft + 1 ) : (nRight + 1);//比较，较大则加1。采用递归实现。
        */
    }
};

13、判定平衡二叉树

二叉树、平衡二叉树、红黑树的区别

class Solution {
public:
    bool IsBalanced_Solution(TreeNode* pRoot) {
        /*
            遍历每个节点的时候，调用TreeDepth得到左右子树的高度。如果每个节点的深度不超过1，则是一颗平衡二叉树。
            因为TreeDepth函数，导致许多节点会被重复遍历
         if(pRoot == NULL)//节点没有左右子树，肯定平衡。
             return true;
        int left = TreeDepth(pRoot-> left);//返回左子树深度
        int right = TreeDepth(pRoot-> right);//返回右子树深度
        int diff = left - right;
        if(diff > 1 || diff < -1)//不能超过1
            return false;
        return IsBalanced_Solution(pRoot-> left) && IsBalanced_Solution(pRoot-> right);//继续
        */

        /*
        后序遍历的方式遍历整颗二叉树，在遍历某个节点的左右子节点后，根据左右子节点的深度判断是不是平衡。
        */
        int depth = 0;
        return IsBalanced(pRoot , &depth);
    }
    bool IsBalanced(TreeNode* pRoot , int *pDepth)
    {
        if(pRoot == NULL){
            *pDepth = 0;
            return true;
        }
        int left = 0 , right = 0;
        if( IsBalanced(pRoot-> left , &left) && IsBalanced(pRoot-> right , &right) ){//判断左右子树IsBalanced，并记录深度
            int diff = left - right;
            if(diff <= 1 && diff >= -1){
                *pDepth = 1 + (left > right ? left : right);
                return true;
            }
        }
        return false;
    }
    //返回某个节点的深度
    int TreeDepth(TreeNode* pRoot)
    {
        /*
        递归思路：
              一棵树只有一个节点，深度是1。树的深度等于其左、右子树深度的较大值+1。
        */
        if(pRoot == NULL)//防御性编程实现
            return 0;
        int nLeft = TreeDepth(pRoot-> left);//左子树深度
        int nRight = TreeDepth(pRoot-> right);//右子树深度
        return (nLeft >　nRight) ? (nLeft + 1 ) : (nRight + 1);//比较，较大则加1。采用递归实现。

    }
};

二叉搜索树的第k个节点

给定一颗二叉搜索树，请找出其中的第k大的结点。例如， 5 / \ 3 7 /\ /\ 2 4 6 8 中，按结点数值大小顺序第三个结点的值为4。

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
            5
           /  \
          3    7
         / \  / \ 
        2  4 6   8
 第三个节点是4，注意没有第0个节点和负数节点。一定得注意边界条件的判定。  
*/
class Solution {
public:
    /*
    vector<TreeNode*> a;
    int index = 0;
    TreeNode* KthNode(TreeNode* pRoot, int k)
    {
        if(pRoot != NULL){
            Order(pRoot);//中序遍历压入数组
            //if(k < 0 || k == 0 || a.size() < k)
            if(k > 0 && k <= a.size() )    
                return a[k-1];
            else
                return NULL;
        }
        return NULL;
    }
    void Order(TreeNode* pRoot){
        if(pRoot != NULL){
            Order(pRoot->left);
            if(++index == k)
            a.push_back(pRoot);
            Order(pRoot->right);
        }
    }*/
    /*
    采用中序遍历的非递归形式，时间复杂度是O(k)
    */
    TreeNode* KthNode(TreeNode* pRoot, int k)
    {
        int count = 0;
        stack<TreeNode*> Snode;//栈
        if(k <= 0)
            return NULL;
        while(pRoot != 0 || Snode.size() != 0){
            while(pRoot != NULL){//左子树全部入栈
                Snode.push(pRoot);
                pRoot = pRoot->left;
            }
            if(Snode.size() != 0){
                pRoot = Snode.top();
                if(++count == k)//类似于中序遍历访问即可。
                    return pRoot;
                Snode.pop();//出栈
                pRoot = pRoot->right;
            }
        }
        return NULL;//全部没有，则返回空，因为k比index还要大
    }
};

树中两个节点的最低公共祖先节点

数据结构之树和森林
qq_33501207的博客
01-24 1475
树结构是一种非常重要的非线性结构，该结构中的一个数据元素可以有两个或两个以上的直接后继元素，树可以用来描述客观世界中广泛存在的层次结构关系。森林则有多棵树构成。
数据结构之树（Python代码实现）
Zcoder`Blog
06-04 4055
关于树的概念性我就不作大篇幅的讲解，我在软件设计师笔记之数据结构中对树有较深的概念性笔记，欢迎各位去研究，现在主要是Python代码的实现。 接下来通过Python代码实现树这种数据结构，分别从普通树与二叉树来实现。 一、普通树 实际上树可以通过多维列表来表示，如下代码与图所示 ['根节点',['数据1',['数据3',['数据2']],['数据...
数据结构-树
04-08
树形结构是一层次的嵌套结构。 一个树形结构的外层和内层有相似的结构， 所以这种结构多可以递归的表示。
数据结构树的程序设计
12-08
一个小程序适合初学者,应该还可以 主函数main() 创建二叉树函数CreateBTNode（ ） 先序遍历二叉树函数Preorder（ ） 中序遍历二叉树函数Inorder（　） 　 后序遍历二叉树函数Postorder( ) 层次遍历二叉树函数Levelorder（ ） 查找结点函数Findnode（ ） 查找某结点的左孩子结点Lchildnode（） 查找某结点的右孩子结点Rchildnode（） 求二叉树高度的函数BTNodedepth（ ） 求二叉树中所有结点的函数Nodes（ ） 求二叉树中所有叶子结点的函数 Leafnodes（ ） 输出所创建的二叉树函数DispBTNode（ ） 将二叉树左右孩子交换的函数Revolute(
数据结构初阶：二叉树
yourfriendyo的博客
11-17 1665
树是n(n≥0)n\;(n≥0)n(n≥0)个元素的有限集。树是递归定义的，任意一个树都是由一个根结点和多个子树构成，而其中每个子树也是由一个根结点和多个子树构成。根结点：每个树有且仅有的一个根结点，即树中最上面的一个结点，根结点无前驱结点。子树：分成M(M≥0)M\;(M≥0)M(M≥0)个互不相交的集合，而每个集合都是一个与树结构类似的子树。如右图所示，根结点AAA下面有三个子树，这三个子树又分别以结点BBB，CCC，DDD为根结点。B。
数据结构——树
weixin_33998125的博客
12-07 172
一、树的定义树是n(n>=0)个结点的有限集。n=0时称为空树，在任意一颗非空树：1、有且仅有一个特定的根结点。2、当n>1时其余结点可分为m（m>0)个互不相交的有限集T1、T2、.....Tm，其中每一个集合本身又是一棵树，并且称为根的子树。二、结点的度，拥有的子树称为结点的度如上图结点A的度是2，结点B的度是1，结点C的度是2，结点E的度是3，结点G的度是0度为0的节点...
python数据结构-树总结
KG
08-24 638
python数据结构-树总结树（英语：tree）是一种抽象数据类型（ADT）或是实作这种抽象数据类型的数据结构.
数据结构之生成树及最小生成树
qq_33501207的博客
01-27 1933
对于有n个顶点的连通图，至少有n-1条边，而生成树中恰好有n-1条边，所以连通图的生成树是该图的极小连通子图。对于连通网来说，边是带权值的，生成树的各边也带权值，因此把生成树各边的权值总和称为生成树的权，把权值最小的生成树称为最小生成树。
python数据结构之树形结构
wc199422的博客
04-09 4610
python数据结构 二叉树 树的查询，遍历，存储
数据结构：树
OR的博客
08-15 1608
一、数的定义现实生活中，有很多一对多的情况需要处理，所以我们需要研究这种一对多的数据结构——“树”，考虑到它的各种特性，来解决在编程中碰到的相关问题。树(Tree)是n（n≥0）个结点的有限集。n = 0时称为空树。在任意一棵非空树中：（1）有且仅有一个特定的称为根（Root）的结点；（2）当n ≥ 1时，其余结点可分为m（m>0）个互不相交的有限集T1、T2、……、Tm，其中每一个集合本身又是一棵
前中后序的迭代和递归写法
sdsc1314的博客
09-16 478
前序 递归 class Solution { vector<int> res; public: vector<int> inorderTraversal(TreeNode* root) { if(root ==NULL ) { return res; } res.push_back(root->val); inorderTraversal(root-&gt
二叉树建立
qq_33824968的博客
08-19 197
include <stdio.h> include <stdlib.h> struct TreeNode { int val; struct TreeNode *left; struct TreeNode *right; }; struct TreeNode *CreateNode(int data) { struct TreeNode ...
基本数据结构：树（tree）
主要记录嵌入式学习与开发过程。
09-15 2263
略。
数据结构树（C语言版）
最新发布
weixin_62345907的博客
08-29 1850
树（Tree）是一种非常常见的数据结构，它模拟了一种层级或分支结构。
C语言数据结构(12)--链表描述子节点的树
编程副队长
10-18 654
数组描述子节点的缺点 如果有这么一颗奇葩的树，大多数节点的孩子数为1-2个，但是有一个节点的孩子数是100个。 因为我们使用数组描述子节点，所以描述子节点的数组得定义为struct TreeNode* children[100];。 也就是说，除了有一个充分利用了数组分配的空间，其他的都造成了极大浪费，毫无疑问不合理。 使用链表描述 孩子也是一个一维的集合，特点个数不确定，符合这种特点的数据结构就...
创建和遍历二叉树
zy1994384的博客
12-10 284
创建和遍历二叉树的经验
二叉树的实现
mrbone9的博客
02-19 824
在回忆学生时代学习树这种数据结构时，仅有的回忆就是前中后遍历，其余毫无印记 在工作当中，好像就没有怎么用到，更不用说编码去实现，调试 其实不然，AVL树，红黑树等等都是有实际的应用，所以掌握好基本的知识点还是非常必要的 以最简单常用的基础开始 树的表现： 链表 的形式最为常见，因为树是有分支的，是 非线性的 正如自然界的树，只不过树根在上，分支在下，最末为叶子 我们研究的都是基于 二叉树 二叉树：是 n（n >= 0）个结点的有限集合，该集合或为空集（空二叉树）。或者由一个根节点和
C++中树的数据结构实现方法详解
在了解“数据结构C++树的实现”相关知识点之前，首先要明确几个基本概念。数据结构是计算机存储、组织数据的方式，以便于使用数据结构可以高效地进行数据的插入、删除、查找和修改操作。树是一种重要的非线性数据...
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

有时需要偏执狂

请我喝咖啡

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值