考试的时候遇到个题目根本就没想到和递归有什么关系,现在回想起来阿里考得其实都是算法题目
题目:在如下4*5的矩阵中,请计算从A移动到B一共有______种走法?要求每次只能向上或向右移动一格,并且不能经过P。
方法一:写出每个格子的路径种数,其中,每个格子的路径种数 = 左边格子种数 + 下边格子种数
首先考虑没有阻碍的时候,假设在任意MXN(题上为4X5)的这种格子上,从A出大到B的不同走法为f(M,N),则根据递推可知f(M,N)=f(M-1,N)+f(M,N-1),等号右边两项分别是在当前点向下走一步和向左走一步的情况。递归终止情况为f(1,1)=1;
在有阻碍的时候,如题。
从A出发到X的走法步数为f(4,2),到达X后只有一种走法,即一直向右
从A出发到Y的走法步数为f(2,4),到达Y后有f(3,2)种走法,因此连接的总数为f(2,4)*f(3,2)。
至此唯一没有涵盖的走法为经Z点至B点,此种走法有且仅有1种。
所以总数目为f(4,2)+f(2,4)*f(3,2)+1 = 17;
方法一:利用组合数解决
不考虑经过P:从A到B必须要向上走3步,向右走4步,所以从A到B,一共有C(7,3)种走法
考虑经过P:从A到P必须要向上走2步,向右走2步,所以一共是C(4,2)种
从P到B必须要向上走1步,向右走2步,所以一共是C(3,1)种
则考虑P,从A到B一共有C(7,3)-C(4,2)*C(3,1) = 17种走法









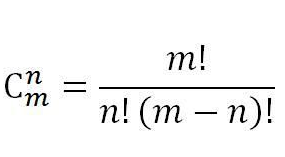














 846
846

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








