【HDU】4658 Integer Partition【生成函数——数拆分】

传送门：【HDU】4658 Integer Partition

题目分析：

用了五边形数定理以及生成函数，然而我看懂了生成函数怎么搞这题却不知道为啥生成函数是五边形数形式= =

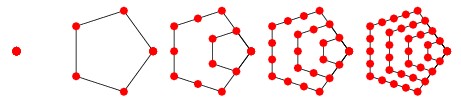
首先观察下面的图片：

很容易我们可以发现用这种方式构造N个五边形（假设一个点也算一个五边形），需要点的个数为：

$$\frac{n*(3n-1)}{2}$$

---

接下来我们来看一下数拆分。
提问：将一个正整数$N$拆成不少于一个数的和，问有多少种方案。

很容易我们可以构造一个多项式：
$P(x)=(1+x^1+x^2+...)(1+x^2+x^4+...)(1+x^3+x^6+...)...$
$=P_x(0)x^0+P_x(1)x^1+P_x(2)x^2+...+P_x(n)x^n$

可以发现N的数拆分的方案数正对应着多项式展开后$x^n$的系数$P_x(n)$

考虑如下等式：

$$(1+x^1+x^2+...)=\frac{1}{1-x}$$
因此我们有：
$$\prod_{i=0}^{\infty}\frac{1}{1-x^i}=\sum_{i=0}^{\infty} P_x(i)x^i$$
其中上式等式左边是欧拉函数 $\phi(x)$的倒数。即：
$$\frac{1}{\phi(x)}=\sum_{i=0}^{\infty} P_x(i)x^i$$

欧拉函数$\phi(x)$的展开式为：

$$\phi(x)=(1-x)(1-x^2)(1-x^3)...=1-x-x^2+x^5+x^7-x^{12}-x^{15}+x^{22}+x^{26}-...$$
其中的x的指数正对应着广义五边形数！

$n$	0	1	-1	2	-2	3	-3	4	-4	…
$P(n)$	0	1	2	5	7	12	15	22	26	…

现在我们要计算$P_x(n)$，由于$\frac{1}{\phi(x)}=P(x)$，亦即$\phi(x)P(x)=1$。

$$(1-x-x^2+x^5+...)(P_x(0)+P_x(1)x+P_x(2)x^2+P_x(3)x^3+...)=1$$
所以： $P_x(n)=P_x(n-1)+P_x(n-2)-P_x(n-5)-P_x(n-7)+...$

由于对于满足$\frac{i(3i-1)}{2}\leq n$的$i$的个数不超过$\sqrt(n)$个，于是计算所有$P_x(n)$的复杂度为$O(n\sqrt(n))$

---

上面我们说明的是不带限制的数拆分，现在我们给定一个限制：拆分出来的每种数的个数不能大于等于k（这也是本题的要求）。

类似的，我们考虑生成函数：

$$(1+x^1+x^2+...+x^{k-1})(1+x^2+x^4+...x^{2(k-1)})...=\prod_{i=0}^{\infty}\frac{1-x^{ki}}{1-x^i}=\frac{\phi(x^k)}{\phi(x)}=\phi(x^k)P(x)$$
展开 $\phi(x^k)$得：
$$(1-x^k)(1-x^{2k})(1-x^{3k})...=1-x^k-x^{2k}+x^{5k}+x^{7k}-x^{12k}-x^{15k}+...$$
然后可得：
$$\phi(x^k)P(x)=(1-x^k-x^{2k}+x^{5k}...)(P_x(0)+P_x(1)x+P_x(2)x^2+P_x(3)x^3+...)$$
令 $F_k(n)$表示n的满足数拆分时每种数的个数小于等于k的数拆分方案数。则有：
$$F_k(n)=P_x(n)-P_x(n-k)-P_x(n-2k)+P_x(n-5k)+...$$

$my~~code:$

#include <stdio.h>
#include <string.h>
#include <math.h>
#include <bitset>
#include <map>
#include <set>
#include <algorithm>
using namespace std ;

typedef long long LL ;

const int MAXN = 100005 ;
const int mod = 1e9 + 7 ;

int p[MAXN] ;
int t1[MAXN] , t2[MAXN] ;
int n , k ;

void add ( int& x , int y ) {
    x += y ;
    while ( x >= mod ) x -= mod ;
    while ( x < 0 ) x += mod ;
}

void preprocess () {
    p[0] = 1 ;
    for ( int i = 1 ; ; ++ i ) {
        t1[i] = i * ( 3 * i - 1 ) / 2 ;
        t2[i] = i * ( 3 * i + 1 ) / 2 ;
        if ( t1[i] >= MAXN ) break ;
    }
    for ( int i = 1 ; i < MAXN ; ++ i ) {
        p[i] = 0 ;
        for ( int j = 1 , flag = 1 ; ; ++ j , flag *= -1 ) {
            if ( t1[j] <= i ) add ( p[i] , flag * p[i - t1[j]] ) ;
            else break ;
            if ( t2[j] <= i ) add ( p[i] , flag * p[i - t2[j]] ) ;
            else break ;
        }
    }
}

void solve () {
    scanf ( "%d%d" , &n , &k ) ;
    int ans = p[n] ;
    for ( int j = 1 , flag = -1 ; ; ++ j , flag *= -1 ) {
        if ( k * t1[j] <= n ) add ( ans , flag * p[n - k * t1[j]] ) ;
        else break ;
        if ( k * t2[j] <= n ) add ( ans , flag * p[n - k * t2[j]] ) ;
        else break ;
    }
    printf ( "%d\n" , ans ) ;
}

int main () {
    int T ;
    preprocess () ;
    scanf ( "%d" , &T ) ;
    for ( int i = 1 ; i <= T ; ++ i ) {
        solve () ;
    }
    return 0 ;
}