Treap

Treap 是一种效率较高、易于编写的平衡二叉查找树，和 splay 一样受到广大竞赛选手的青睐（嗯，我不会 splay）。
在正式介绍 Treap 之前，需要简单回顾一下之前学过的 BST 和堆。

一、BST

定义

二叉查找树 (binary search tree, 简称 BST，也常被译作“二叉搜索树”或“二叉排序树”)，是一棵空树，或满足如下性质的二叉树：

• 若某节点的左子树不为空，则左子树上所有节点的值均小于该节点的值；
• 若某节点的右子树不为空，则右子树上所有节点的值均大于该节点的值；
• 其左、右子树也分别为 BST。
  注意这里讨论的是节点键值不重复的 BST，出现重复键值的情况后面再考虑。
  BST 的性质是非常重要的内容，满足和维护其性质是其一切操作的依据和前提。下图就是一棵 BST。
  

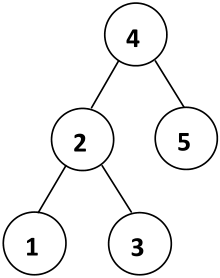
遍历

时间复杂度为 $O(N)$
显然一棵 BST 的中序遍历就是一个单调递增序列。

查找

期望时间复杂度为 $O(log_2N)$
在 BST 中查找某个值的步骤为：从根节点出发，每次考察当前节点的值：
若当前节点为空（查找失败）或等于待查找的值（查找成功）则返回；
若待查找的值小于当前节点的值，则在左子树中查找；否则在右子树中查找。

插入

期望时间复杂度为 $O(log_2N)$
对于一棵给定的 BST，某个待插入的值有且仅有唯一的插入位置（想一想，为什么），这个位置可以通过类似查找的过程确定，之后插入即可。

删除

BST 的删除比较复杂，分三类情况讨论：

• 要删除的为叶子节点，直接删除即可；
• 要删除的为链节点（即只有一棵非空子树），直接用非空子树的根节点代替自己即可；
• 要删除的节点有两棵非空子树，此时为了使删除后 BST 的性质仍然得到满足，一般选择后继节点（右子树中最小的节点）代替自己，当然也可以选择用前驱节点（左子树中最大的节点）。具体如何求不是本笔记的重点，此处略去。

理由：
若用子节点 $v$ 代替待删除的节点 $u$，则必须保证替换后仍然满足左子树中所有剩余节点 < $v$ < 右子树中所有剩余节点。
不难看出，如果要在左子树中取 $v$，则必须取左子树中最大的节点，否则左子树中存在至少一个节点 $k_1$ 满足 $k_1>v$，与 BST 的性质 1 矛盾。而又因为 $v$ < $u$ < 右子树中所有节点，显然 $v$ < 右子树中所有剩余节点一定成立。
类似地，如果要在右子树中取 $v$，则必须取右子树中最小的节点，否则右子树中存在至少一个节点 $k_2$，满足 $k_2<v$，与 BST 的性质 2 矛盾。因为左子树中所有节点 < $u$ < $v$，显然左子树中所有剩余节点 < $v$ 一定成立。
在编程实现中，我们默认初始时每个节点的左、右儿子均为空，则可以将情况 1 和 2 合并处理。而且在实现“替换”操作时，为了避免大量内存移动造成不必要的时间浪费，往往使用指针实现 BST。

现在来考虑关于重复节点的问题，一般有两种解决方案：一种方法我们规定把它插入左边， 另一种方法是我们在节点上再加一个域，记录重复节点的个数。如果采用后者，则删除的时候可以直接将记录节点个数的值减 1，当其值为 0 时才用上述的删除方法。

平衡性

那么，BST 的平衡性如何呢？
我们先来考虑时间复杂度问题。我们知道，在树的相关问题中，理想的情况下，链节点的个数应该尽量少，以避免树的退化。注意上面所提到的操作中，查找和插入都是期望时间复杂度为 $O(log_2N)$，也就意味着一旦出现退化，最坏情况（整棵树为一条链）将退化到 $O(N)$。
问题出在哪里呢？刚才提到，待插入的值有且仅有唯一的插入位置，也就意味着造成退化的不可能是插入，而应该是删除。
为什么会出现这种情况呢？原因在于删除时，我们总是选择将待删除节点的后继代替它本身。这样就会造成总是右边的节点数目减少，以至于树向左偏沉。
已经被证明，随机插入或删除 $N^2$ 次以后，树的期望深度为 $O(N^{\frac{1}{2}})$。我们可以在删除时随机地选择用前驱还是后继代替本身， 以消除向一边偏沉的问题。 这种神奇地做法消除了偏沉的不平衡，效果十分明显。
对待随机的数据 BST 已经做得很不错了， 但是有序的数据插入树中时，BST 还将不可避免地退化成一条链。这个时候，无论是查找、插入还是删除，都退化成了 $O(N)$ 的时间。

二、堆

堆包括二叉堆和多叉堆等，为了服务 Treap，这里只对其中的二叉堆（以下简称“堆”）作简要回顾。

定义

二叉堆 (binary heap) 是一棵满足如下性质的二叉树（为了方便，一般都是完全二叉树）：

• 父节点的键值总是小于或等于（大于或等于）任何一个子节点的键值。
• 每个节点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆(maximum heap，也常被译作“大根堆”)。当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆(minimum heap，也常被译作“小根堆”)。下图展示一个最小堆：

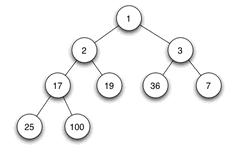
堆的维护（如插入、删除）都比较简单，且与 Treap 关联不大，因此这里不再赘述。如果有需要了解可以自行查阅相关资料。

为了解决 BST 的退化问题，各种自动平衡二叉查找树(Self-Balancing Binary Search Tree) 应运而生，接下来就进入正题，开始介绍 Treap。

三、Treap

什么是 Treap，为什么需要 Treap

Treap 是一种平衡树，可以认为是 BST 与堆的结合。事实上，它正是得名于 Tree + heap。
它和 BST 一样满足许多优美的性质，而引入堆目的就是为了维护平衡。下图是一棵 Treap，节点中黑色数值为键值，红色数值为修正值。

如何体现平衡

Treap 在 BST 的基础上，添加了修正值(fix)。当一个数被插入到 Treap 时，给它所在节点随机生成一个值作为修正值，它与节点的值无关，这使其平衡性得到了充分保证。在键值满足 BST 性质的基础上，Treap 节点的修正值还满足最小堆性质。于是，Treap 可定义为有以下性质的二叉树：

• 若其左子树不空， 则左子树上所有节点的值均小于其根节点的值， 而且其根节点的修正值小于等于左子树根节点的修正值；
• 若其右子树不空， 则右子树上所有节点的值均大于其根节点的值， 而且其根节点的修正值小于等于右子树根节点的修正值；
• 其左、右子树也分别为 Treap。

注意，修正值满足最大堆性质也是可以的，只需在维护堆性质时考虑相反的大小关系即可。为了方便，下面统一用最小堆性质描述。考虑到 Treap 要同时维护两种性质，且修正值是随机得到的，一般都会比较平衡，即使出了一点偏差也不会造成太严重的退化。从实际应用中来看，效果还是很不错的。

旋转

对 Treap 的维护基于旋转（rotate）操作，分为左旋和右旋。用一张图直观地感受 Treap 的旋转：

旋转的性质：

• 左旋一个子树，会把它的根节点旋转到根的左子树位置，原右子节点的左子节点成为根的右子节点，同时原右子节点成为子树的根；
• 右旋一个子树，会把它的根节点旋转到根的右子树位置，原左子节点的右子节点成为根的左子节点，同时原左子节点成为子树的根。

由上述描述中可以发现，左旋和右旋的操作具有对称性。这为我们在编程实现时简化代码提供了方便。
另外，不难直观地感受，对子树进行旋转并不会改变它的 BST 性质，下面就来说明这一点。

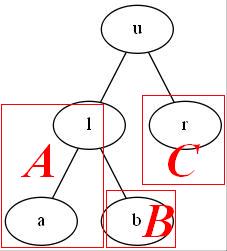
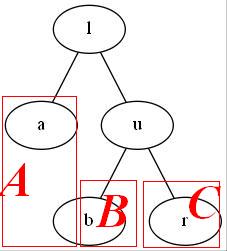
如上图，对左边的 Treap 进行右旋后变成了右边的形态。我们关注三棵子树：原左子节点 l 的左子树 $A$，$l$ 的右子树 $B$ 和原根节点 $u$ 的右子树 $C$。
首先，显而易见的是 $a$、$l$ 和 $u$ 之间关系仍然满足。在左图中是一条链，$a<l<u$，在右图中 $l$ 是根节点，$a$ 和 $u$ 分别为左右子节点，仍然满足 $a<l<u$。
接下来是对受到影响的三棵子树的讨论。对于子树 $A$，仍然是 $l$ 的左子树，不受影响，子树 $C$ 类似。对于子树 $B$，在左图中，它是 $u$ 的左子树的一部分，因此 $B$ 的所有节点小于 $u$，而它又是 $l$ 的右子树，因此 $B$ 的所有节点大于 $l$；可以发现在右图中它仍然满足 $l$<所有节点<$u$。
这样我们就证明了右旋并不会改变 BST 性质，而左旋的情况可以类似推理。

旋转对堆性质又有什么影响呢？还是以右旋为例进行说明，左旋同理。
借助上面的图，显然子树 $A$、$B$ 中的修正值均大于 $l$，没有受到改变，子树 $C$ 同理。注意虽然旋转导致了之前是祖先-后代关系的某些节点变成了兄弟（如 $a$ 和 $u$），但堆性质只需考虑与父节点的关系，因此实际上并没有造成影响。可以发现，修正值大小关系唯一改变的只有 $u$ 和 $l$ 之间的关系。

插入

Treap 的插入与 BST 类似，首先为待插入节点找到适当位置，之后给该节点赋一个随机修正值。之后就在返回的时候检查它的父节点与它的修正值关系，若它的修正值比父节点小则进行旋转以维护（左旋可将右子节点旋上来，右旋可将左子节点旋上来）。已经证明过旋转不会改变 BST 性质，而只调整与父节点之间的堆序，因此是正确的。注意旋转后可能仍然与其父节点不满足堆性质，则不断旋转，直至堆性质得到满足为止。这里不再具体举例。

删除

有了旋转操作，Treap 的删除比 BST 还要简单。由于删除叶子节点和删除链节点的情况与 BST 是一样的处理，这里只讨论有两个子节点的情况。
考察待删除节点的两个子节点，为了保证最小堆性质，应该将修正值较小的子节点调整为当前子树的根（如左子节点修正值较小则进行右旋），这样可以把要删除的节点转移下去，之后在待删除节点所被转移到的子树中继续讨论，直到节点可以直接被删除为止。

经过上面的概括总结，相信可以初步建立起对 Treap 的一些认识，其核心就在于旋转操作，不理解的话，可以自己画一些图，手动模拟一下。如果想要进一步学习 Treap，推荐参考资料 1 的论文。
而以 Treap 为代表的平衡树用途较广，可以实现相当多功能，如求第 k <script type="math/tex" id="MathJax-Element-1323">k</script> 大/小的数，求某个数的排名等，STL 中的 set 就是用红黑树实现的。
事实上，很多数据结构在经过合理的利用之后，都能发挥出意想不到的妙用。因此，正所谓“工欲善其事，必先利其器”，学习数据结构不能只流于背代码、写模板的表面，而应该在应用中逐步建立起对其的深刻认识，真正做到“为我所用”。

参考资料：

• 《随机平衡二叉查找树 Treap 的分析与应用》，清华大学计算机系 郭家宝(BYVoid)
• 《白话经典算法系列之七 堆与堆排序》，CSDN 博客 MoreWindows Blog