静电边值问题的唯一性定理

最新推荐文章于 2024-05-18 14:36:09 发布

东门之杨

最新推荐文章于 2024-05-18 14:36:09 发布

阅读量2.4k

点赞数 3

分类专栏：电动力学文章标签：电动力学静电场

本文链接：https://blog.csdn.net/u013795675/article/details/49024769

版权

电动力学专栏收录该内容

17 篇文章 1 订阅

订阅专栏

静电场

真空中的Maxwell方程

⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ \nabla \cdot E = ρ ε 0 \nabla \times E = - \partial B \partial t \nabla \cdot B = 0 \nabla \times B = μ 0 j + ε 0 μ 0 \partial E \partial t

$\begin{cases} \nabla\cdot\mathbf E=\dfrac{\rho}{\varepsilon_0}\\ \nabla\times\mathbf E=-\dfrac{\partial \mathbf B}{\partial t}\\ \nabla\cdot\mathbf B=0\\ \nabla\times\mathbf B=\mu_0\mathbf j+\varepsilon_0\mu_0\dfrac{\partial \mathbf E}{\partial t} \end{cases}$

在静电场中， $\dfrac{\partial \mathbf B}{\partial t}=0$ ，所以 $\nabla\times\mathbf E=0$ .
引入 $\phi$ ，使 $\mathbf E=-\nabla \phi$ ，代入第一个式子即得

\nabla 2 ϕ = - ρ ε 0

$\nabla^2\phi=-\dfrac{\rho}{\varepsilon_0}$
又因为

ϕ (x) = 1 4 π ε 0 \int ρ ( x ' ) | x - x ' | d x'

$\phi(\mathbf x)=\dfrac1{4\pi\varepsilon_0}\int\dfrac{\rho(\mathbf x')}{|\mathbf x-\mathbf x'|}\mathrm d\mathbf x'$
所以

\nabla 2 1 | x - x ' | = - 4 π δ (x - x')

$\nabla^2\dfrac{1}{|\mathbf x-\mathbf x'|}=-4\pi\delta(\mathbf x-\mathbf x')$

静电边值问题

问题：已知 $V$ 内 $\rho$ ，在什么条件下可以得到电场？
原则： $V$ 外的 $\rho$ 分布，都反映在边界上.因此只要再知道边界的条件即可得到电场.

设 $\psi,\phi$ 为任意的标量函数， $\mathbf c=\phi\nabla\psi$ ，由Gauss定理，

\int V \nabla \cdot c d τ = \oint c \cdot d α = \oint c \cdot n d α

$\int_V\nabla\cdot\mathbf c\mathrm d\tau=\oint\mathbf c\cdot\mathrm d\alpha=\oint\mathbf c\cdot \mathbf n\mathrm d\alpha$
得

\int V [ϕ \nabla 2 ψ + (\nabla ϕ) (\nabla ψ)] d τ = \oint ϕ \partial ψ \partial n d α

$\int_V[\phi\nabla^2\psi+(\nabla\phi)(\nabla\psi)]\mathrm d\tau=\oint\phi\dfrac{\partial \psi}{\partial n}\mathrm d\alpha$
把

ϕ,ψ $\phi,\psi$ 互换，得

\int V [ψ \nabla 2 ϕ + (\nabla ψ) (\nabla ϕ)] d τ = \oint ψ \partial ϕ \partial n d α

$\int_V[\psi\nabla^2\phi+(\nabla\psi)(\nabla\phi)]\mathrm d\tau=\oint\psi\dfrac{\partial \phi}{\partial n}\mathrm d\alpha$
两式相减，得

\int V (ϕ \nabla 2 ψ - ψ \nabla 2 ϕ) d τ = \oint (ϕ \partial ψ \partial n - ψ \partial ϕ \partial n) d α

$\int_V\left(\phi\nabla^2\psi-\psi\nabla^2\phi\right) \mathrm d\tau=\oint \left(\phi\dfrac{\partial \psi}{\partial n}-\psi\dfrac{\partial \phi}{\partial n}\right)\mathrm d\alpha$

取 $\phi=\phi(\mathbf x'),\psi=\dfrac1{|\mathbf x-\mathbf x'|}$
得到

\int V [- 4 π δ (x - x') ϕ (x') + 1 R ρ ( x ' ) ε 0] d 3 x' = \oint ⎛ ⎝ ⎜ ⎜ ϕ (x') \partial 1 R \partial n - 1 R \partial ϕ ( x ' ) \partial n ⎞ ⎠ ⎟ ⎟ d α

$\int_V\left[-4\pi\delta(\mathbf x-\mathbf x')\phi(\mathbf x')+\dfrac1{R}\dfrac{\rho(\mathbf x')}{\varepsilon_0}\right] \mathrm d^3\mathbf x'=\oint \left(\phi(\mathbf x')\dfrac{\partial \dfrac1{R}}{\partial n}-\dfrac1{R}\dfrac{\partial \phi(\mathbf x')}{\partial n}\right)\mathrm d\alpha$
所以有

ϕ (x') = 1 4 π ε 0 \int V ρ ( x ' ) R d 3 x' + 1 4 π \oint \partial V (1 R \partial ϕ ( x ' ) \partial n - ϕ (x') \partial \partial n 1 R) d α

$\phi(\mathbf x')=\dfrac1{4\pi\varepsilon_0}\int_V\dfrac{\rho(\mathbf x')}{R}\mathrm d^3\mathbf x'+\dfrac1{4\pi}\oint _{\partial V}\left(\dfrac1{R}\dfrac{\partial \phi(\mathbf x')}{\partial n}-\phi(\mathbf x')\dfrac{\partial }{\partial n}\dfrac1{R}\right)\mathrm d\alpha$
第二部分正是 边界对电场的影响.

唯一性定理

问题：什么样的边界条件可以唯一确定电场？
推导：两类边值条件都可以
设 $\Phi_1,\Phi_2$ 都是电场的解，定义 $U=\Phi_1-\Phi_2$ ，则

\nabla 2 U = 0

$\nabla^2U=0$

在

\int V [ϕ \nabla 2 ψ + (\nabla ϕ) (\nabla ψ)] d τ = \oint ϕ \partial ψ \partial n d α

$\int_V[\phi\nabla^2\psi+(\nabla\phi)(\nabla\psi)]\mathrm d\tau=\oint\phi\dfrac{\partial \psi}{\partial n}\mathrm d\alpha$
中，令

ϕ=ψ=U $\phi=\psi=U$ ，得

\int V [U \nabla 2 U + (\nabla U) 2] d τ = \oint U \partial U \partial n d α \Rightarrow \int V (\nabla U) 2 d τ = \oint \partial V U \partial U \partial n d α

$\int_V[U\nabla^2U+(\nabla U)^2]\mathrm d\tau=\oint U\dfrac{\partial U}{\partial n}\mathrm d\alpha\\\Rightarrow\int_V(\nabla U)^2\mathrm d\tau=\oint _{\partial V}U\dfrac{\partial U}{\partial n}\mathrm d\alpha$
因此，如果在边界处有

U = 0 o r \partial U \partial n = 0

$U=0\quad or\quad \dfrac{\partial U}{\partial n}=0$
那么

∇U=0 $\nabla U=0$ ，从而

Φ1,Φ2 $\Phi_1,\Phi_2$ 最多相差一个常数，在物理意义上是同一个函数.

即所求的边值条件是

Φ 1 = Φ 2 o r \partial Φ 1 \partial n = \partial Φ 2 \partial n

$\Phi_1=\Phi_2\quad or\quad \dfrac{\partial \Phi_1}{\partial n}=\dfrac{\partial \Phi_2}{\partial n}$ 或者说边界上的

ϕ $\phi$ 或

∂ϕ∂n $\dfrac{\partial \phi}{\partial n}$ 已知.

镜像法

镜像法：求解静电边值问题的一种方法.
依据：唯一性定理

例：镜像

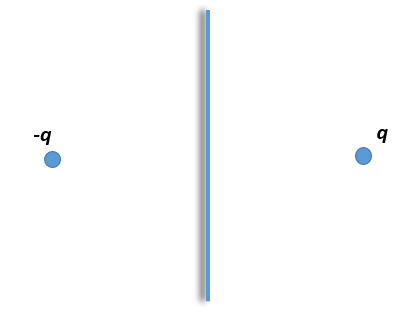
无限大的平面导体，距离平面 $a$ 处有一个电荷 $q$ ，求它引起的电势分布.

这里写图片描述

分析：

静电问题中的导体是一个等势体；
由于延伸到无穷远处，不妨设无穷远处的电势为 $0$ ，那么导体的电势处处为 $0$ .
左半平面的解是 $\varphi=0$
要研究右半平面的电势分布，已知内部电荷分布和边界电势分布即可，但是直接表示出电势分布并不方便；
采用镜像法，只需要在外部假设一个点电荷取代无限大边界，保证边值相同即可
这样的点电荷的取法即和 $q$ 位置对称、电荷为 $-q$ 的电荷.
采用镜像电荷，右半平面的电势可以方便写出
$φ (x, y, z) = 1 4 π ε q ( x - a ) 2 + y 2 + z 2 - - - - - - - - - - - - - - - \sqrt - 1 4 π ε q ( x + a ) 2 + y 2 + z 2 - - - - - - - - - - - - - - - \sqrt$ $\varphi(x,y,z)=\dfrac1{4\pi\varepsilon}\dfrac{q}{\sqrt{(x-a)^2+y^2+z^2}}-\dfrac1{4\pi\varepsilon}\dfrac{q}{\sqrt{(x+a)^2+y^2+z^2}}$
进而电场强度 $\mathbf E=-\nabla\varphi$ 也可以求出.

例：球面

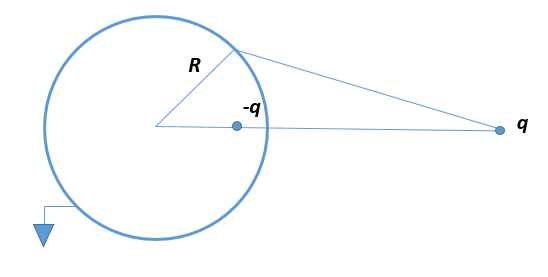
半径为 $R$ 的接地导体球，距离球心 $d>R$ 处有一个点电荷 $q$ ，求导体外的电势分布.

分析：

球面电势为0。
- 对所要研究的球外区域，其内部区域（球外）电荷分布已知，边界电势分布也已知（为 $0$ ），同样需要在外部区域（球内）找到一个电荷可以构造出同样的边界电势
- 其结论是该点的位置在 $q$ 的连心线上，满足
  $⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ a = R 2 b q' = - q R b$ $\begin{cases} a=\dfrac {R^2}b\\q'=-\dfrac{qR}{b} \end{cases}$
  因此，球外的电势分布可以方便地表示出(原点为圆心)
  $φ (x, y, z) = 1 4 π ε q ( x - b ) 2 + y 2 + z 2 - - - - - - - - - - - - - - \sqrt - 1 4 π ε q R b ( x - R 2 b ) 2 + y 2 + z 2 - - - - - - - - - - - - - - - - \sqrt$ $\varphi(x,y,z)=\dfrac1{4\pi\varepsilon}\dfrac{q}{\sqrt{(x-b)^2+y^2+z^2}}-\dfrac1{4\pi\varepsilon}\dfrac{qR}{b\sqrt{(x-\dfrac {R^2}b)^2+y^2+z^2}}$
- 拓展：
  1. 如果导体球不接地，但是已知球面的电势为定值 $\varphi_0$ ，那么采用叠加原理，在导体球内部再增加一个位于球心的点电荷，电荷量为 $4\pi\varepsilon R\varphi_0$
  2. 如果导体球不接地，但是已知球面的电荷量为 $Q$ ，同样采用叠加原理，在球心增加一个点电荷？
  格林函数法
  
  ∇′2G(x,x′)=−4πδ(x−x′)G(x,x′)=1|x−x′|+F(x,x′)∇′2F(x,x′)=0
  
  对已知 Φ 在边界值（第一类边界条件），通过适当选取 F ，使GD(x,x′)=0 for x′ 在边界。从而有
  
  Φ(x)=14πε0∫VρGD+14π∮(−1)Φ∂G′D∂n′（形式解）
  
  即第一类格林函数 GD
  
  {∇′2GD(x,x′)=−4πδ(x−x′)GD(x,x′)=0(∂V)
  
  对第二类边界条件，理想的是
  
  ⎧⎩⎨∇′2GN(x,x′)=−4πδ(x−x′)∂∂n′GN(x,x′)=0(∂V)
  
  但是由于Gauss定理
  
  ∮∂V(∂G′∂n′)⋅dα=4π≠0
  
  所以只能取
  
  ∂∂n′GN(x,x′)=−4πS
  
  电势分布的形式解为
  
  Φ(x)=14πε0∫ρGN+14π∮GN(∂ϕ∂n′)+⟨Φ⟩S
  
  特解叠加法
  
  形式
  
  Φ(x)=∑n∫fn(x)Cn
  
  原则
  1. 把 $\rho$ 分开
  2. 根据边界形状定 $f_n(\mathbf x)$
  ∇2Φ=−ρε0Φ=ϕc+ϕ⎧⎩⎨ϕc=14πε0∫VρRdτ∇2ϕ=0
  
  $\nabla^2\phi=0$ 在球坐标下分离变量
  
  分离变量的结果是
  
  ⎧⎩⎨Q=e±imφU=Arl+1+Br−lPml(x)=连带勒让德函数,x=cosθ
  
  特殊情形：方位角对称， m=0 .
  
  ϕ(r,θ)=∑l=0∞(Alrl+Blr−l+1Pl(cosθ),Al,Bl对称
  
  例
  
  半径为 $a$ 的球，球面电势
  U=⎧⎩⎨⎪⎪V,0<θ<π2−V,π2≤θ<π
  
  求球内外电势.
  
  Thanks to Mr. Zhu