代码:
#include<iostream>
#include<vector>
#include<stack>
using namespace std;
template<typename T>
struct binaryTreeNode{
T element;
binaryTreeNode<T> *leftChild; //左子树
binaryTreeNode<T> *rightChild; //右子树
binaryTreeNode() {
leftChild = rightChild = NULL;
}
binaryTreeNode(const T& theElement)
{
element = theElement;
leftChild = rightChild = NULL;
}
binaryTreeNode(const T& theElement, binaryTreeNode *theLeftChild, binaryTreeNode *theRightChild)
{
element(theElement);
leftChild = theLeftChild;
rightChild = theRightChild;
}
};
template <typename T>
class binaryTree{
public:
virtual ~binaryTree() {}
virtual bool empty() const = 0;
virtual int size() const = 0;
virtual void visit(T *) const = 0;
virtual void InputBinaryNode() = 0;
virtual void preCreateBinaryTree(T *&) = 0;
/*virtual void preOrder(binaryTreeNode<T> *node) = 0;
virtual void inOrder(binaryTreeNode<T> *node) = 0;
virtual void postOrder(binaryTreeNode<T> *node) = 0;
virtual void Iter_preOrder(binaryTreeNode<T> *node) = 0;
virtual void Iter_inOrder(binaryTreeNode<T> *node) = 0;
virtual void Iter_postOrder(binaryTreeNode<T> *node) = 0;*/
virtual void preOrder(T *) = 0;
virtual void inOrder(T *) = 0;
virtual void postOrder(T *) = 0;
virtual void Iter_preOrder(T *) = 0;
virtual void Iter_inOrder(T *) = 0;
virtual void Iter_postOrder(T *) = 0;
};
template<typename E>
class linkedBinaryTree : public binaryTree<binaryTreeNode<E> >
{
public:
linkedBinaryTree(){ root = NULL; treeSize = 0; }
~linkedBinaryTree() {};
bool empty() const { return treeSize == 0; }
int size() const { return treeSize; }
void visit(binaryTreeNode<E> *node) const;
void InputBinaryNode();
void preCreateBinaryTree(binaryTreeNode<E> *&node);
int height(binaryTreeNode<E> *&node) const;
void preOrder(binaryTreeNode<E> *node);
void inOrder(binaryTreeNode<E> *node);
void postOrder(binaryTreeNode<E> *node);
void Iter_preOrder(binaryTreeNode<E> *node);
void Iter_inOrder(binaryTreeNode<E> *node);
void Iter_postOrder(binaryTreeNode<E> *node);
private:
binaryTreeNode<E> *root;
int treeSize;
vector<E> vecNode;
};
template<typename E>
void linkedBinaryTree<E>::visit(binaryTreeNode<E> *node) const
{
//访问节点*node, 仅输出element
cout << node->element << " ";
}
template<typename E>
void linkedBinaryTree<E>::InputBinaryNode()
{
E elem;
cout << "!!!注意:(1)#表示空节点;(2)请在输入的字符串末尾加0,作为输入结束的标志!" << endl;
while (cin >> elem && elem != '0')
{
vecNode.push_back(elem);
}
}
template<typename E>
void linkedBinaryTree<E>::preCreateBinaryTree(binaryTreeNode<E> *&node)
{
vector<E>::iterator it = vecNode.begin();
if (it != vecNode.end())
{
if (*it == '#')
{
node = NULL;
vecNode.erase(it);
}
else{
node = new binaryTreeNode<E>(*it); //生成根节点
treeSize++;
vecNode.erase(it);
preCreateBinaryTree(node->leftChild); //构造左子树
preCreateBinaryTree(node->rightChild); //构造右子树
}
}
else{
node = NULL;
}
}
template<typename E>
int linkedBinaryTree<E>::height(binaryTreeNode<E> *&node) const
{
if (!node)
{
return 0;
}
int hl = height(node->leftChild); //左子树的高
int hr = height(node->rightChild); //右子树的高
if (hl > hr)
{
return ++hl;
}
else{
return ++hr;
}
}
template<typename E>
void linkedBinaryTree<E>::preOrder(binaryTreeNode<E> *node)
{
//根节点——左子树——右子树
if (node)
{
visit(node);
preOrder(node->leftChild);
preOrder(node->rightChild);
}
}
template<typename E>
void linkedBinaryTree<E>::inOrder(binaryTreeNode<E> *node)
{
//左子树——根节点——右子树
if (node)
{
inOrder(node->leftChild);
visit(node);
inOrder(node->rightChild);
}
}
template<typename E>
void linkedBinaryTree<E>::postOrder(binaryTreeNode<E> *node)
{
//左子树——右子树——根节点
if (node)
{
postOrder(node->leftChild);
postOrder(node->rightChild);
visit(node);
}
}
template<typename E>
void linkedBinaryTree<E>::Iter_preOrder(binaryTreeNode<E> *node)
{
stack<binaryTreeNode<E>* > stk; //存储树节点
binaryTreeNode<E> * currNode = node;
while (currNode || (!stk.empty()))
{
if (currNode)
{
visit(currNode); //访问根节点
stk.push(currNode);
currNode = currNode->leftChild; //遍历左子树
}
else{
currNode = stk.top(); //节点入栈前已被访问,故无需再次访问
stk.pop();
currNode = currNode->rightChild;
}
}
}
template<typename E>
void linkedBinaryTree<E>::Iter_inOrder(binaryTreeNode<E> *node)
{
stack<binaryTreeNode<E>* > stk;
binaryTreeNode<E>* currNode = node;
while (currNode || (!stk.empty()))
{
if (currNode)
{
stk.push(currNode); //先将左子树全部压入栈
currNode = currNode->leftChild;
}
else{
currNode = stk.top();
stk.pop();
visit(currNode); //访问根节点
currNode = currNode->rightChild;
}
}
}
template<typename E>
void linkedBinaryTree<E>::Iter_postOrder(binaryTreeNode<E> *node)
{
stack<binaryTreeNode<E>* > stk;
binaryTreeNode<E>* currNode = node, *rightNode = node;
while (currNode || (!stk.empty()))
{
if (currNode)
{
stk.push(currNode); //遍历左子树
currNode = currNode->leftChild;
}
else{
currNode = stk.top();
currNode = currNode->rightChild; //遍历右子树
if (!currNode) //此时栈顶元素的左孩子、右孩子均为空,即为叶子节点
{
rightNode = stk.top();
stk.pop();
visit(rightNode); //访问叶子节点
//若刚被访问的叶子节点是此时栈顶元素的右孩子,则说明左、右子树均被遍历完
//循环的目的是为了找到最终的父结点,当前所有已访问的节点是作为其左子树的节点而存在
while ((!stk.empty()) && (stk.top()->rightChild == rightNode))
{
rightNode = stk.top(); //由于该节点的右节点已被访问,说明完成了左右子树的遍历
stk.pop();
visit(rightNode); //叶子节点已经被访问,则最后访问根节点
}
if (!stk.empty()) //刚被访问的是此时栈顶元素的左孩子,则右孩子还未入栈
{
currNode = stk.top();
currNode = currNode->rightChild;
}
}
}//else
}
}
int main(int argc, char* argv[])
{
linkedBinaryTree<char> LBT;
binaryTreeNode<char>* root;
LBT.InputBinaryNode();
LBT.preCreateBinaryTree(root);
cout << "二叉树的总节点数为:" << LBT.size() << endl;
cout << "二叉树的高度为:"<< LBT.height(root) << endl;
cout << "\n前序遍历二叉树(递归):" << endl;
LBT.preOrder(root);
cout << "\n中序遍历二叉树(递归):" << endl;
LBT.inOrder(root);
cout << "\n后序遍历二叉树(递归):" << endl;
LBT.postOrder(root);
cout << "\n\n前序遍历二叉树(非递归):" << endl;
LBT.Iter_preOrder(root);
cout << "\n中序遍历二叉树(非递归):" << endl;
LBT.Iter_inOrder(root);
cout << "\n后序遍历二叉树(非递归):" << endl;
LBT.Iter_postOrder(root);
return 0;
}注:中间注释代码部分会造成,纯虚函数没有强制替代项的错误。
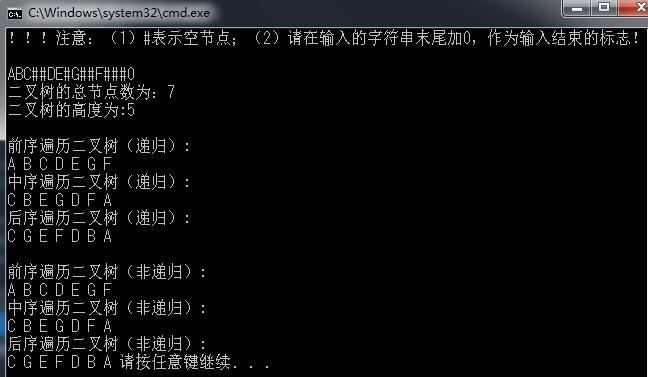
结果 :
注:上述代码是在我的旧文基础上改进的http://blog.csdn.net/u014033518/article/details/38844583






















 3725
3725

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








