支持向量机入门系列-2：等式约束极小的最优性条件

 

对支持向量机的求解都是将上节说的原问题转化为对偶问题进行求解的，这些内容都是最优化课程中的内容。

 

回忆上节的内容，我们的目标是寻找函数在若干约束条件下的最小值。在上节的原问题中，约束条件是包含不等式的，本节先考虑简单的问题，即考虑只包含等式约束的最优化问题：

                               （1）

其中f(x)被称作目标函数，而下面是一系列的等式约束。回想一下，当没有任何约束存在的时候，应该怎样寻找最优点呢？事实上x^*是最优点的必要条件是：

  

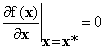
而如果函数f(x)是凸函数的话，这个条件也是充分条件（关于凸函数，请参考维基百科）。

 

插入一个说明，如果函数f(x)是一个实值函数，x是一个n维向量，那么f(x)对向量x的导数被定义为&