各种基本算法实现小结

最新推荐文章于 2022-03-20 22:26:58 发布
最新推荐文章于 2022-03-20 22:26:58 发布
阅读量2k 收藏 3
点赞数 1
分类专栏： 算法学习 文章标签： 算法 null struct graph output insert

（此贴转自 阳光岛主 ，仅做收藏之用，在此谢谢啦！）

 

单链表(测试通过)   

测试环境： Win-TC

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>  
  2. struct _node  
  3. {  
  4.     int data;  
  5.     struct _node *next;  
  6. };  
  7. typedef struct _node list;  
  8. void display(list *l)  
  9. {  
  10.     list *p;  
  11.     p=l;  
  12.     while(p->next)  
  13.     {  
  14.         printf("%5d", p->next->data);  
  15.         p=p->next;  
  16.     }  
  17. }  
  18. void main()  
  19. {  
  20.     int i, n;  
  21.     list *h, *p, *s;  
  22.     printf("Enter num n:");  
  23.     scanf("%d", &n);  
  24.     h=(list*)malloc(sizeof(list));  
  25.     h->data=-1;  
  26.     h->next=NULL;  
  27.     s=p=h;  
  28.     for(i=n;i>0;i--)  
  29.     {  
  30.         p=(list*)malloc(sizeof(list));  
  31.         scanf("%d", &(p->data));  
  32.         p->next=h->next;  
  33.         h->next=p;  
  34.         h=h->next;  
  35.     }  
  36.     display(s);  
  37.     getch();  
  38. }  

运行结果：


=================================================

单链表各种操作(测试通过)    

测试环境： Win-TC

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <malloc.h>   
  3. #include <stdlib.h>   
  4. struct  _node  
  5. {  
  6.     int  data;  
  7.     struct  _node *next;  
  8. };  
  9. typedef   struct  _node node, *plist;  
  10. plist init_list()  
  11. {  
  12.     plist pl;  
  13.     pl=(plist)malloc(sizeof (node));  
  14.     if (NULL==pl)  
  15.     {  
  16.         printf("init list,  malloc is fail.../n" );  
  17.         return  NULL;  
  18.     }  
  19.     pl->data=-1;  
  20.     pl->next=NULL;  
  21.     return  pl;  
  22. }  
  23. int  isempty_list(plist pl)  
  24. {  
  25.     if (NULL==pl || NULL!=pl->next)  
  26.         return  1;  
  27.     else   
  28.         return  0;  
  29. }  
  30. plist clear_list(plist pl)  
  31. {  
  32.     pl=NULL;  
  33.     return  pl;  
  34. }  
  35. void  destroy_list(plist pl)  
  36. {  
  37.     plist p, s;  
  38.       
  39.     p=pl->next;  
  40.     while (p)  
  41.     {  
  42.         s=p;  
  43.         p=p->next;  
  44.         free(s);       
  45.     }  
  46.       
  47.     pl=NULL;  
  48. }  
  49. void  insert_item(plist pl,  int  i,  int  e)  
  50. {  
  51.     int  j=1;  
  52.     plist p, s;  
  53.     p=pl;  
  54.     while (p && j<i)  
  55.     {  
  56.         p=p->next;  
  57.         j++;  
  58.     }  
  59.     if (!p || j>i)   /* >len or <1  */   
  60.         printf("Insert fail.../n" );  
  61.     s=(plist)malloc(sizeof (node));  
  62.     s->data=e;  
  63.     s->next=p->next;  
  64.     p->next=s;  
  65. }  
  66. void  display(plist pl)  
  67. {  
  68.     plist p;  
  69.     p=pl->next;  
  70.     while (pl && p)  
  71.     {  
  72.         printf("%5d" , p->data);  
  73.         p=p->next;  
  74.     }  
  75.     printf("/n/n" );  
  76. }  
  77. int  getbyid_item(plist pl,  int  i)  
  78. {  
  79.     plist p=pl->next;  
  80.     int  j=1;  
  81.     while (p && j<i)  
  82.     {  
  83.         p=p->next;  
  84.         j++;  
  85.     }  
  86.     if (!p || j>i)   /* >len or <1  */   
  87.     {  
  88.         printf("fail.../n" );  
  89.         exit(1);  
  90.     }  
  91.     return  p->data;  
  92. }  
  93. int  locate_item(plist pl,  int  e)  
  94. {  
  95.     plist p=pl->next;  
  96.     int  j=1;  
  97.     while (p->data != e && p->next)  
  98.     {  
  99.         p=p->next;  
  100.         j++;  
  101.     }  
  102.     if (p->data == e)  
  103.         return  j;  
  104.     else   
  105.     {  
  106.         printf("There is n %d in list/n" , e);  
  107.         return  -1;  
  108.     }  
  109. }  
  110. void  delete_item(plist pl,  int  i,  int  *e)  
  111. {  
  112.     plist p=pl;  
  113.     plist q;  
  114.     int  j=1;  
  115.     while (p->next && j<i)  
  116.     {  
  117.         p=p->next;  
  118.         j++;  
  119.     }  
  120.     if (!p->next || j>i)   /* >len or <1  */   
  121.     {  
  122.         printf("fail..../n" );  
  123.         return ;  
  124.     }  
  125.     q=p->next;  
  126.     p->next=q->next;  
  127.     *e=q->data;  
  128.     free(q);  
  129. }  
  130. int  len_list(plist pl)  
  131. {  
  132.     int  j=0;  
  133.     plist p=pl;  
  134.     while (pl && p->next)  
  135.     {  
  136.         j++;  
  137.         p=p->next;  
  138.     }  
  139.     return  j;  
  140. }  
  141. plist traverse_list(plist pl)  
  142. {  
  143.     plist h, p, s;  
  144.       
  145.     if (!pl || !pl->next)  
  146.         return  pl;  
  147.     h=pl->next;  
  148.     s=h;  
  149.     p=s->next;  
  150.     h->next=NULL;  
  151.     while (p)  
  152.     {  
  153.         s=p;  
  154.         p=p->next;  
  155.         s->next=h;  
  156.         h=s;  
  157.     }  
  158.     pl->next=h;  
  159.       
  160.     return  pl;  
  161. }  
  162. void  main()  
  163. {  
  164.     int  len, pos, *del;  
  165.     plist pl=NULL;  
  166.     del=(int  *)malloc( sizeof ( int ));  
  167.     pl=init_list();  
  168.     isempty_list(pl);  
  169.     insert_item(pl, 1, 1);  
  170.     insert_item(pl, 2, 3);  
  171.     insert_item(pl, 3, 5);  
  172.     insert_item(pl, 4, 7);  
  173.     insert_item(pl, 5, 9);  
  174.     insert_item(pl, 6, 11);  
  175.     display(pl);  
  176.     len=len_list(pl);  
  177.     printf("link list len: %d/n" , len);  
  178.     pos=locate_item(pl, 7);  
  179.     printf("num 7 pos: %d/n" , pos);  
  180.     delete_item(pl, 3, del);  
  181.     printf("delete pos 3 num: %d/n" , *del);  
  182.     display(pl);  
  183.     printf("link list traverse.../n" );  
  184.     pl=traverse_list(pl);  
  185.     display(pl);  
  186.     destroy_list(pl);  
  187.     getch();  
  188. }  

运行结果：


=================================================

单向循环链表(测试通过)    

测试环境： Win-TC

·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <malloc.h>   
  3. struct  _node  
  4. {  
  5.     int  data;  
  6.     struct  _node *next;  
  7. };  
  8. typedef   struct  _node node, *plist;  
  9. plist init_list()  
  10. {  
  11.     plist pl=(plist)malloc(sizeof (node));  
  12.     if (!pl)  
  13.     {  
  14.         printf("error malloc fail.../n" );  
  15.         return  NULL;  
  16.     }  
  17.     pl->data=-1;  
  18.     pl->next=pl;    /* pl->next=NULL */   
  19.     return  pl;  
  20. }  
  21. void  insert_item(plist pl,  int  pos,  int  data)  
  22. {  
  23.     int  j=0;  
  24.     plist p,s;  
  25.     s=p=pl;  
  26.     while (p && j<pos-1)  
  27.     {  
  28.         p=p->next;  
  29.         j++;  
  30.     }  
  31.     if (!p || j>pos-1)  
  32.     {  
  33.         printf("Error insert fail.../n" );  
  34.         return ;  
  35.     }  
  36.     s=(plist)malloc(sizeof (node));  
  37.     if (!s)  
  38.     {  
  39.         printf("Error malloc fail.../n" );  
  40.         return ;  
  41.     }  
  42.     s->data=data;  
  43.     s->next=p->next;  
  44.     p->next=s;  
  45. }  
  46. int  find_item(plist pl,  int  data)  
  47. {  
  48.     plist s,p;  
  49.     s=p=pl;  
  50.     p=p->next;  
  51.     while (s != p)  
  52.     {  
  53.         if (data==p->data)  
  54.             return  1;  
  55.         p=p->next;  
  56.     }  
  57.     return  0;  
  58. }  
  59. void  delete_item(plist pl,  int  data)  
  60. {  
  61.     plist p,s;  
  62.     s=p=pl;  
  63.     if (data == p->data)  /* first item is equal with data, then last item = second item */   
  64.     {  
  65.         s=p;  
  66.         while (s != p->next)  
  67.             p=p->next;  
  68.         p->next=s->next;  
  69.         return ;  
  70.     }  
  71.     while (s != p->next)  /* first item is not equal with data */   
  72.     {  
  73.         if (data == p->next->data)  
  74.         {  
  75.             p->next=p->next->next;  
  76.             return ;  
  77.         }  
  78.         p=p->next;  
  79.     }  
  80. }  
  81. void  display(plist pl)  
  82. {  
  83.     plist s,p;  
  84.     s=p=pl;  
  85.     printf("%5d" , p->data);  /* print first item */   
  86.     p=p->next;  
  87.     while (s != p)  
  88.     {  
  89.         printf("%5d" , p->data);  
  90.         p=p->next;  
  91.     }  
  92.     printf("/n/n" );  
  93. }  
  94. void  main()  
  95. {  
  96.     int  f;  
  97.     plist pl;  
  98.     pl=init_list();  
  99.     insert_item(pl, 1, 1);  
  100.     insert_item(pl, 2, 3);  
  101.     insert_item(pl, 3, 5);  
  102.     insert_item(pl, 4, 7);  
  103.     insert_item(pl, 5, 9);  
  104.     display(pl);  
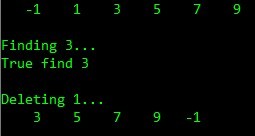
  105.     printf("Finding 3.../n" );  
  106.     f=find_item(pl, 3);  
  107.     if (f)  
  108.         printf("True find 3/n" );  
  109.     else   
  110.         printf("False find 3.../n" );  
  111.     printf("/nDeleting 1.../n" );  
  112.     delete_item(pl->next, 1);  
  113.     display(pl->next);  
  114.     getch();  
  115. }  

运行结果：

 
=================================================

双向循环链表(测试通过)    

测试环境： Win-TC

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <malloc.h>   
  3. struct  _node  
  4. {  
  5.     int  data;  
  6.     struct  _node *prior;  
  7.     struct  _node *next;  
  8. };  
  9. typedef   struct  _node node, *plist;  
  10. plist init_list()  
  11. {  
  12.     plist p;  
  13.     p=(plist)malloc(sizeof (node));  
  14.     if (!p)  
  15.     {  
  16.         printf("Error, malloc fail.../n" );  
  17.         return  NULL;  
  18.     }  
  19.     p->data=-1;   /* head->data = -1 */   
  20.     p->prior=p;  
  21.     p->next=p;  
  22.     return  p;  
  23. }  
  24. void  insert_item(plist pl,  int  pos,  int  data)  
  25. {  
  26.     int  j=0;  
  27.     plist s,p;  
  28.     p=pl;  
  29.     while (p && j<pos-1)  
  30.     {  
  31.         p=p->next;  
  32.         j++;  
  33.     }  
  34.     if (!p || j>pos-1)  /* pos is less than 1 or pos larger than len_list+1 */   
  35.     {  
  36.         printf("Error %d is invalide num.../n" , pos);  
  37.         return ;  
  38.     }  
  39.     s=(plist)malloc(sizeof (node));  
  40.     if (!s)  
  41.     {  
  42.         printf("Error, malloc fail.../n" );  
  43.         return  NULL;  
  44.     }  
  45.     s->data=data;  
  46.     s->prior=p;  
  47.     s->next=p->next;  
  48.     p->next->prior=s;  
  49.     p->next=s;  
  50. }  
  51. int  find_item(plist pl,  int  data)  
  52. {  
  53.     plist s,p;  
  54.     s=p=pl;  
  55.     if (data == p->data)  
  56.         return  1;  
  57.     p=p->next;  
  58.     while (s != p)  
  59.     {  
  60.         if (data == p->data)  
  61.             return  1;  
  62.         p=p->next;  
  63.     }  
  64.     return  0;  
  65. }  
  66. void  delete_item(plist pl,  int  data)  
  67. {  
  68.     plist s,p;  
  69.     s=p=pl;  
  70.     if (data == p->data)  /* first check equal */   
  71.     {  
  72.         p->prior->next=p->next;  
  73.         p->next=p->prior;  
  74.         return ;  
  75.     }  
  76.     while (s != p->next)  
  77.     {  
  78.         if (data == p->next->data)  
  79.         {  
  80.             p->next=p->next->next;  
  81.             p->next->next->prior=p;  
  82.         }  
  83.         p=p->next;  
  84.     }  
  85. }  
  86. void  display(plist pl)  
  87. {  
  88.     plist s,p;  
  89.     s=p=pl;  
  90.     printf("%5d" , p->data);   /* first item, such as head->data is -1 */   
  91.     p=p->next;  
  92.     while (s != p)  
  93.     {  
  94.         printf("%5d" , p->data);  
  95.         p=p->next;  
  96.     }  
  97.     printf("/n/n" );  
  98. }  
  99. void  main()  
  100. {  
  101.     int  f;  
  102.     plist pl;  
  103.     pl=init_list();  
  104.     insert_item(pl, 1, 1);  
  105.     insert_item(pl, 2, 3);  
  106.     insert_item(pl, 3, 5);  
  107.     insert_item(pl, 4, 7);  
  108.     insert_item(pl, 5, 9);  
  109.     display(pl);  
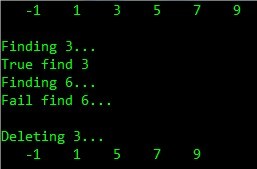
  110.     printf("Finding 3.../n" );  
  111.     f=find_item(pl->next->next, 3);  
  112.     if (f)  
  113.         printf("True find 3/n" );  
  114.     else   
  115.         printf("Fail find 3.../n" );  
  116.     printf("Finding 6.../n" );  
  117.     f=find_item(pl->prior->prior, 6);  
  118.     if (f)  
  119.         printf("True find 6/n" );  
  120.     else   
  121.         printf("Fail find 6.../n" );  
  122.     printf("/nDeleting 3.../n" );  
  123.     delete_item(pl->next->next, 3);  
  124.     display(pl);  
  125.     getch();  
  126. }  
运行结果：

======================================================

 

各种基本算法实现小结（二）—— 堆 栈

（均已测试通过）

==============================================================

栈——数组实现

测试环境：Win - TC

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. char  stack[512];  
  3. int  top=0;  
  4. void  push( char  c)  
  5. {  
  6.     stack[top]=c;  
  7.     top++;  
  8. }  
  9. char  pop()  
  10. {  
  11.     top--;  
  12.     return  stack[top];  
  13. }  
  14. int  is_empty()  
  15. {  
  16.     return  0==top;  
  17. }  
  18. void  main()  
  19. {  
  20.     push('1' );  
  21.     push('2' );  
  22.     push('3' );  
  23.     push('4' );  
  24.     push('5' );  
  25.     while (!is_empty())  
  26.         putchar(pop());  
  27.     putchar('/n' );  
  28.     getch();  
  29. }  

运行结果：

====================================================

栈 ——数组实现2

测试环境：Win - TC

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <malloc.h>   
  3. /* typedef int DataType; */   
  4. #define DataType int   
  5. #define MAX 1024   
  6. typedef   struct   
  7. {  
  8.     DataType data[MAX];  
  9.     int  top;  
  10. }stack, *pstack;  
  11. pstack *init_stack()  
  12. {  
  13.     pstack ps;  
  14.     ps=(pstack)malloc(sizeof (stack));  
  15.     if (!ps)  
  16.     {  
  17.         printf("Error. fail malloc.../n" );  
  18.         return  NULL;  
  19.     }  
  20.     ps->top=-1;  
  21.     return  ps;  
  22. }  
  23. int  empty_stack(pstack ps)  
  24. {  
  25.     if (-1 == ps->top)  
  26.         return  1;  
  27.     else   
  28.         return  0;  
  29. }  
  30. int  push(pstack ps, DataType data)  
  31. {  
  32.     if (ps->top == MAX-1)  
  33.     {  
  34.         printf("Stack is full.../n" );  
  35.         return  0;  
  36.     }  
  37.     ps->top++;  
  38.     ps->data[ps->top]=data;  
  39.     return  1;  
  40. }  
  41. int  pop(pstack ps, DataType *data)  
  42. {  
  43.     if (empty_stack(ps))  
  44.     {  
  45.         printf("Stack is empty.../n" );  
  46.         return  0;  
  47.     }  
  48.     *data=ps->data[ps->top];  
  49.     ps->top--;  
  50.     return  1;  
  51. }  
  52. DataType top_stack(pstack ps)  
  53. {  
  54.     if (empty_stack(ps))  
  55.     {  
  56.         printf("Stack is empty.../n" );  
  57.         return  0;  
  58.     }  
  59.     return  ps->data[ps->top];  
  60. }  
  61. void  display(pstack ps)  
  62. {  
  63.     int  i;  
  64.     if (empty_stack(ps))  
  65.     {  
  66.         printf("Stack is empty.../n" );  
  67.         return ;  
  68.     }  
  69.     printf("printf the items of stack.../n" );  
  70.     for (i=ps->top;i>-1;i--)  
  71.         printf("%4d" , ps->data[i]);  
  72.     printf("/n/n" );  
  73. }  
  74. void  main()  
  75. {  
  76.     int  i, num, data, *pdata;  
  77.     pstack ps;  
  78.     ps=init_stack();  
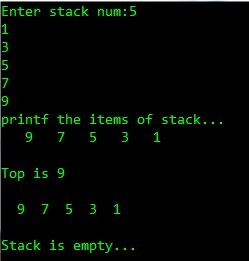
  79.     printf("Enter stack num:" );  
  80.     scanf("%d" , &num);  
  81.     for (i=0;i<num;i++)  
  82.     {  
  83.         scanf("%d" , &data);  
  84.         push(ps, data);  
  85.     }  
  86.     display(ps);  
  87.     printf("Top is %d/n/n" , top_stack(ps));  
  88.     for (i=0;i<num;i++)  
  89.     {  
  90.         pop(ps, pdata);  
  91.         printf("%3d" , *pdata);  
  92.     }  
  93.     printf("/n/n" );  
  94.     display(ps);  
  95.     getch();  
  96. }  

运行结果：

====================================================

栈 ——链表实现

测试环境：Win - TC

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <malloc.h>   
  3. typedef   char  DataType;  
  4. struct  _node  
  5. {  
  6.     DataType data;  
  7.     struct  _node *next;  
  8. };  
  9. typedef   struct  _node node, *pstack;  
  10. pstack init_stack()  
  11. {  
  12.     pstack ps;  
  13.     ps=(pstack)malloc(sizeof (node));  
  14.     if (NULL == ps)  
  15.     {  
  16.         printf("Error. malloc is fail.../n" );  
  17.         return  NULL;  
  18.     }  
  19.     ps->data=-1;  /* base of stack: data=-1 and next=NULL */   
  20.     ps->next=NULL;  
  21.     return  ps;  
  22. }  
  23. pstack push(pstack ps, DataType data)  
  24. {  
  25.     pstack ptop;  
  26.     ptop=(pstack)malloc(sizeof (node));  
  27.     if (NULL == ptop)  
  28.     {  
  29.         printf("Error. malloc is fail.../n" );  
  30.         return  NULL;  
  31.     }  
  32.     ptop->data=data;  
  33.     ptop->next=ps;   /* insert new item */   
  34.     ps=ptop;         /* move top */   
  35.     return  ps;  
  36. }  
  37. pstack pop(pstack ps, DataType *data)  
  38. {  
  39.     if (ps->next == NULL)  
  40.     {  
  41.         printf("stack is empty.../n" );  
  42.         return  NULL;              
  43.     }  
  44.     *data=ps->data;  
  45.     ps=ps->next;  
  46.     return  ps;  
  47. }  
  48. DataType top_stack(pstack ps)  
  49. {  
  50.     if (ps->next == NULL)   /* if empty */   
  51.     {  
  52.         printf("stack is empty.../n" );  
  53.         return  -1;  
  54.     }  
  55.     return  ps->data;  
  56. }  
  57. int  len_stack(pstack ps)  
  58. {  
  59.     int  len=0;  
  60.     pstack ptop=ps;  
  61.     while (ptop->next)  
  62.     {  
  63.         len++;  
  64.         ptop=ptop->next;  
  65.     }  
  66.     return  len;  
  67. }  
  68. void  display(pstack ps)  
  69. {  
  70.     pstack ptop;  
  71.     ptop=ps;  
  72.     while (ptop->next != NULL)  
  73.     {  
  74.         printf("%4c" , ptop->data);  
  75.         ptop=ptop->next;  
  76.     }  
  77.     printf("/n/n" );  
  78. }  
  79. void  main()  
  80. {  
  81.     pstack ps;  
  82.     DataType *data=(DataType *)malloc(sizeof (DataType));  
  83.     ps=init_stack();  
  84.     ps=push(ps, 'a' );  
  85.     ps=push(ps, 'b' );  
  86.     ps=push(ps, 'c' );  
  87.     ps=push(ps, 'd' );  
  88.     ps=push(ps, 'e' );  
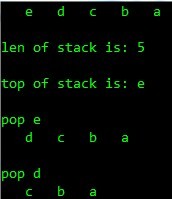
  89.     display(ps);  
  90.     printf("len of stack is: %d/n/n" , len_stack(ps));  
  91.     printf("top of stack is: %c/n/n" , top_stack(ps));  
  92.     ps=pop(ps, data);  
  93.     printf("pop %c/n" ,*data);  
  94.     display(ps);  
  95.     ps=pop(ps, data);  
  96.     printf("pop %c/n" ,*data);  
  97.     display(ps);  
  98.     getch();  
  99. }  

运行结果：

========================================================

堆 ——链表实现

测试环境：Win - TC

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <malloc.h>   
  3. #include <stdlib.h>   
  4. struct  _node  
  5. {  
  6.     int  data;  
  7.     struct  _node *next;  
  8. };  
  9. typedef   struct  _node node, *pnode;  
  10. struct  _linkqueue  
  11. {  
  12.     pnode front;  
  13.     pnode rear;      
  14. };  
  15. typedef   struct  _linkqueue linkqueue, *plinkqueue;  
  16. linkqueue init_queue()  
  17. {  
  18.     linkqueue lq;  
  19.     lq.front=lq.rear=(pnode)malloc(sizeof (node));  
  20.     if (NULL == lq.front)  
  21.     {  
  22.         printf("Error. malloc is fail.../n" );  
  23.         exit(1);  
  24.     }  
  25.     lq.rear->data=lq.front->data=-1;  
  26.     lq.rear->next=lq.front->next=NULL;  
  27.     return  lq;  
  28. }  
  29. int  empty_queue(linkqueue lq)  
  30. {  
  31.     if (lq.front == lq.rear)  
  32.         return  1;  
  33.      else   
  34.         return  0;  
  35. }  
  36. linkqueue insert_item(linkqueue lq, int  data)  
  37. {  
  38.     pnode pq;  
  39.     pq=(pnode)malloc(sizeof (node));  
  40.     if (pq == NULL)  
  41.     {  
  42.         printf("Error. malloc is fail.../n" );  
  43.         exit(1);  
  44.     }  
  45.     pq->data=data;  
  46.     pq->next=lq.rear->next;  
  47.     lq.rear->next=pq;  
  48.     lq.rear=lq.rear->next;  
  49.     return  lq;  
  50. }  
  51. linkqueue delete_item(linkqueue lq, int  *data)  
  52. {  
  53.     if (empty_queue(lq))  
  54.     {  
  55.         printf("queue is empty.../n" );  
  56.         exit(1);  
  57.     }  
  58.     *data=lq.front->data;  
  59.     lq.front=lq.front->next;  
  60.     return  lq;  
  61. }  
  62. int  len_queue(linkqueue lq)  
  63. {  
  64.     int  len=0;  
  65.     while (lq.front)  
  66.     {  
  67.         len++;  
  68.         lq.front=lq.front->next;  
  69.     }  
  70.     return  len;  
  71. }  
  72. void  display(linkqueue lq)  
  73. {  
  74.     linkqueue p;  
  75.     p=lq;  
  76.     if (empty_queue(lq))  
  77.     {  
  78.         printf("queue is empty.../n" );  
  79.         return ;  
  80.     }  
  81.     while (p.front->next)  
  82.     {  
  83.         printf("%4d" , p.front->data);  
  84.         p.front=p.front->next;  
  85.     }  
  86.     printf("%4d/n/n" , p.front->data);  
  87. }  
  88. void  main()  
  89. {  
  90.     int  *data = ( int  *)malloc( sizeof ( int ));  
  91.     linkqueue lq;  
  92.     lq=init_queue();  
  93.     lq=insert_item(lq, 1);  
  94.     lq=insert_item(lq, 2);  
  95.     lq=insert_item(lq, 3);  
  96.     lq=insert_item(lq, 4);  
  97.     lq=insert_item(lq, 5);  
  98.     display(lq);  
  99.     printf("len of queue is: %d/n/n" , len_queue(lq));  
  100.     lq=delete_item(lq, data);  
  101.     printf("delete %d/n" , *data);  
  102.     display(lq);  
  103.     lq=delete_item(lq, data);  
  104.     printf("delete %d/n" , *data);  
  105.     display(lq);  
  106.     getch();  
  107. }  

运行结果：


 

各种基本算法实现小结（三）—— 树与二叉树

（均已测试通过）

===================================================================

二叉树——先序

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <malloc.h>   
  3. #include <stdlib.h>   
  4. struct  _node  
  5. {  
  6.     char  data;  
  7.     struct  _node *lchild;  
  8.     struct  _node *rchild;  
  9. };  
  10. typedef   struct  _node node, *pnode;  
  11. pnode create_tree()  
  12. {  
  13.     pnode pt;  
  14.     char  data;  
  15.     scanf("%c" , &data);  
  16.     getchar();  
  17.     if (data== ' ' )  
  18.         pt=NULL;  
  19.     else   
  20.     {  
  21.         pt=(pnode)malloc(sizeof (node));  
  22.         pt->data=data;  
  23.         pt->lchild=create_tree();  
  24.         pt->rchild=create_tree();  
  25.     }  
  26.     return (pt);  
  27. }  
  28. void  print_pretree(pnode ps)  
  29. {  
  30.     if (ps != NULL)  
  31.     {  
  32.         printf("%3c" , ps->data);  
  33.         print_pretree(ps->lchild);  
  34.         print_pretree(ps->rchild);  
  35.     }     
  36. }  
  37. void  main()  
  38. {  
  39.     pnode ps;  
  40.     ps=create_tree();  
  41.     print_pretree(ps);  
  42.     printf("/n" );  
  43. }  

运行结果：

    

===========================================================

二叉树——各种操作

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <malloc.h>   
  3. struct  _node  
  4. {  
  5.     char  data;  
  6.     struct  _node *lchild;  
  7.     struct  _node *rchild;  
  8. };  
  9. typedef   struct  _node node, *pnode;  
  10. int  count_l=0;   /* count leaf */   
  11. int  count_n=0;   /* count node */   
  12. pnode create_tree()  
  13. {  
  14.     pnode pt;  
  15.     char  data;  
  16.     scanf("%c" , &data);  
  17.     getchar();  
  18.     if (data== ' ' )  
  19.         pt=NULL;  
  20.     else   
  21.     {  
  22.         pt=(pnode)malloc(sizeof (node));  
  23.         pt->data=data;  
  24.         pt->lchild=create_tree();  
  25.         pt->rchild=create_tree();  
  26.     }  
  27.     return (pt);  
  28. }  
  29. void  print_pretree(pnode ps)  
  30. {  
  31.     if (ps != NULL)  
  32.     {  
  33.         printf("%3c" , ps->data);  
  34.         print_pretree(ps->lchild);  
  35.         print_pretree(ps->rchild);  
  36.     }     
  37. }  
  38. void  print_midtree(pnode ps)  
  39. {  
  40.     if (ps != NULL)  
  41.     {  
  42.         print_midtree(ps->lchild);  
  43.       
  44.         printf("%3c" , ps->data);  
  45.         print_midtree(ps->rchild);     
  46.     }  
  47. }  
  48. void  print_posttree(pnode ps)  
  49. {  
  50.     if (ps != NULL)  
  51.     {  
  52.         print_posttree(ps->lchild);  
  53.         print_posttree(ps->rchild);  
  54.         printf("%3c" , ps->data);  
  55.     }  
  56. }  
  57. int  count_leaf(pnode ps)  
  58. {     
  59.     if (ps != NULL)  
  60.     {  
  61.         if (ps->lchild == NULL && ps->rchild == NULL)  
  62.         count_l++;    
  63.         count_leaf(ps->lchild);  
  64.         count_leaf(ps->rchild);  
  65.     }  
  66.     return  count_l;  
  67. }  
  68. int  count_node(pnode ps)  
  69. {  
  70.     if (ps != NULL)  
  71.     {  
  72.         count_n++;  
  73.         count_node(ps->lchild);  
  74.         count_node(ps->rchild);  
  75.     }  
  76.     return  count_n;  
  77. }  
  78. int  count_depth(pnode ps)  
  79. {  
  80.     int  ldep, rdep;  
  81.     if (ps == NULL)  
  82.         return  0;  
  83.     else   
  84.     {  
  85.         ldep=count_depth(ps->lchild);  
  86.         rdep=count_depth(ps->rchild);  
  87.           
  88.         return  ldep>rdep ? (ldep+1) : (rdep+1);  
  89.     }  
  90. }  
  91. void  main()  
  92. {  
  93.     pnode ps;  
  94.     ps=create_tree();  
  95.       
  96.     printf("pre order.../n" );  
  97.     print_pretree(ps);  
  98.     printf("/n" );  
  99.     printf("mid order.../n" );  
  100.     print_midtree(ps);  
  101.     printf("/n" );  
  102.     printf("post order.../n" );  
  103.     print_posttree(ps);  
  104.     printf("/n" );  
  105.     printf("number of leaf is: %d/n" , count_leaf(ps));  
  106.     printf("number of node is: %d/n" , count_node(ps));  
  107.     printf("max  of  depth is: %d/n" , count_depth(ps));  
  108. }  

运行结果：

     

===========================================================

二叉树——先序、中序、后序的递归与非递归实现

测试环境：VS2008 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include "stdafx.h"   
  2. #include <stdlib.h>   
  3. #include <malloc.h>   
  4. #define DataType char   
  5. /**************************************/   
  6. /********     树的结构定义     ********/   
  7. /**************************************/   
  8. struct  _tree  
  9. {  
  10.     DataType data;  
  11.     struct  _tree *lchild;  
  12.     struct  _tree *rchild;  
  13. };  
  14. typedef   struct  _tree tree, *ptree;  
  15. /**************************************/   
  16. /********     栈的结构定义     ********/   
  17. /**************************************/   
  18. struct  _node  
  19. {  
  20.     ptree pt;  
  21.     struct  _node *next;  
  22. };  
  23. typedef   struct  _node node, *pnode;  
  24. struct  _stack  
  25. {  
  26.     int  size;  
  27.     pnode ptop;  
  28. };  
  29. typedef   struct  _stack stack, *pstack;  
  30. /**************************************/   
  31. /********     堆的结构定义     ********/   
  32. /**************************************/   
  33. struct  _queue  
  34. {  
  35.     pnode front;  
  36.     pnode rear;  
  37. };  
  38. typedef   struct  _queue queue, *pqueue;  
  39. /**************************************/   
  40. /********     栈的数据操作     ********/   
  41. /**************************************/   
  42. pstack init_stack()  
  43. {  
  44.     pnode pn=NULL;  
  45.     pstack ps=NULL;  
  46.     pn=(pnode)malloc(sizeof (node));  
  47.     ps=(pstack)malloc(sizeof (stack));  
  48.     pn->pt=NULL;  
  49.     pn->next=NULL;  
  50.     ps->ptop=pn;  
  51.     return  ps;  
  52. }  
  53. int  empty_stack(pstack ps)  
  54. {  
  55.     if (ps->ptop->next==NULL)  
  56.         return  1;  
  57.     else   
  58.         return  0;  
  59. }  
  60. void  push_stack(pstack ps, ptree pt)  /* flag for post tree: 0 for lchild; 1 for rchild */   
  61. {  
  62.     pnode pn=NULL;  
  63.     pn=(pnode)malloc(sizeof (node));  
  64.     pn->pt=pt;  
  65.     pn->next=ps->ptop;  
  66.     ps->ptop=pn;  
  67. }  
  68. ptree pop_stack(pstack ps)  
  69. {  
  70.     ptree pt=NULL;  
  71.     pnode pn=NULL;  
  72.     if (!empty_stack(ps))  
  73.     {  
  74.         pn=ps->ptop;  
  75.         ps->ptop=ps->ptop->next;  
  76.         pt=pn->pt;  
  77.         free(pn);  
  78.     }  
  79.     return  pt;  
  80. }  
  81. ptree gettop_stack(pstack ps)  
  82. {  
  83.     if (!empty_stack(ps))  
  84.         return  ps->ptop->pt;  
  85. }  
  86. /**************************************/   
  87. /********     堆的数据操作     ********/   
  88. /**************************************/   
  89. queue init_queue()  
  90. {  
  91.     pnode pn=NULL;  
  92.     queue qu;  
  93.     pn=(pnode)malloc(sizeof (node));  
  94.     pn->pt=NULL;  
  95.     pn->next=NULL;  
  96.     qu.front=qu.rear=pn;  
  97.     return  qu;  
  98. }  
  99. int  empty_queue(queue qu)  
  100. {  
  101.     if (qu.front==qu.rear)  
  102.         return  1;  
  103.     else   
  104.         return  0;  
  105. }  
  106. void  en_queue(queue qu, ptree pt)  
  107. {  
  108.     pnode pn=NULL;  
  109.     pn=(pnode)malloc(sizeof (node));  
  110.     pn->pt;  
  111.     pn->next=qu.rear->next;  
  112.     qu.rear=pn;  
  113. }  
  114. ptree de_queue(queue qu)  
  115. {  
  116.     ptree pt=NULL;  
  117.     pnode pn=NULL;  
  118.     if (!empty_queue(qu))  
  119.     {  
  120.         pn=qu.front;  
  121.         qu.front=qu.front->next;  
  122.         pt=pn->pt;  
  123.         free(pn);  
  124.     }  
  125.     return  pt;  
  126. }  
  127. /**************************************/   
  128. /********     堆的数据操作     ********/   
  129. /**************************************/   
  130. ptree init_tree()  
  131. {  
  132.     ptree pt=NULL;  
  133.     pt=(ptree)malloc(sizeof (tree));  
  134.     pt->data='0' ;  
  135.     pt->lchild=NULL;  
  136.     pt->rchild=NULL;  
  137.     return  pt;  
  138. }  
  139. ptree create_tree()  
  140. {  
  141.     char  ch;  
  142.     ptree pt=NULL;  
  143.       
  144.     scanf("%c" , &ch);  
  145.     getchar();    
  146.     if (ch== ' ' )  
  147.         return  NULL;  
  148.     else   
  149.     {  
  150.         pt=(ptree)malloc(sizeof (tree));  
  151.         pt->data=ch;  
  152.         pt->lchild=create_tree();  
  153.         pt->rchild=create_tree();  
  154.     }  
  155.     return  pt;  
  156. }  
  157. void  print_pretree(ptree pt)  
  158. {  
  159.     if (pt!=NULL)  
  160.     {  
  161.         printf("%3c" , pt->data);  
  162.         print_pretree(pt->lchild);  
  163.         print_pretree(pt->rchild);  
  164.     }  
  165. }  
  166. void  print_pretree2(ptree pt)  
  167. {  
  168.     pstack ps=NULL;  
  169.     ptree p=NULL;  
  170.     ps=init_stack();  
  171.     p=pt;  
  172.     while (p!=NULL || !empty_stack(ps))  
  173.     {  
  174.         while (p!=NULL)  
  175.         {  
  176.             printf("%3c" , p->data);  
  177.             push_stack(ps, p);  
  178.             p=p->lchild;  
  179.         }  
  180.         if (!empty_stack(ps))  
  181.         {  
  182.             p=pop_stack(ps);  
  183.             p=p->rchild;  
  184.         }  
  185.     }  
  186. }  
  187. void  print_midtree(ptree pt)  
  188. {  
  189.     if (pt!=NULL)  
  190.     {  
  191.         print_midtree(pt->lchild);  
  192.         printf("%3c" , pt->data);  
  193.         print_midtree(pt->rchild);  
  194.     }  
  195. }  
  196. void  print_midtree2(ptree pt)  
  197. {  
  198.     pstack ps=NULL;  
  199.     ptree p=NULL;  
  200.     ps=init_stack();  
  201.     p=pt;  
  202.     while  (p!=NULL || !empty_stack(ps))  
  203.     {  
  204.         while (p!=NULL)  
  205.         {  
  206.             push_stack(ps, p);  
  207.             p=p->lchild;       
  208.         }  
  209.         if (!empty_stack(ps))  
  210.         {             
  211.             p=pop_stack(ps);  
  212.             printf("%3c" , p->data);  
  213.             p=p->rchild;  
  214.         }  
  215.     }  
  216. }  
  217. void  print_posttree(ptree pt)  
  218. {  
  219.     if (pt!=NULL)  
  220.     {  
  221.         print_posttree(pt->lchild);        
  222.         print_posttree(pt->rchild);    
  223.         printf("%3c" , pt->data);  
  224.     }  
  225. }  
  226. void  print_posttree2(ptree pt)  
  227. {  
  228.     pstack ps=NULL;  
  229.     ptree p=NULL;  
  230.     ptree p2=NULL;  
  231.     ptree lastvisit=NULL;  
  232.     ps=init_stack();  
  233.     p=pt;  
  234.     while  (p!=NULL || !empty_stack(ps))  
  235.     {  
  236.         while (p!=NULL)  
  237.         {  
  238.             push_stack(ps, p);  
  239.             p=p->lchild;                   
  240.         }  
  241.         p2=gettop_stack(ps); /* top: rchild==null or sub_root */   
  242.         if (p2->rchild==NULL || p2->rchild==lastvisit)  
  243.         {  
  244.             printf("%3c" , p2->data);  
  245.             lastvisit=pop_stack(ps); /* pop */   
  246.         }  
  247.         else   
  248.             p=p2->rchild;  
  249.     }     
  250. }  
  251. int  _tmain( int  argc, _TCHAR* argv[])  
  252. {  
  253.     ptree pt=NULL;  
  254.     /*pt=init_tree();*/   
  255.       
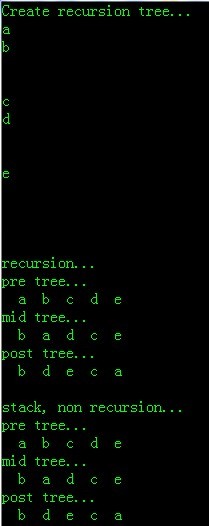
  256.     printf("Create recursion tree.../n" );  
  257.     pt=create_tree();  
  258.     /************  recursion ************/   
  259.     printf("/n/nrecursion..." );  
  260.     printf("/npre tree.../n" );  
  261.     print_pretree(pt);  
  262.     printf("/nmid tree.../n" );  
  263.     print_midtree(pt);  
  264.     printf("/npost tree.../n" );  
  265.     print_posttree(pt);  
  266.     /************  stack ************/   
  267.     printf("/n/nstack, non recursion..." );  
  268.     printf("/npre tree.../n" );  
  269.     print_pretree2(pt);  
  270.     printf("/nmid tree.../n" );  
  271.     print_midtree2(pt);  
  272.     printf("/npost tree.../n" );  
  273.     print_posttree2(pt);  
  274.     printf("/n" );  
  275.     return  0;  
  276. }  

运行结果：

      

===========================================================

二叉树——学习交流与修正改进

在网上看到了好多人转载这段代码，我也复制、粘贴下来学习

但在VC6.0编译器上运行并未通过，于是调试修正了几个小bug

测试运行通过后的代码粘贴如下，希望对大家学习有所帮助，谢谢！

本算法源码引用网址：http://www.ccrun.com/article.asp?i=292&d=y6y12h （二叉树实现源代码）


测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <conio.h>   
  2. #include <stdio.h>   
  3. #include <stdlib.h>   
  4. #define OK 1   
  5. #define ERROR 0   
  6. #define TRUE 1   
  7. #define FALSE 0   
  8. #define OVERFLOW -2   
  9. typedef   int  status;  
  10. typedef   struct  BiNode  
  11. {  
  12.     char  Data;  
  13.     struct  BiNode* lChild;  
  14.     struct  BiNode* rChild;  
  15. }BiNode,*pBiNode;  
  16. status CreateTree(BiNode** pTree);  
  17. status PreOrderTraval(BiNode* pTree);  
  18. status InOrderTraval(BiNode* pTree);  
  19. status PostOrderTraval(BiNode* pTree);  
  20. status Visit(char  Data);  
  21. status ShowLeaves(BiNode* pTree);  
  22. status DelTree(BiNode* pTree);  
  23. status Display(BiNode* pTree,int  Level);  
  24. status Clear(BiNode* pTree);  
  25. BiNode *pRoot=NULL;  
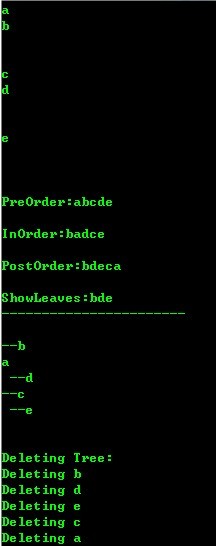
  26. void  main()  
  27. {  
  28.     CreateTree(&pRoot);  
  29.     printf("/nPreOrder:" );  
  30.     PreOrderTraval(pRoot);  
  31.     printf("/n" );  
  32.     printf("/nInOrder:" );  
  33.     InOrderTraval(pRoot);  
  34.     printf("/n" );  
  35.     printf("/nPostOrder:" );  
  36.     PostOrderTraval(pRoot);  
  37.     printf("/n" );  
  38.     printf("/nShowLeaves:" );  
  39.     ShowLeaves(pRoot);  
  40.     printf("/n-----------------------/n" );  
  41.     printf("/n" );  
  42.     Display(pRoot,0);  
  43.     printf("/n" );  
  44.     printf("/nDeleting Tree:/n" );  
  45.     DelTree(pRoot);  
  46.     printf("BiTree Deleted." );  
  47. }  
  48. status CreateTree(BiNode** pTree)   
  49. {  
  50.     char  ch;  
  51.     scanf("%c" ,&ch);  
  52.     getchar();  
  53.       
  54.     if (ch== ' ' )   /* NOTE: enter space, example: [ab  cd  e  ] */   
  55.     {  
  56.         (*pTree)=NULL;  
  57.     }  
  58.     else   
  59.     {  
  60.         if (!((*pTree)=(BiNode*)malloc( sizeof (BiNode))))  
  61.         {  
  62.             exit(OVERFLOW);  
  63.         }  
  64.         (*pTree)->Data=ch;  
  65.         CreateTree(&((*pTree)->lChild));  
  66.         CreateTree(&((*pTree)->rChild));  
  67.     }  
  68. return  OK;  
  69. }  
  70. status PreOrderTraval(BiNode* pTree)  
  71. {  
  72.     if (pTree)  
  73.     {  
  74.         if (Visit(pTree->Data))  
  75.         {  
  76.             if (PreOrderTraval(pTree->lChild))  
  77.             {  
  78.                 if (PreOrderTraval(pTree->rChild))  
  79.                 {  
  80.                     return  OK;  
  81.                 }  
  82.             }  
  83.         }  
  84.         return  ERROR;  
  85.     }  
  86.     else   
  87.     {  
  88.         return  OK;  
  89.     }  
  90. }  
  91. status InOrderTraval(BiNode* pTree)  
  92. {  
  93.     if (pTree)  
  94.     {  
  95.         if (InOrderTraval(pTree->lChild))  
  96.         {  
  97.             if (Visit(pTree->Data))  
  98.             {  
  99.                 if (InOrderTraval(pTree->rChild))  
  100.                 {  
  101.                     return  OK;  
  102.                 }  
  103.             }  
  104.             return  ERROR;  
  105.         }  
  106.         return  ERROR;  
  107.     }  
  108.     else   
  109.         return  OK;  
  110. }  
  111. status PostOrderTraval(BiNode* pTree)  
  112. {  
  113.     if (pTree)  
  114.     {  
  115.         if (PostOrderTraval(pTree->lChild))       
  116.         {  
  117.             if (PostOrderTraval(pTree->rChild))   
  118.             {  
  119.                 if (Visit(pTree->Data))  
  120.                 {  
  121.                     return  OK;  
  122.                 }  
  123.                 return  ERROR;  
  124.             }  
  125.         }  
  126.         return  ERROR;  
  127.     }  
  128.     else   
  129.     {  
  130.         return  OK;  
  131.     }  
  132. }  
  133. status Visit(char  Data)  
  134. {  
  135.     printf("%c" ,Data);  
  136.     return  OK;  
  137. }  
  138. status Display(BiNode* pTree,int  Level)  
  139. {  
  140.     int  i;  
  141.     if (pTree==NULL)   
  142.         return  FALSE;  
  143.     Display(pTree->lChild,Level+1);  
  144.     for (i=0;i<Level-1;i++)  
  145.     {  
  146.         printf(" " );  
  147.     }  
  148.     if (Level>=1)  
  149.     {  
  150.         printf("--" );  
  151.     }  
  152.     printf("%c/n" ,pTree->Data);  
  153.     Display(pTree->rChild,Level+1);  
  154.     return  TRUE;  
  155. }  
  156. status ShowLeaves(BiNode* pTree)  
  157. {  
  158.     if (pTree)  
  159.     {  
  160.         if (ShowLeaves(pTree->lChild))  
  161.         {  
  162.             if (ShowLeaves(pTree->rChild))  
  163.             {  
  164.                 if ((pTree->lChild==NULL)&&(pTree->rChild==NULL))  
  165.                 {  
  166.                     if (!Visit(pTree->Data))  
  167.                     {  
  168.                         return  ERROR;  
  169.                     }  
  170.                 }   
  171.                 return  OK;  
  172.             }  
  173.         }  
  174.         return  ERROR;  
  175.     }  
  176.     else   
  177.     {  
  178.         return  OK;  
  179.     }  
  180. }  
  181. status DelTree(BiNode* pTree)  
  182. {  
  183.     if (pTree)  
  184.     {  
  185.         if (DelTree(pTree->lChild))  
  186.         {  
  187.             if (DelTree(pTree->rChild))  
  188.             {  
  189.                 printf("Deleting %c/n" ,pTree->Data);  
  190.                 free((void *)pTree);  
  191.                 return  OK;  
  192.             }  
  193.         }  
  194.         return  ERROR;  
  195.     }  
  196.     else   
  197.         return  OK;  
  198. }   

运行结果：

    

===========================================================

上述代码改进后，逻辑更清晰 ，并添加了计算二叉树层次的函数 ShowDepth(BiNode* pTree)

具体代码如下：

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <conio.h>   
  2. #include <stdio.h>   
  3. #include <stdlib.h>   
  4. #define OK 1   
  5. #define ERROR 0   
  6. #define TRUE 1   
  7. #define FALSE 0   
  8. #define OVERFLOW -2   
  9. typedef   int  status;  
  10. typedef   struct  BiNode  
  11. {  
  12.     char  Data;  
  13.     struct  BiNode* lChild;  
  14.     struct  BiNode* rChild;  
  15. }BiNode,*pBiNode;  
  16. status CreateTree(BiNode** pTree);  
  17. status PreOrderTraval(BiNode* pTree);  
  18. status InOrderTraval(BiNode* pTree);  
  19. status PostOrderTraval(BiNode* pTree);  
  20. status Visit(char  Data);  
  21. status ShowLeaves(BiNode* pTree);  
  22. status ShowDepth(BiNode* pTree);  
  23. status DelTree(BiNode* pTree);  
  24. status Display(BiNode* pTree,int  Level);  
  25. status Clear(BiNode* pTree);  
  26. BiNode *pRoot=NULL;  
  27. void  main()  
  28. {  
  29.     CreateTree(&pRoot);  
  30.     printf("/nPreOrder:" );  
  31.     PreOrderTraval(pRoot);  
  32.     printf("/n" );  
  33.     printf("/nInOrder:" );  
  34.     InOrderTraval(pRoot);  
  35.     printf("/n" );  
  36.     printf("/nPostOrder:" );  
  37.     PostOrderTraval(pRoot);  
  38.     printf("/n" );  
  39.     printf("/nShowLeaves:" );  
  40.     ShowLeaves(pRoot);  
  41.     printf("/nShowDepth:%d/n" , ShowDepth(pRoot));  
  42.     printf("/n------------------/n" );  
  43.     printf("/n" );  
  44.     Display(pRoot,0);  
  45.     printf("/n" );  
  46.     printf("/nDeleting Tree:/n" );  
  47.     DelTree(pRoot);  
  48.     printf("BiTree Deleted." );  
  49. }  
  50. status CreateTree(BiNode** pTree)   
  51. {  
  52.     char  ch;  
  53.     scanf("%c" ,&ch);  
  54.     getchar();  
  55.       
  56.     if (ch== ' ' )   /* NOTE: enter space, example: [ab  cd  e  ] */   
  57.         (*pTree)=NULL;  
  58.     else   
  59.     {  
  60.         if (!((*pTree)=(BiNode*)malloc( sizeof (BiNode))))  
  61.             exit(OVERFLOW);  
  62.         (*pTree)->Data=ch;  
  63.         CreateTree(&((*pTree)->lChild));  
  64.         CreateTree(&((*pTree)->rChild));  
  65.     }  
  66.     return  OK;  
  67. }  
  68. status PreOrderTraval(BiNode* pTree)  
  69. {  
  70.     if (pTree)  
  71.     {  
  72.         Visit(pTree->Data);  
  73.         PreOrderTraval(pTree->lChild);  
  74.         PreOrderTraval(pTree->rChild);  
  75.     }  
  76.     return  OK;  
  77. }  
  78. status InOrderTraval(BiNode* pTree)  
  79. {  
  80.     if (pTree)  
  81.     {  
  82.         InOrderTraval(pTree->lChild);  
  83.         Visit(pTree->Data);  
  84.         InOrderTraval(pTree->rChild);  
  85.     }  
  86.       
  87.     return  OK;  
  88. }  
  89. status PostOrderTraval(BiNode* pTree)  
  90. {  
  91.     if (pTree)  
  92.     {  
  93.         PostOrderTraval(pTree->lChild);      
  94.         PostOrderTraval(pTree->rChild);     
  95.         Visit(pTree->Data);  
  96.     }  
  97.       
  98.     return  OK;  
  99. }  
  100. status Visit(char  Data)  
  101. {  
  102.     printf("%c" ,Data);  
  103.     return  OK;  
  104. }  
  105. status Display(BiNode* pTree,int  Level)  
  106. {  
  107.     int  i;  
  108.     if (pTree==NULL)   
  109.         return  FALSE;  
  110.     Display(pTree->lChild,Level+1);  
  111.     for (i=0;i<Level-1;i++)  
  112.     {  
  113.         printf(" " );  
  114.     }  
  115.     if (Level>=1)  
  116.     {  
  117.         printf("--" );  
  118.     }  
  119.     printf("%c/n" ,pTree->Data);  
  120.     Display(pTree->rChild,Level+1);  
  121.     return  TRUE;  
  122. }  
  123. status ShowLeaves(BiNode* pTree)  
  124. {  
  125.     if (pTree)  
  126.     {  
  127.         ShowLeaves(pTree->lChild);  
  128.         ShowLeaves(pTree->rChild);  
  129.         if ((pTree->lChild==NULL)&&(pTree->rChild==NULL))  
  130.             Visit(pTree->Data);  
  131.     }  
  132.       
  133.     return  OK;  
  134. }  
  135. status ShowDepth(BiNode* pTree)  
  136. {  
  137.     int  ldep=0, rdep=0;  
  138.       
  139.     if (!pTree)  
  140.         return  0;  
  141.     else   
  142.     {  
  143.         ldep=ShowDepth(pTree->lChild);  
  144.         rdep=ShowDepth(pTree->rChild);  
  145.         return  ldep>rdep ? (ldep+1) : (rdep+1);  
  146.     }  
  147. }  
  148. status DelTree(BiNode* pTree)  
  149. {  
  150.     if (pTree)  
  151.     {  
  152.         DelTree(pTree->lChild);  
  153.         DelTree(pTree->rChild);  
  154.         printf("Deleting %c/n" ,pTree->Data);  
  155.         free((void *)pTree);  
  156.     }  
  157.     return  OK;  
  158. }   

运行结果：

      

===========================================================

 

各种基本算法实现小结（四）—— 图及其遍历

（均已测试通过）

====================================================================

图——深度优先和广度优先算法

无向图用二维邻接矩阵表示

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <malloc.h>   
  3. #include <stdlib.h>   
  4. #define INFINITY 32767   
  5. #define MAX_VEX 20   
  6. #define QUEUE_SIZE (MAX_VERTEX+1)   
  7. #define DataType char  /* vertext's info  */   
  8. int  *visited;  /* Node: visited flag with dynamic array, good idea ! */   
  9. /* init queue for bfs */   
  10. struct  _node  
  11. {  
  12.     int  v_num;  
  13.     struct  _node *next;  
  14. };  
  15. typedef   struct  _node node, *pnode;  
  16. struct  _queue  
  17. {  
  18.     pnode front;  
  19.     pnode rear;  
  20. };  
  21. typedef   struct  _queue queue, *pqueue;  
  22. struct  _graph  
  23. {  
  24.     DataType *vexs;  
  25.     int  arcs[MAX_VEX][MAX_VEX];  
  26.     int  vexnum, arcnum;  
  27. };  
  28. typedef   struct  _graph graph, *pgraph;  
  29. /* operation of queue */   
  30. queue init_queue()  
  31. {  
  32.     queue qu;  
  33.     qu.front=qu.rear=(pnode)malloc(sizeof (node));  
  34.     if (qu.front == NULL)  
  35.         exit(1);  
  36.     qu.rear->next=NULL;  
  37.     return  qu;  
  38. }  
  39. void  en_queue(pqueue pqu,  int  v_num)  
  40. {  
  41.     pnode pn;  
  42.     pn=(pnode)malloc(sizeof (node));  
  43.     if (pqu->front == NULL)  
  44.         exit(1);  
  45.     pn->v_num=v_num;  
  46.     pn->next=NULL;  
  47.     pqu->rear->next=pn;  
  48.     pqu->rear=pqu->rear->next;  
  49. }  
  50. int  isempty_queue(pqueue pqu)  
  51. {  
  52.     if (pqu->front == pqu->rear)  
  53.         return  1;  
  54.     else   
  55.         return  0;  
  56. }  
  57. int  de_queue(pqueue pqu)  
  58. {  
  59.     pnode pn;  
  60.     int  d;  
  61.     if (isempty_queue(pqu))  
  62.         return  -1;  
  63.     pn=pqu->front;  
  64.     d=pn->v_num;  
  65.     pqu->front=pn->next;  
  66.     free(pn);  
  67.     return  d;  
  68. }  
  69. int  locate(graph g, DataType data)  
  70. {  
  71.     int  i;  
  72.     for (i=0;i<g.vexnum;i++)  
  73.         if (g.vexs[i] == data)  
  74.             return  i;  
  75.      return  -1;  
  76. }  
  77. graph create_graph()  
  78. {  
  79.     int  i,j,w, s1,s2;  
  80.     DataType ch1,ch2,tmp;  
  81.     graph g;  
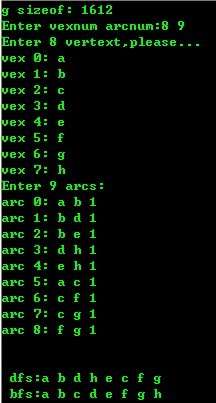
  82.     printf("g sizeof: %d/n" ,  sizeof (g));  
  83.     printf("Enter vexnum arcnum:" );  
  84.     scanf("%d %d" , &g.vexnum, &g.arcnum);  
  85.     tmp=getchar();  
  86.     g.vexs=(DataType *)malloc(sizeof (DataType));  
  87.     if (g.vexs == NULL)  
  88.         exit(1);  
  89.     printf("Enter %d vertext,please.../n" , g.vexnum);  
  90.     for (i=0;i<g.vexnum;i++)  
  91.     {  
  92.         printf("vex %d: " , i);  
  93.         scanf("%c" , &g.vexs[i]);  
  94.         tmp=getchar();  
  95.         //visited[i]=0;   
  96.     }  
  97.     for (i=0;i<g.vexnum;i++)  
  98.         for (j=0;j<g.vexnum;j++)  
  99.             g.arcs[i][j]=INFINITY;  
  100.      printf("Enter %d arcs:/n" , g.arcnum);  
  101.      for (i=0;i<g.arcnum;i++)  
  102.      {  
  103.         printf("arc %d: " , i);  
  104.         scanf("%c %c %d" , &ch1, &ch2, &w);  
  105.         tmp=getchar();  
  106.         s1=locate(g, ch1);  
  107.         s2=locate(g, ch2);  
  108.         g.arcs[s1][s2]=g.arcs[s2][s1]=w; /* NOTE: weight */   
  109.      }  
  110.      return  g;  
  111. }  
  112. int  firstvex_graph(graph g,  int  k)  
  113. {  
  114.     int  i;  
  115.     if (k>=0 && k<g.vexnum)  
  116.         for (i=0;i<g.vexnum;i++)  
  117.             if (g.arcs[k][i] != INFINITY)  
  118.                 return  i;  
  119.      return  -1;  
  120. }  
  121. int  nextvex_graph(graph g,  int  i,  int  j)  
  122. {  
  123.     int  k;  
  124.     if (i>=0 && i<g.vexnum && j>=0 && j<g.vexnum)  
  125.         for (k=j+1; k<g.vexnum; k++)  
  126.             if (g.arcs[i][k] != INFINITY)  
  127.                 return  k;  
  128.      return  -1;  
  129. }  
  130. void  dfs(graph g,  int  k)  
  131. {  
  132.     int  i;  
  133.     if (k == -1)  
  134.     {  
  135.         for (i=0;i<g.vexnum;i++)  
  136.             if (!visited[i])  
  137.                 dfs(g,i);  
  138.      }  
  139.      else   
  140.      {  
  141.         visited[k]=1;  
  142.         printf("%c " , g.vexs[k]);  
  143.         for (i=firstvex_graph(g,k);i>=0;i=nextvex_graph(g,k,i))  
  144.             if (!visited[i])  
  145.                 dfs(g,i);  
  146.      }  
  147. }  
  148. void  bfs(graph g)  
  149. {  
  150.     int  i,j,k;  
  151.     queue qu;  
  152.     qu=init_queue();  
  153.     for (i=0;i<g.vexnum;i++)  
  154.         if (!visited[i])  
  155.         {  
  156.             visited[i] =1;  
  157.             printf("%c " , g.vexs[i]);  
  158.             en_queue(&qu, i);  
  159.             while (!isempty_queue(&qu))  
  160.             {  
  161.                 k=de_queue(&qu);  
  162.                 for (j=firstvex_graph(g,k); j>=0;j=nextvex_graph(g,k,j))  
  163.                     if (!visited[j])  
  164.                     {  
  165.                         visited[j]=1;  
  166.                         printf("%c " , g.vexs[j]);  
  167.                         en_queue(&qu, j);  
  168.                     }  
  169.             }  
  170.         }  
  171. }  
  172. void  main()  
  173. {  
  174.     int  i;  
  175.     graph g;  
  176.     g=create_graph();  
  177.     visited=(int  *)malloc(g.vexnum* sizeof ( int ));  
  178.     for (i=0;i<g.vexnum;i++)  
  179.         visited[i]=0;  
  180.     printf("/n/n dfs:" );  
  181.     dfs(g,-1);  
  182.     for (i=0;i<g.vexnum;i++)  
  183.         visited[i]=0;  
  184.     printf("/n bfs:" );  
  185.     bfs(g);  
  186.       
  187.     if (visited)  
  188.         free(visited);  
  189.     printf("/n" );  
  190. }  

运行结果：

     

======================================================

图 ——深度优先

测试环境：VS2008 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include "stdafx.h"   
  2. #include <stdlib.h>   
  3. #include <malloc.h>   
  4. #define MAX_VEX 20   
  5. #define INFINITY 65535   
  6. int  *visited;  
  7. struct  _node  
  8. {  
  9.     int  vex_num;  
  10.     struct  _node *next;  
  11. };  
  12. typedef   struct  _node node, *pnode;  
  13. struct  _graph  
  14. {  
  15.     char  *vexs;  
  16.     int  arcs[MAX_VEX][MAX_VEX];  
  17.     int  vexnum, arcnum;  
  18. };  
  19. typedef   struct  _graph graph, *pgraph;  
  20. int  locate(graph g,  char  ch)  
  21. {  
  22.     int  i;  
  23.     for (i=1; i<=g.vexnum; i++)  
  24.         if (g.vexs[i]==ch)  
  25.             return  i;  
  26.     return  -1;  
  27. }  
  28. graph create_graph()  
  29. {  
  30.     int  i, j, w, p1, p2;  
  31.     char  ch1, ch2;  
  32.     graph g;  
  33.     printf("Enter vexnum arcnum: " );  
  34.     scanf("%d %d" , &g.vexnum, &g.arcnum);  
  35.     getchar();  
  36.     for (i=1; i<=g.vexnum; i++)  
  37.         for (j=1; j<g.vexnum; j++)  
  38.             g.arcs[i][j]=INFINITY;  
  39.     g.vexs=(char  *)malloc( sizeof ( char ));  
  40.     printf("Enter %d vexnum.../n" , g.vexnum);  
  41.     for (i=1; i<=g.vexnum; i++)  
  42.     {  
  43.         printf("vex %d: " , i);  
  44.         scanf("%c" , &g.vexs[i]);  
  45.         getchar();  
  46.     }  
  47.     printf("Enter %d arcnum.../n" , g.arcnum);  
  48.     for (i=1; i<=g.arcnum; i++)  
  49.     {  
  50.         printf("arc %d: " , i);  
  51.         scanf("%c %c %d" , &ch1, &ch2, &w);  
  52.         getchar();  
  53.         p1=locate(g, ch1);  
  54.         p2=locate(g, ch2);  
  55.         g.arcs[p1][p2]=g.arcs[p2][p1]=w;  
  56.     }  
  57.     return  g;  
  58. }  
  59. int  firstvex_graph(graph g,  int  i)  
  60. {  
  61.     int  k;  
  62.     if (i>=1 && i<=g.vexnum)  
  63.         for (k=1; k<=g.vexnum; k++)  
  64.             if (g.arcs[i][k]!=INFINITY)  
  65.                 return  k;  
  66.     return  -1;  
  67. }  
  68. int  nextvex_graph(graph g,  int  i,  int  j)  
  69. {  
  70.     int  k;  
  71.     if (i>=1 && i<=g.vexnum && j>=1 && j<=g.vexnum)  
  72.         for (k=j+1; k<=g.vexnum; k++)  
  73.             if (g.arcs[i][k]!=INFINITY)  
  74.                 return  k;  
  75.     return  -1;  
  76. }  
  77. void  dfs(graph g,  int  i)  
  78. {  
  79.     int  k, j;  
  80.     if (!visited[i])  
  81.     {  
  82.         visited[i]=1;  
  83.         printf("%c" , g.vexs[i]);  
  84.         for (j=firstvex_graph(g, i); j>=1; j=nextvex_graph(g, i, j))  
  85.             if (!visited[j])  
  86.                 dfs(g, j);  
  87.     }  
  88. }  
  89. void  dfs_graph(graph g)  
  90. {  
  91.     int  i;  
  92.     visited=(int  *)malloc((g.vexnum+1)* sizeof ( int ));  
  93.     for (i=1; i<=g.vexnum; i++)  
  94.         visited[i]=0;  
  95.     for (i=1; i<g.vexnum; i++)  
  96.         if (!visited[i])  
  97.             dfs(g, i);  
  98. }  
  99. int  _tmain( int  argc, _TCHAR* argv[])  
  100. {  
  101.     graph g;  
  102.     g=create_graph();  
  103.     dfs_graph(g);  
  104.     printf("/n" );  
  105.     return  0;  
  106. }  

======================================================

图 ——广度优先

测试环境：VS2008 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include "stdafx.h"   
  2. #include <stdlib.h>   
  3. #include <malloc.h>   
  4. #define MAX_VEX 20   
  5. #define INFINITY 65535   
  6. int  *visited;  
  7. struct  _node  
  8. {  
  9.     int  data;  
  10.     struct  _node *next;  
  11. };  
  12. typedef   struct  _node node, *pnode;  
  13. struct  _queue  
  14. {  
  15.     pnode front;  
  16.     pnode rear;  
  17. };  
  18. typedef   struct  _queue queue, *pqueue;  
  19. queue init_queue()  
  20. {  
  21.     pnode pn=NULL;  
  22.     queue qu;  
  23.     pn=(pnode)malloc(sizeof (node));  
  24.     if (pn==NULL)  
  25.         printf("init queue, malloc is fail.../n" );  
  26.     pn->data=-1;  
  27.     pn->next=NULL;  
  28.     qu.front=qu.rear=pn;  
  29.     return  qu;  
  30. }  
  31. int  empty_queue(queue qu)  
  32. {  
  33.     if (qu.rear==qu.front)  
  34.         return  0;  
  35.     else   
  36.         return  1;  
  37. }  
  38. void  en_queue(pqueue pqu,  int  data)  
  39. {  
  40.     pnode pn=NULL;  
  41.     if (pqu->rear==NULL)  
  42.         return ;  
  43.     pn=(pnode)malloc(sizeof (node));  
  44.     pn->data=data;  
  45.     pn->next=pqu->rear->next;  
  46.     pqu->rear->next=pn;  
  47.     pqu->rear=pn;  
  48. }  
  49. int  de_queue(pqueue pqu)  
  50. {  
  51.     int  data;  
  52.     pnode pn=NULL;  
  53.     if (pqu->front->next==NULL)  
  54.         return  -1;  
  55.       
  56.     pn=pqu->front->next;  
  57.     pqu->front=pqu->front->next;  
  58.     data=pn->data;  
  59.     free(pn);  
  60.     return  data;  
  61. }  
  62. struct  _graph  
  63. {  
  64.     char  *vexs;  
  65.     int  arcs[MAX_VEX][MAX_VEX];  
  66.     int  vexnum, arcnum;  
  67. };  
  68. typedef  _graph graph, *pgraph;  
  69. int  locate(graph g,  char  ch)  
  70. {  
  71.     int  i;  
  72.     for (i=1; i<=g.vexnum; i++)  
  73.         if (g.vexs[i]==ch)  
  74.             return  i;  
  75.     return  -1;  
  76. }  
  77. graph create_graph()  
  78. {  
  79.     int  i, j, w, p1, p2;  
  80.     char  ch1, ch2;  
  81.     graph g;  
  82.     printf("Enter vexnum arcnum: " );  
  83.     scanf("%d %d" , &g.vexnum, &g.arcnum);  
  84.     getchar();  
  85.     for (i=1; i<=g.vexnum; i++)  
  86.         for (j=1; j<g.vexnum; j++)  
  87.             g.arcs[i][j]=INFINITY;  
  88.     g.vexs=(char  *)malloc((g.vexnum+1)* sizeof ( char ));  
  89.     printf("Enter %d vexnum.../n" , g.vexnum);  
  90.     for (i=1; i<=g.vexnum; i++)  
  91.     {  
  92.         printf("vex %d: " , i);  
  93.         scanf("%c" , &g.vexs[i]);  
  94.         getchar();  
  95.     }  
  96.     printf("Enter %d arcnum.../n" , g.arcnum);  
  97.     for (i=1; i<=g.arcnum; i++)  
  98.     {  
  99.         printf("arc %d: " , i);  
  100.         scanf("%c %c %d" , &ch1, &ch2, &w);  
  101.         getchar();  
  102.         p1=locate(g, ch1);  
  103.         p2=locate(g, ch2);  
  104.         g.arcs[p1][p2]=g.arcs[p2][p1]=w;  
  105.     }  
  106.     return  g;  
  107. }  
  108. int  firstvex_graph(graph g,  int  i)  
  109. {  
  110.     int  k;  
  111.     if (i>=1 && i<=g.vexnum)  
  112.         for (k=1; k<=g.vexnum; k++)  
  113.             if (g.arcs[i][k]!=INFINITY)  
  114.                 return  k;  
  115.     return  -1;  
  116. }  
  117. int  nextvex_graph(graph g,  int  i,  int  j)  
  118. {  
  119.     int  k;  
  120.     if (i>=1 && i<=g.vexnum && j>=1 && j<=g.vexnum)  
  121.         for (k=j+1; k<=g.vexnum; k++)  
  122.             if (g.arcs[i][k]!=INFINITY)  
  123.                 return  k;  
  124.     return  -1;  
  125. }  
  126. void  bfs(graph g)  
  127. {  
  128.     int  i, ivex, inextvex;  
  129.     visited=(int  *)malloc((g.vexnum+1)* sizeof ( int ));  
  130.     for (i=1; i<=g.vexnum; i++)  
  131.         visited[i]=0;  
  132.     queue qu=init_queue();  
  133.     for (i=1; i<=g.vexnum; i++)  
  134.     {  
  135.         if (!visited[i])  
  136.         {  
  137.             visited[i]=1;  
  138.             printf("%c" , g.vexs[i]);  
  139.             en_queue(&qu, i);  
  140.         }  
  141.           
  142.         while (!empty_queue(qu))  
  143.         {  
  144.             ivex=de_queue(&qu);  
  145.             for (inextvex=firstvex_graph(g, ivex); inextvex>=1; inextvex=nextvex_graph(g, ivex, inextvex))  
  146.                 if (!visited[inextvex])  
  147.                 {  
  148.                     visited[inextvex]=1;  
  149.                     printf("%c" , g.vexs[inextvex]);  
  150.                     en_queue(&qu, inextvex);  
  151.                 }  
  152.         }  
  153.     }  
  154. }  
  155. int  _tmain( int  argc, _TCHAR* argv[])  
  156. {  
  157.     graph g;  
  158.     g=create_graph();  
  159.     bfs(g);  
  160.     printf("/n" );  
  161.     return  0;  
  162. }  

======================================================

图 ——深度优先和广度优先算法2（网摘）

本文引用网址：http://bbs.bccn.net/thread-155311-1-1.html（编程论坛）

看到本算法在网上转载较多，比较流行，且能直接运行

但发现大多转载中，也把DFS与BFS正好写反了，对此本文已修正

此外，本算法混用了C与C++，不够单纯，申请的指针空间也未及时释放

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <malloc.h>   
  3. #define INFINITY 32767   
  4. #define MAX_VEX 20    
  5. #define QUEUE_SIZE (MAX_VEX+1)    
  6. bool  *visited;    
  7. typedef   struct   
  8. {  
  9.     char  *vexs;                     //顶点向量   
  10.     int  arcs[MAX_VEX][MAX_VEX];     //邻接矩阵   
  11.     int  vexnum,arcnum;              //图的当前顶点数和弧数   
  12. }Graph;  
  13. //队列类   
  14. class  Queue  
  15. {  
  16.     public :  
  17.     void  InitQueue(){  
  18.     base=(int  *)malloc(QUEUE_SIZE* sizeof ( int ));  
  19.     front=rear=0;  
  20. }  
  21. void  EnQueue( int  e)  
  22. {  
  23.     base[rear]=e;  
  24.     rear=(rear+1)%QUEUE_SIZE;  
  25. }  
  26. void  DeQueue( int  &e)  
  27. {  
  28.     e=base[front];  
  29.     front=(front+1)%QUEUE_SIZE;  
  30. }  
  31. public :  
  32.     int  *base;  
  33.     int  front;  
  34.     int  rear;  
  35. };  
  36. //图G中查找元素c的位置   
  37. int  Locate(Graph G, char  c)  
  38. {  
  39.     for ( int  i=0;i<G.vexnum;i++)  
  40.         if (G.vexs[i]==c)   
  41.             return  i;  
  42.       
  43.     return  -1;  
  44. }  
  45. //创建无向网   
  46. void  CreateUDN(Graph &G){  
  47.     int  i,j,w,s1,s2;  
  48.     char  a,b,temp;  
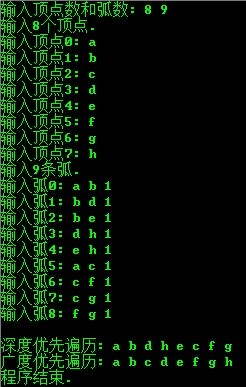
  49.     printf("输入顶点数和弧数: " );  
  50.     scanf("%d%d" ,&G.vexnum,&G.arcnum);  
  51.     temp=getchar(); //接收回车   
  52.     G.vexs=(char  *)malloc(G.vexnum* sizeof ( char ));  //分配顶点数目   
  53.     printf("输入%d个顶点./n" ,G.vexnum);  
  54.     for (i=0;i<G.vexnum;i++)  //初始化顶点   
  55.     {   
  56.         printf("输入顶点%d: " ,i);  
  57.         scanf("%c" ,&G.vexs[i]);  
  58.         temp=getchar(); //接收回车    
  59.     }  
  60.     for (i=0;i<G.vexnum;i++)  //初始化邻接矩阵   
  61.         for (j=0;j<G.vexnum;j++)  
  62.             G.arcs[i][j]=INFINITY;  
  63.     printf("输入%d条弧./n" ,G.arcnum);  
  64.     for (i=0;i<G.arcnum;i++)  
  65.     { //初始化弧   
  66.         printf("输入弧%d: " ,i);  
  67.         scanf("%c %c %d" ,&a,&b,&w);  //输入一条边依附的顶点和权值   
  68.         temp=getchar(); //接收回车   
  69.         s1=Locate(G,a);  
  70.         s2=Locate(G,b);  
  71.         G.arcs[s1][s2]=G.arcs[s2][s1]=w;  
  72.     }  
  73. }  
  74. //图G中顶点k的第一个邻接顶点   
  75. int  FirstVex(Graph G, int  k)  
  76. {  
  77.     if (k>=0 && k<G.vexnum)  //k合理   
  78.         for ( int  i=0;i<G.vexnum;i++)  
  79.             if (G.arcs[k][i]!=INFINITY)  return  i;  
  80.   return  -1;  
  81. }  
  82. //图G中顶点i的第j个邻接顶点的下一个邻接顶点   
  83. int  NextVex(Graph G, int  i, int  j)  
  84. {  
  85.     if (i>=0 && i<G.vexnum && j>=0 && j<G.vexnum)  //i,j合理   
  86.         for ( int  k=j+1;k<G.vexnum;k++)  
  87.             if (G.arcs[i][k]!=INFINITY)   
  88.                 return  k;  
  89.   return  -1;  
  90. }  
  91. //深度优先遍历   
  92. void  DFS(Graph G, int  k)  
  93. {  
  94.     int  i;  
  95.     if (k==-1)  //第一次执行DFS时,k为-1   
  96.     {  
  97.         for (i=0;i<G.vexnum;i++)  
  98.             if (!visited[i])   
  99.                 DFS(G,i); //对尚未访问的顶点调用DFS   
  100.     }  
  101.     else   
  102.     {   
  103.         visited[k]=true ;  
  104.         printf("%c " ,G.vexs[k]);  //访问第k个顶点   
  105.         for (i=FirstVex(G,k);i>=0;i=NextVex(G,k,i))  
  106.             if (!visited[i])  //对k的尚未访问的邻接顶点i递归调用DFS   
  107.                 DFS(G,i);   
  108.     }  
  109. }  
  110. //广度优先遍历   
  111. void  BFS(Graph G)  
  112. {  
  113.     int  k;  
  114.     Queue Q; //辅助队列Q   
  115.     Q.InitQueue();  
  116.     for ( int  i=0;i<G.vexnum;i++)  
  117.         if (!visited[i])  //i尚未访问   
  118.         {   
  119.             visited[i]=true ;  
  120.             printf("%c " ,G.vexs[i]);  
  121.              Q.EnQueue(i); //i入列   
  122.             while (Q.front!=Q.rear)  
  123.             {  
  124.                 Q.DeQueue(k); //队头元素出列并置为k   
  125.                 for ( int  w=FirstVex(G,k);w>=0;w=NextVex(G,k,w))  
  126.                     if (!visited[w])  //w为k的尚未访问的邻接顶点   
  127.                     {   
  128.                         visited[w]=true ;  
  129.                         printf("%c " ,G.vexs[w]);  
  130.                         Q.EnQueue(w);  
  131.                     }  
  132.             }  
  133.         }  
  134. }  
  135. //主函数   
  136. void  main(){  
  137.     int  i;  
  138.     Graph G;  
  139.     CreateUDN(G);  
  140.     visited=(bool  *)malloc(G.vexnum* sizeof ( bool ));   
  141.     printf("/n深度优先遍历: " );   
  142.     for (i=0;i<G.vexnum;i++)  
  143.         visited[i]=false ;  
  144.     DFS(G,-1); /* NODE: DFS */   
  145.     printf("/n广度优先遍历: " );   
  146.     for (i=0;i<G.vexnum;i++)  
  147.         visited[i]=false ;  
  148.     BFS(G); /* NODE: BFS */   
  149.     printf("/n程序结束./n" );  
  150. }  

运行结果：

    

======================================================

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
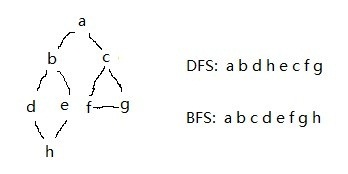
  1. #include <iostream.h>    
  2. #include <stdlib.h>    
  3. #define INFINITY 0    
  4. #define MAX_VERTEX_NUM 10 //最大顶点数    
  5. #define MAX_EDGE_NUM 40 //最大边数    
  6. typedef   enum  {DG,DN,UDG,UDN}Graphkind;   
  7. typedef   char  VertexType;  //顶点数据类型    
  8. typedef   struct  ArcCell   
  9. {   
  10. int  adj;  //无权图，1或0表示相邻否；带权图则是权值。    
  11. //int *info;    
  12. }ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];   
  13. typedef   struct    
  14. {   
  15. VertexType vexs[MAX_VERTEX_NUM]; //顶点向量    
  16. AdjMatrix arcs; //邻接矩阵    
  17. int  vexnum,arcnum;  //图的当前顶点数和弧数。    
  18. Graphkind kind;   
  19. }MGraph;   
  20. int  LocateVex(MGraph G,VertexType v1)   
  21. {   
  22. int  i;   
  23. for (i=0;i<G.vexnum;i++)   
  24. if (G.vexs[i]==v1)   
  25. return  i;   
  26. return  -1;   
  27. }   
  28. int  CreatUDN(MGraph &G)   
  29. // 采用数组表示法，构造无向网 G    
  30. {   
  31. VertexType v1,v2;   
  32. int  w,j;   
  33. cout<<"输入图的顶点数" <<endl;   
  34. cin>>G.vexnum;   
  35. cout<<"输入图的弧数" <<endl;   
  36. cin>>G.arcnum;   
  37. for ( int  i=0;i<G.vexnum;i++)   
  38. {   
  39. cout<<"输入顶点向量" <<endl;   
  40. cin>>G.vexs[i];   
  41. }   
  42. for (i=0;i<G.vexnum;i++)   
  43. for (j=0;j<G.vexnum;j++)   
  44. {   
  45. G.arcs[i][j].adj=INFINITY;   
  46. }   
  47. for ( int  k=0;k<G.arcnum;++k)  //构造邻接矩阵    
  48. {   
  49. cout<<"输入边依附的两个顶点" <<endl;   
  50. cin>>v1>>v2;   
  51. cout<<"输入此边的权值" <<endl;   
  52. cin>>w;   
  53. i=LocateVex(G,v1);   
  54. j=LocateVex(G,v2);   
  55. G.arcs[i][j].adj=w;   
  56. G.arcs[j][i].adj=G.arcs[i][j].adj;   
  57. }   
  58. return  1;   
  59. }   
  60. void  dispMGraph(MGraph G)   
  61. {   
  62. cout<<"图的邻接矩阵图是：" <<endl;   
  63. for ( int  i=0;i<G.vexnum;i++)   
  64. {   
  65. for ( int  j=0;j<G.vexnum;j++)   
  66. cout<<" " <<G.arcs[i][j].adj;   
  67. cout<<endl;   
  68. }   
  69. }   
  70. void  main()   
  71. {   
  72. MGraph G;   
  73. CreatUDN(G);   
  74. dispMGraph(G);   
  75. }   
  76. // 邻接表 表示:    
  77. #include <iostream.h>    
  78. #include <stdlib.h>    
  79. #define MAX_VERTEX_NUM 20 //最大顶点数    
  80. #define MAX_EDGE_NUM 40 //最大边数    
  81. int  visited[ MAX_VERTEX_NUM];   
  82. typedef   int  VertexType ;  //顶点数据类型    
  83. typedef   struct  ArcNode   
  84. {   
  85. int  adjvex;   
  86. int  weight;   
  87. struct  ArcNode *nextarc;   
  88. }ArcNode;   
  89. typedef   struct  VNode   
  90. {   
  91. VertexType data;   
  92. ArcNode *firstarc;   
  93. }VNode,AdjList[MAX_VERTEX_NUM];   
  94. typedef   struct    
  95. {   
  96. AdjList vertices;   
  97. int  vexnum,arcnum;   
  98. int  kind;   
  99. }ALGraph;   
  100. void  CreateDG(ALGraph &G)   
  101. {   
  102. int  i,j,k;   
  103. ArcNode *p;   
  104. cout<<"创建一个图:" <<endl;   
  105. cout<<"顶点数:" ; cin>>G.vexnum;cout<<endl;   
  106. cout<<"边数:" ; cin>>G.arcnum; cout<<endl;   
  107. for (i=0;i<G.vexnum;i++)   
  108. {   
  109. G.vertices[i].data=i;   
  110. G.vertices[i].firstarc=NULL;   
  111. }   
  112. for (k=0;k<G.arcnum;k++)   
  113. {   
  114. cout<<"请输入第" <<k+1<< "条边:" ;   
  115. cin>>i>>j;   
  116. p=(ArcNode*)malloc(sizeof (ArcNode));   
  117. p->adjvex=j;   
  118. p->nextarc=G.vertices[i].firstarc;   
  119. G.vertices[i].firstarc=p;   
  120. }   
  121. }   
  122. void  Disp(ALGraph G)   
  123. {   
  124. int  i,j;   
  125. ArcNode *p;   
  126. cout<<"输出图为:" <<endl;   
  127. for (i=0;i<G.vexnum;i++)   
  128. {   
  129. p=G.vertices[i].firstarc;   
  130. j=0;   
  131. while (p!=NULL)   
  132. {   
  133. cout<<"(" <<i<< "," <<p->adjvex<< ")" ;   
  134. p=p->nextarc;   
  135. j=1;   
  136. }   
  137. if (j==1)   
  138. cout<<endl;   
  139. }   
  140. }   
  141. void  dfs(ALGraph G, int  v)  //深度优先遍历    
  142. {   
  143. ArcNode *p;   
  144. cout<<v<<" " ;   
  145. visited[v]=1;   
  146. p=G.vertices[v].firstarc;   
  147. while (p!=NULL)   
  148. { if (!visited[p->adjvex])   
  149. dfs(G,p->adjvex);   
  150. p=p->nextarc;   
  151. }   
  152. return  ;   
  153. }   
  154. void  dfs1(ALGraph G)   
  155. {   
  156. int  i;   
  157. for (i=0;i<G.vexnum;i++)   
  158. if (visited[i]==0)   
  159. dfs(G,i);   
  160. }   
  161. void  main()   
  162. {   
  163. ALGraph G;   
  164. CreateDG(G);   
  165. int  v;   
  166. Disp(G);   
  167. cout<<"输入顶点:" ;   
  168. cin>>v;   
  169. cout<<"深度优先序列:" ;   
  170. dfs1(G);   
  171. cout<<endl;   
  172. }  

各种基本算法实现小结（五）—— 排序算法

（均已测试通过）

* 选择排序 |____简单选择排序 |____堆排序 |____归并排序

* 交换排序 |____冒泡排序 |____快速排序

* 插入排序 |____直接插入排序 |____折半排序 |____希尔排序

* 分配排序 |____箱排序 |____基数排序

======================================================================

简单排序算法

1、 冒泡排序

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include   
  2.  <stdio.h>  
  3. #include <stdlib.h>   
  4. #include <time.h>   
  5. #define MAX 11   
  6. void  input( int  num[])  
  7. {  
  8.     int  i;  
  9.       
  10.     srand((unsigned)time(NULL));  
  11.     for (i=1; i<MAX; i++)  
  12.         num[i]=rand()%100;        
  13. }  
  14. void  output( int  num[])  
  15. {  
  16.     int  i;  
  17.       
  18.     for (i=1; i<MAX; i++)  
  19.     {  
  20.         printf("%5d" , num[i]);  
  21.         if (0 == i%10)  
  22.             printf("/n" );  
  23.     }  
  24.     printf("/n" );  
  25. }  
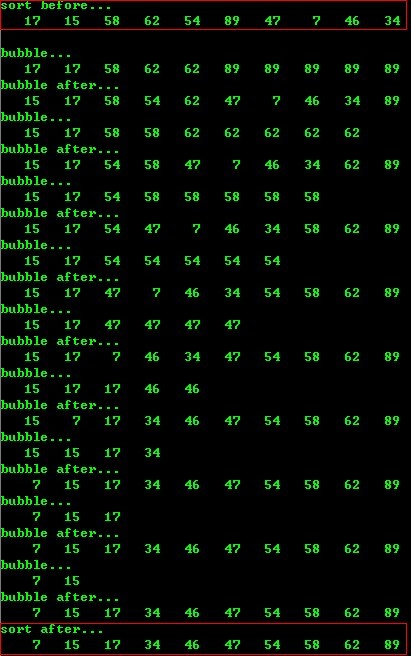
  26. void  sort( int  num[])  
  27. {  
  28.     int  i, j, tmp;  
  29.     for (i=1; i<MAX-1; i++)  
  30.     {  
  31.         printf("bubble.../n" );  
  32.         for (j=1; j<MAX-i; j++)  
  33.         {  
  34.             printf("%5d" , num[j]);  
  35.             if (num[j]>num[j+1])  
  36.             {  
  37.                 tmp=num[j];  
  38.                 num[j]=num[j+1];  
  39.                 num[j+1]=tmp;                                 
  40.             }  
  41.         }  
  42.         printf("%5d/n" , num[MAX-i]);  
  43.           
  44.         printf("bubble after.../n" );  
  45.         for (j=1; j<MAX; j++)  
  46.             printf("%5d" , num[j]);  
  47.         printf("/n" );  
  48.     }  
  49. }  
  50. /* bubble sort */   
  51. /*   
  52. void sort(int num[])  
  53. {  
  54.     int i, j, tmp;  
  55.     for(i=1; i<MAX-1; i++)  
  56.     {  
  57.         for(j=1; j<MAX-i; j++)  
  58.             if(num[j]>num[j+1])  
  59.             {  
  60.                 tmp=num[j];  
  61.                 num[j]=num[j+1];  
  62.                 num[j+1]=tmp;                                 
  63.             }  
  64.     }  
  65. }  
  66. */   
  67. void  main()  
  68. {  
  69.     int  num[MAX];  
  70.     printf("sort before.../n" );  
  71.     input(num);  
  72.     output(num);  
  73.     sort(num);  
  74.     printf("sort after.../n" );  
  75.     output(num);  
  76. }  

运行结果：

=======================================================

2、双向冒泡排序

据说可以提高效率，减少比较次数和交换次数

但仔细分析可得，每次while循环，都for循环比较了两次

因此每次low和high各减1，总体上比较次数并未减少，两次for交换也未减少

个人认为双向冒泡算法并未有效的减少比较次数和交换次数，但此算法也富含编程思想，值得学习

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include   
  2.  <stdio.h>  
  3. #include <stdlib.h>   
  4. #include <time.h>   
  5. #define swap(x, y){int tmp; tmp=x; x=y; y=tmp;}   
  6. #define MAX 11   
  7. void  input( int  num[])  
  8. {  
  9.     int  i;  
  10.       
  11.     srand((unsigned)time(NULL));  
  12.     for (i=1; i<MAX; i++)  
  13.         num[i]=rand()%100;  
  14. }  
  15. void  output( int  num[])  
  16. {  
  17.     int  i;  
  18.       
  19.     for (i=1; i<MAX; i++)  
  20.     {  
  21.         printf("%5d" , num[i]);  
  22.         if (0 == i%10)  
  23.             printf("/n" );  
  24.     }  
  25. }  
  26. void  sort( int  num[],  int  low,  int  high)  
  27. {  
  28.     int  i;  
  29.       
  30.     while (low<high)  
  31.     {  
  32.         for (i=low; i<high; i++)  /* bubble to high */   
  33.             if (num[i]>num[i+1])  
  34.                 swap(num[i], num[i+1]);  
  35.         high--;  
  36.           
  37.         for (i=high; i>low; i--)   /* bubble to low */   
  38.             if (num[i]<num[i-1])  
  39.                 swap(num[i], num[i-1]);  
  40.         low++;  
  41.     }  
  42. }  
  43. void  main()  
  44. {  
  45.     int  num[MAX];  
  46.     input(num);  
  47.       
  48.     printf("sort before.../n" );  
  49.     output(num);  
  50.       
  51.     sort(num, 1, MAX-1);  
  52.     printf("sort after.../n" );  
  53.     output(num);  
  54. }  

运行结果：

=======================================================

3、选择排序

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <stdlib.h>   
  3. #include <time.h>   
  4. #define MAX 101   
  5. void  input( int  num[])  
  6. {  
  7.     int  i;  
  8.       
  9.     srand((unsigned)time(NULL));  
  10.     for (i=1; i<MAX; i++)  
  11.         num[i]=rand()%100;        
  12. }  
  13. void  output( int  num[])  
  14. {  
  15.     int  i;  
  16.       
  17.     for (i=1; i<MAX; i++)  
  18.     {  
  19.         printf("%5d" , num[i]);  
  20.         if (0 == i%10)  
  21.             printf("/n" );  
  22.     }  
  23.     printf("/n" );  
  24. }  
  25. void  sort( int  num[])  
  26. {  
  27.     int  i, j, k, tmp;  
  28.     for (i=1; i<MAX-1; i++)  
  29.     {  
  30.         k=i;  
  31.         for (j=i+1; j<MAX; j++)  
  32.             if (num[k]>num[j])  
  33.                 k=j;  
  34.         if (i<k)  
  35.         {  
  36.             tmp=num[i];  
  37.             num[i]=num[k];  
  38.             num[k]=tmp;  
  39.         }  
  40.     }  
  41. }  
  42. void  main()  
  43. {  
  44.     int  num[MAX];  
  45.     printf("sort before.../n" );  
  46.     input(num);  
  47.     output(num);  
  48.     sort(num);  
  49.     printf("sort after.../n" );  
  50.     output(num);  
  51. }  

运行结果：

=======================================================

中级排序算法

向部分已排好序数列插入新值，使整个数列最终都有序

1、直接插入排序

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <stdlib.h>   
  3. #include <time.h>   
  4. #define MAX 11   
  5. void  input( int  num[])  
  6. {  
  7.     int  i;  
  8.       
  9.     srand((unsigned)time(NULL));  
  10.     for (i=1; i<MAX; i++)  
  11.         num[i]=rand()%100;        
  12. }  
  13. void  output( int  num[])  
  14. {  
  15.     int  i;  
  16.       
  17.     for (i=1; i<MAX; i++)  
  18.     {  
  19.         printf("%5d" , num[i]);  
  20.         if (0 == i%10)  
  21.             printf("/n" );  
  22.     }  
  23.     printf("/n" );  
  24. }  
  25. void  sort( int  num[])  
  26. {  
  27.     int  i, pos, tmp;  
  28.     for (i=2; i<MAX; i++)  /* from 2 to sorting */   
  29.     {  
  30.         pos=i;  
  31.         tmp=num[pos];  
  32.         while (pos>1 && tmp<num[pos-1])  
  33.         {             
  34.             num[pos]=num[pos-1];  
  35.             pos--;            
  36.         }  
  37.         num[pos]=tmp;  
  38.     }  
  39. }  
  40. void  main()  
  41. {  
  42.     int  num[MAX];  
  43.     printf("sort before.../n" );  
  44.     input(num);  
  45.     output(num);  
  46.     sort(num);  
  47.     printf("sort after.../n" );  
  48.     output(num);  
  49. }  

运行结果：

=======================================================

2、 折半插入排序

折半插入排序算法是一种稳定的排序算法，比直接插入算法明显减少了关键字之间比较的次数

因此速度比直接插入排序算法快，但记录移动的次数没有变，

所以折半插入排序算法的时间复杂度仍然为O(n^2)，


测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include   
  2.  <stdio.h>  
  3. #include <stdlib.h>   
  4. #include <time.h>   
  5. #define MAX 11   
  6. void  input( int  num[])  
  7. {  
  8.     int  i;  
  9.       
  10.     srand((unsigned)time(NULL));  
  11.     for (i=1; i<MAX; i++)  
  12.         num[i]=rand()%100;  
  13. }  
  14. void  output( int  num[])  
  15. {  
  16.     int  i;  
  17.       
  18.     for (i=1; i<MAX; i++)  
  19.     {  
  20.         printf("%5d" , num[i]);  
  21.         if (0 == i%10)  
  22.             printf("/n" );  
  23.     }  
  24.     printf("/n" );  
  25. }  
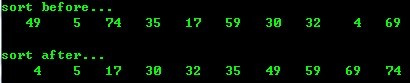
  26. void  sort( int  num[],  int  low,  int  high)  
  27. {  
  28.     int  i, j, mid;  
  29.     int  l, h;  
  30.     for (i=2; i<=high; i++)  
  31.     {  
  32.         l=low;  
  33.         h=i-1;  
  34.         num[0]=num[i]; /* save */   
  35.           
  36.         while (l<=h)  
  37.         {  
  38.             mid=(l+h)/2;  
  39.             if (num[0]<num[mid])  
  40.                 h=mid-1;  
  41.             else   
  42.                 l=mid+1;  
  43.         }  
  44.           
  45.         for (j=i; j>l; j--)   /* move */   
  46.             num[j]=num[j-1];  
  47.         num[l]=num[0];  
  48.     }  
  49. }  
  50. void  main()  
  51. {  
  52.     int  num[MAX];  
  53.       
  54.     input(num);  
  55.       
  56.     printf("sort before.../n" );  
  57.     output(num);  
  58.     sort(num, 1, MAX-1);  
  59.       
  60.     printf("sort after.../n" );  
  61.     output(num);      
  62. }  

运行结果：

=======================================================

3、 2-路插入排序

2-路插入排序： 是在折半插入排序的基础上再次改进，其目的是减少排序过程中记录移动的次数

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <stdlib.h>   
  3. #include <time.h>   
  4. #define MAX 11   
  5. int  num2[MAX];  
  6. void  input( int  num[])  
  7. {  
  8.     int  i;  
  9.       
  10.     srand((unsigned)time(NULL));  
  11.     for (i=1; i<MAX; i++)  
  12.         num[i]=rand()%100;  
  13. }  
  14. void  output( int  num[])  
  15. {  
  16.     int  i;  
  17.       
  18.     for (i=1; i<MAX; i++)  
  19.     {  
  20.         printf("%5d" , num[i]);  
  21.         if (0 == i%10)  
  22.             printf("/n" );  
  23.     }  
  24.     printf("/n" );  
  25. }  
  26. void  bi_insertsort( int  num[],  int  len)  
  27. {  
  28.     int  i, j, pos, head, tail;  
  29.     head=tail=1;  
  30.     num2[1]=num[1];  
  31.     for (i=2; i<=len; i++)  
  32.     {  
  33.         if (num[i]>num2[1])   /* larger, save to tail */   
  34.         {  
  35.             for (j=tail; j>1; j--)  
  36.             {  
  37.                 if (num[i]<num2[j])  
  38.                     num2[j+1]=num2[j];  
  39.                 else   
  40.                     break ;  
  41.             }  
  42.             num2[j+1]=num[i];  
  43.             tail++;  
  44.         }   
  45.         else      /* smaller, save to head */   
  46.         {  
  47.             if (head==1)    /* first to end, then to head... */   
  48.             {  
  49.                 num2[len]=num[i];  
  50.                 head=len;  
  51.             }  
  52.             else   
  53.             {  
  54.                 for (j=head; j<=len; j++)  
  55.                 {  
  56.                     if (num[i]>num2[j])  
  57.                         num2[j-1]=num2[j];  
  58.                     else   
  59.                         break ;  
  60.                 }  
  61.                 num2[j-1]=num[i];  
  62.                 head--;  
  63.             }  
  64.         }         
  65.     }  
  66.       
  67.     pos=1;  
  68.     for (i=1; i<=len; i++)  /* move back data from num2[] to num[] */   
  69.     {  
  70.         if (head<=len)  
  71.             num[i]=num2[head++];  
  72.         else   if (pos<=tail)  
  73.             num[i]=num2[pos++];  
  74.     }  
  75. }  
  76. int  main()  
  77. {  
  78.     int  num[MAX];  /* 1 - len is num, 0->null */   
  79.     input(num);  
  80.     printf("sort before.../n" );  
  81.     output(num);  
  82.       
  83.     bi_insertsort(num, MAX-1);  
  84.     printf("sort after.../n" );  
  85.     output(num);  
  86.       
  87.     return  0;  
  88. }  

运行结果：

=======================================================

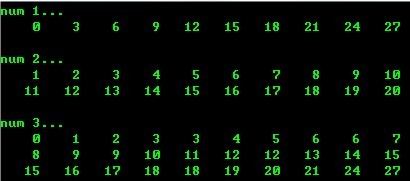
4、合并插入排序（数组实现）

将两个有序数组A、B合并成另一个有序的大数组C

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. void  input_num1( int  num[],  int  n1)  
  3. {  
  4.     int  i;  
  5.     for (i=1; i<=n1; i++)  
  6.         num[i]=3*(i-1);  
  7.     printf("/nnum 1.../n" );  
  8.     for (i=1; i<=n1; i++)  
  9.     {  
  10.         printf("%5d" , num[i]);  
  11.         if (0 == i%10)  
  12.             printf("/n" );  
  13.     }  
  14. }  
  15. void  input_num2( int  num[],  int  n2)  
  16. {  
  17.     int  i;  
  18.     for (i=1; i<=n2; i++)  
  19.         num[i]=i;  
  20.     printf("/nnum 2.../n" );  
  21.     for (i=1; i<=n2; i++)  
  22.     {  
  23.         printf("%5d" , num[i]);  
  24.         if (0 == i%10)  
  25.             printf("/n" );  
  26.     }  
  27. }  
  28. void  output_num3( int  num1[],  int  n1,  int  num2[],  int  n2,  int  num3[],  int  n3)  
  29. {  
  30.     int  pos1, pos2, pos3;  
  31.     pos3=pos2=pos1=1;  
  32.       
  33.     while (pos1<=n1 && pos2<=n2)  
  34.     {  
  35.         if (num1[pos1]<num2[pos2])  
  36.             num3[pos3++]=num1[pos1++];  
  37.         else   
  38.             num3[pos3++]=num2[pos2++];  
  39.     }  
  40.     while (pos1<=n1)  
  41.         num3[pos3++]=num1[pos1++];  
  42.     while (pos2<=n2)  
  43.         num3[pos3++]=num2[pos2++];  
  44.     printf("/n/nnum 3.../n" );  
  45.     for (pos3=1; pos3<=n3; pos3++)  
  46.     {  
  47.         printf("%5d" , num3[pos3]);  
  48.         if (0 == pos3%10)  
  49.             printf("/n" );  
  50.     }  
  51. }  
  52. void  main()  
  53. {  
  54.     int  num1[11];  
  55.     int  num2[21];  
  56.     int  num3[31];  
  57.       
  58.     input_num1(num1, 10);  
  59.     input_num2(num2, 20);  
  60.     output_num3(num1, 10, num2, 20, num3, 30);  
  61. }  

运行结果：

=======================================================

5、合并插入排序（链表实现）

将两个有序链表A、B合并成另一个有序的大链表C（链表单元来自A和B）

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <malloc.h>   
  3. struct  _link  
  4. {  
  5.     int  data;  
  6.     struct  _link *next;  
  7. };  
  8. typedef   struct  _link link, *plink;  
  9. plink init_link()  
  10. {  
  11.     plink p;  
  12.       
  13.     p=(plink)malloc(sizeof (link));  
  14.     if (!p)  /* if(p == NULL) */   
  15.     {  
  16.         printf("Error. malloc fail.../n" );  
  17.         return  NULL;  
  18.     }  
  19.     p->data=-1;  
  20.     p->next=NULL;  
  21.     return  p;  
  22. }  
  23. plink input_num1(plink plk, int  n1)  
  24. {  
  25.     int  i, count;  
  26.     plink p, s;  
  27.       
  28.     p=plk;  
  29.       
  30.     for (i=1; i<=n1; i++)  
  31.     {  
  32.         s=(plink)malloc(sizeof (link));  
  33.         if (!s)  /* if(p == NULL) */   
  34.         {  
  35.             printf("Error. malloc fail.../n" );  
  36.             return  NULL;  
  37.         }  
  38.         s->data=3*(i-1);  
  39.         s->next=NULL;  
  40.         p->next=s;  
  41.         p=p->next;  
  42.     }             
  43.       
  44.     count=0;  
  45.     s=plk->next;  
  46.     while (s)  
  47.     {  
  48.         count++;  
  49.         printf("%5d" , s->data);  
  50.         s=s->next;  
  51.         if (0 == count%10)  
  52.             printf("/n" );  
  53.     }  
  54.     printf("/n" );  
  55.     return  plk;  
  56. }  
  57. plink input_num2(plink plk, int  n2)  
  58. {  
  59.     int  i, count;  
  60.     plink p, s;  
  61.       
  62.     p=plk;  
  63.       
  64.     for (i=1; i<=n2; i++)  
  65.     {  
  66.         s=(plink)malloc(sizeof (link));  
  67.         if (!s)  /* if(p == NULL) */   
  68.         {  
  69.             printf("Error. malloc fail.../n" );  
  70.             return  NULL;  
  71.         }  
  72.         s->data=i;  
  73.         s->next=NULL;  
  74.         p->next=s;  
  75.         p=p->next;  
  76.     }             
  77.       
  78.     count=0;  
  79.     s=plk->next;  
  80.     while (s)  
  81.     {  
  82.         count++;  
  83.         printf("%5d" , s->data);  
  84.         s=s->next;  
  85.         if (0 == count%10)  
  86.             printf("/n" );  
  87.     }  
  88.     printf("/n" );  
  89.     return  plk;  
  90. }  
  91. void  output_num3(plink plk1, plink plk2, plink plk3)  
  92. {  
  93.     int  count;  
  94.     plink p1, p2, p3;  
  95.     p1=plk1->next;  
  96.     p2=plk2->next;  
  97.     p3=plk3;  
  98.     while (p1 && p2)  
  99.     {         
  100.         if (p1->data < p2->data)  
  101.         {  
  102.             p3->next=p1;  
  103.             p3=p3->next;  
  104.             p1=p1->next;  
  105.         }  
  106.         else   
  107.         {  
  108.             p3->next=p2;  
  109.             p3=p3->next;  
  110.             p2=p2->next;  
  111.         }  
  112.     }  
  113.     p3->next = p1 ? p1 : p2; /* NOTE: directly link to not NULL address, OK */   
  114.     count=0;  
  115.     p3=plk3->next;  
  116.     while (p3)  
  117.     {  
  118.         count++;  
  119.         printf("%5d" , p3->data);  
  120.         p3=p3->next;  
  121.         if (0 == count%10)  
  122.             printf("/n" );  
  123.     }  
  124.     printf("/n" );  
  125. }  
  126. void  main()  
  127. {  
  128.     plink plk1, plk2, plk3;  
  129.       
  130.     plk1=init_link();  
  131.     plk2=init_link();  
  132.     plk3=init_link();  
  133.     printf("num 1.../n" );  
  134.     plk1=input_num1(plk1, 10);  
  135.     printf("num 2.../n" );  
  136.     plk2=input_num2(plk2, 20);  
  137.       
  138.     printf("num 3.../n" );  
  139.     output_num3(plk1, plk2, plk3);  
  140. }  

运行结果：

=======================================================

高级排序算法

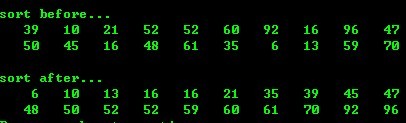
1、 快速排序

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <stdlib.h>   
  3. #include <time.h>   
  4. #define MAX 21   
  5. void  input( int  num[])  
  6. {  
  7.     int  i;  
  8.       
  9.     srand(time(NULL));  
  10.     for (i=0; i<MAX; i++)  
  11.         num[i]=rand()%100;  
  12. }  
  13. void  output( int  num[])  
  14. {  
  15.     int  i;  
  16.       
  17.     for (i=1; i<MAX; i++)  
  18.     {  
  19.         printf("%5d" , num[i]);  
  20.         if (0 == i%10)  
  21.             printf("/n" );  
  22.     }  
  23. }  
  24. void  sort( int  num[],  int  low,  int  high)  
  25. {  
  26.     int  l, h;  
  27.     l=low;  
  28.     h=high;  
  29.     if (low < high)  
  30.     {  
  31.         num[0]=num[l]; /* num[0] save pivot */   
  32.           
  33.         while (l<h)  
  34.         {  
  35.             while (l<h && num[h]>=num[0]) h--;  
  36.             num[l]=num[h];  
  37.             while (l<h && num[l]<=num[0]) l++;  
  38.             num[h]=num[l];  
  39.         }  
  40.         num[l]=num[0];  
  41.         sort(num, low, l-1);  
  42.         sort(num, l+1, high);  
  43.     }     
  44. }  
  45. void  main()  
  46. {  
  47.     int  num[MAX];  
  48.     input(num);  
  49.     printf("/nsort before.../n" );  
  50.     output(num);  
  51.     sort(num, 1, MAX-1);  
  52.     printf("/nsort before.../n" );  
  53.     output(num);  
  54. }  

运行结果：

=======================================================

2、 希尔排序

说明：本示例仅测试10或11个数的3趟希尔排序

由于希尔排序的增量step至今尚无精准的数学论证，无法给出科学、高效的序列函数

据严蔚敏的《数据结构（C语言版）》介绍说：希尔排序的分析是一个复杂的问题，因为它的时间是所取“增量”序列的函数，这涉及一些数学上尚未解决的难题（P272）.

因此，本示例仅是实际问题实际解决的一个特例。

本算法基本思想仍是上述直接排序算法的改进，仅仅步长由1变成了step而已

如果大家想需要增添或减少数组元素个数，请一并修改input（）函数中的step等趟数序列

如果大家对希尔排序算法有更好的改进，或有较好步长的函数和通用模板，希望能拿出来共同学习交流分享，谢谢！

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <stdlib.h>   
  3. #include <time.h>   
  4. #define MAX 11   /* num[] */   
  5. #define STEP 4   /* jump[] */   
  6. void  input( int  num[],  int  jump[])  
  7. {  
  8.     int  i;  
  9.     srand((unsigned)time(NULL));  
  10.     for (i=1; i<MAX; i++)  
  11.         num[i]=rand()%100;    
  12.     for (i=1; i<STEP; i++)  
  13.         jump[i]=7-2*i;   /* 1->5; 2->3; 3->1 */   
  14. }  
  15. void  output( int  num[])  
  16. {  
  17.     int  i;  
  18.       
  19.     for (i=1; i<MAX; i++)  
  20.     {  
  21.         printf("%5d" , num[i]);  
  22.         if (0 == i%10)  
  23.             printf("/n" );  
  24.     }  
  25. }  
  26. void  sort( int  num[],  int  jump[])  
  27. {  
  28.     int  i, j, pos, step;  
  29.     for (i=1; i<STEP; i++)  
  30.     {  
  31.         step=jump[i];  
  32.         for (j=1+step; j<MAX; j++)  
  33.         {  
  34.             pos=j;  
  35.             num[0]=num[pos]; /* save num[j] where (i+step)<j<MAX */   
  36.             while (num[0]<num[pos-step])  
  37.             {  
  38.                 num[pos]=num[pos-step];           
  39.                 pos=pos-step; /* shell: jump step */   
  40.             }  
  41.             num[pos]=num[0];  
  42.         }  
  43.     }  
  44. }  
  45. void  main()  
  46. {  
  47.     int  num[MAX];  
  48.     int  jump[STEP];  
  49.       
  50.     input(num, jump);  
  51.     printf("sort before.../n" );  
  52.     output(num);  
  53.     sort(num, jump);  
  54.       
  55.     printf("sort after.../n" );  
  56.     output(num);  
  57. }  

运行结果：

=======================================================

2、 希尔排序（网摘）

在学习希尔排序算法时，看到网上有如下一段希尔排序代码，也可以直接运行

但看代码来真得很费解，感觉变量定义不够直观，算法设计也不太简洁

因此，在最大程度保留源代码时，仅对变量名和算法逻辑简单修改

力争做到变量名清晰，逻辑顺畅，达到不用注释读者也能看明白

希望对大家学习有点帮助

测试环境：VC 6.0 (C)

摘录原代码：http://apps.hi.baidu.com/share/detail/5669244（百度空间）

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <iostream.h>   
  2. void  ShellSort( int * pData, int  Count)  
  3. {  
  4.    int  step[4];  
  5.    step[0] = 9;  
  6.    step[1] = 5;  
  7.    step[2] = 3;  
  8.    step[3] = 1;  
  9.    int  iTemp;  
  10.    int  k,s,w;  
  11.    for ( int  i=0;i<4;i++)  
  12.    {  
  13.      k = step[i];  
  14.      s = -k;  
  15.      for ( int  j=k;j<Count;j++)  
  16.      {  
  17.        iTemp = pData[j];  
  18.        w = j-k;//求上step个元素的下标   
  19.        if (s ==0)  
  20.        {  
  21.          s = -k;  
  22.          s++;  
  23.          pData[s] = iTemp;  
  24.        }  
  25.        while ((iTemp<pData[w]) && (w>=0) && (w<=Count))  
  26.        {  
  27.          pData[w+k] = pData[w];  
  28.          w = w-k;  
  29.        }  
  30.        pData[w+k] = iTemp;  
  31.      }  
  32.    }  
  33. }  
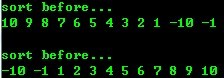
  34. void  main()  
  35. {  
  36.    int  data[] = {10,9,8,7,6,5,4,3,2,1,-10,-1};  
  37.    ShellSort(data,12);  
  38.    for  ( int  i=0;i<12;i++)  
  39.      cout<<data[i]<<" " ;  
  40.    cout<<"/n" ;  
  41. }  
 

修改后代码：

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <iostream.h>    
  2. void  ShellSort( int * pData, int  Count)   
  3. {     
  4.     int  iTemp;   
  5.     int  steplen, pos;  
  6.     int  step[4];   
  7.     step[0] = 9;   
  8.     step[1] = 5;   
  9.     step[2] = 3;   
  10.     step[3] = 1;   
  11.       
  12.     for ( int  i=0;i<4;i++)   
  13.     {   
  14.         steplen = step[i];   
  15.         for ( int  j=0+steplen; j<Count; j++)   
  16.         {   
  17.             iTemp = pData[j];   
  18.             pos=j;  
  19.             while (iTemp<pData[pos-steplen] && pos>0)   
  20.             {   
  21.                 pData[pos] = pData[pos-steplen];   
  22.                 pos=pos-steplen;  
  23.             }   
  24.             pData[pos] = iTemp;   
  25.         }   
  26.     }   
  27. }   
  28. void  main()   
  29. {   
  30.     int  data[] = {10,9,8,7,6,5,4,3,2,1,-10,-1};   
  31.     cout<<endl<<"sort before..." <<endl;   
  32.     for  ( int  i=0;i<12;i++)   
  33.         cout<<data[i]<<" " ;   
  34.     cout<<endl;   
  35.     ShellSort(data,12);   
  36.     cout<<endl<<"sort before..." <<endl;   
  37.     for  (i=0;i<12;i++)   
  38.         cout<<data[i]<<" " ;   
  39.     cout<<endl;   
  40. }  

运行结果：

=======================================================

3、 堆排序

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <stdlib.h>   
  3. #include <time.h>   
  4. #define MAX 11   
  5. void  input( int  num[])  
  6. {  
  7.     int  i;  
  8.       
  9.     srand((unsigned)time(NULL));  
  10.     for (i=1; i<MAX; i++)  
  11.         num[i]=rand()%100;  
  12. }  
  13. void  output( int  num[])  
  14. {  
  15.     int  i;  
  16.       
  17.     for (i=1; i<MAX; i++)  
  18.     {  
  19.         printf("%5d" , num[i]);  
  20.         if (0 == i%10)  
  21.             printf("/n" );  
  22.     }  
  23.     printf("/n" );  
  24. }  
  25. void  heapadjust( int  num[],  int  s,  int  len)  /* build large heap */   
  26. {  
  27.     int  j;  
  28.     num[0]=num[s];  /* save temp data */   
  29.       
  30.     for (j=2*s; j<=len; j*=2)  
  31.     {  
  32.         if (j<len && num[j]<num[j+1])  /* num[j+1] is limited by j<len beyond the border */   
  33.             j++;  
  34.         if (num[0]>num[j])  
  35.             break ;  
  36.         num[s]=num[j];  
  37.         s=j;  
  38.     }  
  39.     num[s]=num[0];  
  40. }  
  41. void  heapsort( int  num[],  int  len)  
  42. {  
  43.     int  i, tmp;  
  44.     for (i=len/2; i>0; i--)  /* build heap */   
  45.         heapadjust(num, i, len);  
  46.       
  47.     for (i=len; i>1; i--)    /* sort heap */   
  48.     {  
  49.         tmp=num[1];    /* change largest data to end */   
  50.         num[1]=num[i];  
  51.         num[i]=tmp;  
  52.         heapadjust(num, 1, i-1); /* rebuild large heap for (i-1) data */   
  53.     }  
  54. }  
  55. int  main()  
  56. {  
  57.     int  num[MAX];  /* 1 - len is num, 0->null */   
  58.     input(num);  
  59.     printf("sort before.../n" );  
  60.     output(num);  
  61.       
  62.     heapsort(num, MAX-1);  
  63.     printf("sort after.../n" );  
  64.     output(num);  
  65.       
  66.     return  0;  
  67. }  

运行结果：

=======================================================

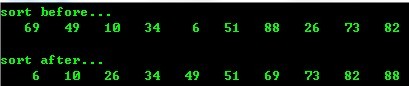
4、 归并排序

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <stdlib.h>   
  3. #include <time.h>   
  4. #define MAX 11   
  5. int  num2[MAX];  /* copy array */   
  6. void  input( int  num[])  
  7. {  
  8.     int  i;  
  9.       
  10.     srand((unsigned)time(NULL));  
  11.     for (i=1; i<MAX; i++)  
  12.         num[i]=rand()%100;  
  13. }  
  14. void  output( int  num[])  
  15. {  
  16.     int  i;  
  17.       
  18.     for (i=1; i<MAX; i++)  
  19.     {  
  20.         printf("%5d" , num[i]);  
  21.         if (0 == i%10)  
  22.             printf("/n" );  
  23.     }  
  24.     printf("/n" );  
  25. }  
  26. void  merge( int  num[],  int  low,  int  mid,  int  high)  
  27. {  
  28.     int  l, h, i, j;  
  29.     l=low;  
  30.     h=high;  
  31.     for (i=mid+1, j=low; low<=mid && i<=high; j++)  
  32.     {  
  33.         if (num[low]<num[i])  
  34.             num2[j]=num[low++];  
  35.         else   
  36.             num2[j]=num[i++];  
  37.     }  
  38.     if (low<=mid)  
  39.         for (; j<=high; j++, low++)  
  40.             num2[j]=num[low];  
  41.     if (i<=high)  
  42.         for (; j<=high; j++, i++)  
  43.             num2[j]=num[i];  
  44.     for (i=l; i<=h; i++)  
  45.         num[i]=num2[i];  
  46. }  
  47. void  mergesort( int  num[],  int  low,  int  high)  
  48. {  
  49.     int  mid;  
  50.     if (low==high)  
  51.         num2[low]=num[low];  
  52.     else   
  53.     {  
  54.         mid=(low+high)/2;  
  55.         mergesort(num, low, mid);     /* to low */   
  56.         mergesort(num, mid+1, high);  /* to high */   
  57.         merge(num, low, mid, high);   /* recursion */   
  58.     }  
  59. }  
  60. int  main()  
  61. {  
  62.     int  num[MAX];  /* 1 - len is num, 0->null */   
  63.     input(num);  
  64.     printf("sort before.../n" );  
  65.     output(num);  
  66.       
  67.     mergesort(num, 1, MAX-1);  
  68.     printf("sort after.../n" );  
  69.     output(num);  
  70.       
  71.     return  0;  
  72. }  

运行结果：

=======================================================

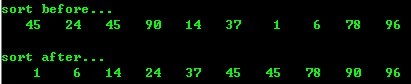
排序算法的知识扩展（网摘）

内部排序算法的比较和实现
引用网址： http://www.cppblog.com/feosun/archive/2008/10/12/63831.html（直接摘录，尚未测试）

参考网址： http://sjjp.tjuci.edu.cn/sjjg/DataStructure/DS/web/paixu/paixu8.1.1.1.htm（数据结构）


排序是数据处理中经常使用的一种重要运算,在计算机及其应用系统中,花费在排序上的时间在系统运行时间中占有很大比重;并且排序本身对推动算法分析的发展 也起很大作用。目前已有上百种排序方法，但尚未有一个最理想的尽如人意的方法，本文介绍常用的如下排序方法的C/C++实现，并对它们进行分析和比较。

选择排序、快速排序、希尔排序、堆排序不是稳定的排序算法，而冒泡排序、插入排序、归并排序和基数排序是稳定的排序算法。

首先，排序算法的稳定性大家应该都知道，通俗地讲就是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。在简单形式化一下，如果Ai = Aj, Ai原来在位置前，排序后Ai还是要在Aj位置前。

其次，说一下稳定性的好处。排序算法如果是稳定的，那么从一个键上排序，然后再从另一个键上排序，第一个键排序的结果可以为第二个键排序所用。基数排序就 是这样，先按低位排序，逐次按高位排序，低位相同的元素其顺序再高位也相同时是不会改变的。另外，如果排序算法稳定，对基于比较的排序算法而言，元素交换 的次数可能会少一些(个人感觉，没有证实)。

回到主题，现在分析一下常见的排序算法的稳定性，每个都给出简单的理由。

(1)冒泡排序
        冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较，交换也发生在这两个元素之间。所以，如果两个元素相等，我想你是不会再无 聊地把他们俩交换一下的；如果两个相等的元素没有相邻，那么即使通过前面的两两交换把两个相邻起来，这时候也不会交换，所以相同元素的前后顺序并没有改 变，所以冒泡排序是一种稳定排序算法。

(2)选择排序
      选择排序是给每个位置选择当前元素最小的，比如给第一个位置选择最小的，在剩余元素里面给第二个元素选择第二小的，依次类推，直到第n-1个元素，第n个 元素不用选择了，因为只剩下它一个最大的元素了。那么，在一趟选择，如果当前元素比一个元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么 交换后稳定性就被破坏了。比较拗口，举个例子，序列5 8 5 2 9，我们知道第一遍选择第1个元素5会和2交换，那么原序列中2个5的相对前后顺序就被破坏了，所以选择排序不是一个稳定的排序算法。

(3)插入排序
     插入排序是在一个已经有序的小序列的基础上，一次插入一个元素。当然，刚开始这个有序的小序列只有1个元素，就是第一个元素。比较是从有序序列的末尾开 始，也就是想要插入的元素和已经有序的最大者开始比起，如果比它大则直接插入在其后面，否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相 等的，那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳 定的。

(4)快速排序
    快速排序有两个方向，左边的i下标一直往右走，当a[i] <= a[center_index]，其中center_index是中枢元素的数组下标，一般取为数组第0个元素。而右边的j下标一直往左走，当a[j] > a[center_index]。如果i和j都走不动了，i <= j, 交换a[i]和a[j],重复上面的过程，直到i>j。交换a[j]和a[center_index]，完成一趟快速排序。在中枢元素和a[j]交 换的时候，很有可能把前面的元素的稳定性打乱，比如序列为 5 3 3 4 3 8 9 10 11，现在中枢元素5和3(第5个元素，下标从1开始计)交换就会把元素3的稳定性打乱，所以快速排序是一个不稳定的排序算法，不稳定发生在中枢元素和 a[j] 交换的时刻。

(5)归并排序
    归并排序是把序列递归地分成短序列，递归出口是短序列只有1个元素(认为直接有序)或者2个序列(1次比较和交换),然后把各个有序的段序列合并成一个有 序的长序列，不断合并直到原序列全部排好序。可以发现，在1个或2个元素时，1个元素不会交换，2个元素如果大小相等也没有人故意交换，这不会破坏稳定 性。那么，在短的有序序列合并的过程中，稳定是是否受到破坏？没有，合并过程中我们可以保证如果两个当前元素相等时，我们把处在前面的序列的元素保存在结 果序列的前面，这样就保证了稳定性。所以，归并排序也是稳定的排序算法。

(6)基数排序
   基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优 先级排序，最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。基数排序基于分别排序，分别收集，所以其是稳定的排序算法。

(7)希尔排序(shell)
    希尔排序是按照不同步长对元素进行插入排序，当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了，步长很小， 插入排序对于有序的序列效率很高。所以，希尔排序的时间复杂度会比o(n^2)好一些。由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元 素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。

(8)堆排序
   我们知道堆的结构是节点i的孩子为2*i和2*i+1节点，大顶堆要求父节点大于等于其2个子节点，小顶堆要求父节点小于等于其2个子节点。在一个长为n 的序列，堆排序的过程是从第n/2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n /2-1, n/2-2, ...1这些个父节点选择元素时，就会破坏稳定性。有可能第n/2个父节点交换把后面一个元素交换过去了，而第n/2-1个父节点把后面一个相同的元素没 有交换，那么这2个相同的元素之间的稳定性就被破坏了。所以，堆排序不是稳定的排序算法。

/*
   冒泡排序  插入排序 二路插入排序 希尔排序   快速排序 选择排序 归并排序  堆排序算法的
   C/C++实现。
  
   作者：feosun

   日期：2008年10月12日

   参考资料：数据结构(C语言版) 清华大学出版社

*/

#include <iostream>
using namespace std;


//交换两个数的值
void swap(int &a,int &b)
{
    int tmp;
    tmp=a;
    a=b;
    b=tmp;
}

//屏幕输出数组
void display(int array[],int len)
{
    cout<<"the result is:"<<endl;
    for (int i = 0 ;i < len;i++ )
    {
        cout<<array[i]<<"  ";
    }
    cout<<endl;
}

/*
冒泡排序

算法思想：将被排序的记录数组R[1..n]垂直排列，每个记录R[i]看作是重量为R[i].key的气泡。
          根据轻气泡不能在重气泡之下的原则，从下往上扫描数组 R：凡扫描到违反本原则的
          轻气泡，就使其向上"飘浮"。如此反复进行，直到最后任何两个气泡都是轻者在上，
          重者在下为止。

时间复杂度 o(n^2)

空间复杂度 o(1)

比较次数 n(n+1)/2
*/
void bubble_sort(int array[],int len)
{
   
    for (int i = len-1 ;i >= 0;i-- )
    {
        for(int j = 0;j < i;j++)
            if(array[j] > array[j+1])
                swap(array[j],array[j+1]);
    }
}

/*
直接插入排序

算法思想：把n个待排序的元素看成为一个有序表和一个无序表，开始时有序表中只包含一个元
          素，无序表中包含有n-1个元素，排序过程中每次从无序表中取出第一个元素，将它
          插入到有序表中的适当位置，使之成为新的有序表，重复n-1次可完成排序过程。

时间复杂度 o(n^2)

空间复杂度 o(1)

比较次数 n(n+1)/2
*/
void insert_sort(int array[],int len)
{
    int tmp,i,j;

    for(i = 1;i < len;i++)
    {
        if (array[i] < array[i-1])
        {
            tmp = array[i];
            array[i] = array[i-1];

            //插入到相应位置
            for (j = i-2;j >= 0;j--)
            {
                //往后移
                    if (array[j] > tmp )
                        array[j+1] = array[j];
                    else
                    {
                        array[j+1] = tmp;
                        break;
                    }
            }
            if(j == -1)
            array[j+1] = tmp;
        }
    }
}

/*
2-路插入排序

算法思想：增加一个辅助空间d,把r[1]赋值给d[1]，并将d[1]看成是排好序后处于中间
          位置的记录。然后从r[2]开始依次插入到d[1]之前或之后的有序序列中。

时间复杂度 o(n^2)

空间复杂度 o(1)

比较次数 n(n+1)/2
*/

void bi_insert_sort(int array[],int len)
{
    int* arr_d = (int *)malloc(sizeof(int) * len);

    arr_d[0] = array[0];
    int head = 0,tail = 0;
    for (int i = 1;i < len; i++ )
    {
        if (array[i] > arr_d[0])
        {
            int j;
            for ( j= tail;j>0;j--)
            {
                if (array[i] < arr_d[j])
                    arr_d[j+1] = arr_d[j];
                else
                    break;
            }
            arr_d[j+1] = array[i];
            tail += 1;
        }

        else
        {
            if (head ==0)
            {
                arr_d[len-1] = array[i];
                head =len-1;
            }
            else
            {
                int j;
                for (j = head;j <= len-1;j++)
                {
                    if (array[i] > arr_d[j])
                        arr_d[j-1] = arr_d[j];
                    else
                        break;
                }
                arr_d[j-1] = array[i];
                head -= 1;
            }
        }

    }

    for (int i = 0;i < len; i++)
    {
        int pos = (i + head );
        if(pos >= len) pos -= len;
        array[i] = arr_d[pos];
    }

    free(arr_d);
}

/*
希尔排序

算法思想：先将整个待排序记录分割成若干子序列分别进行直接插入排
          序，待整个序列中的记录基本有序时，再对全体记录进行一
          次直接插入排序

时间复杂度 o(n^2)

空间复杂度 o(1)

比较次数 ?
*/

void shell_insert(int array[],int d,int len)
{
    int tmp,j;

    for (int i = d;i < len;i++)
    {
        if(array[i] < array[i-d])
        {
            tmp = array[i];
            j = i - d;
            do
            {
                array[j+d] = array[j];
                j = j - d;
            } while (j >= 0 && tmp < array[j]);

            array[j+d] = tmp;
        }
    }
}
void shell_sort(int array[],int len)
{
    int inc = len;

    do
    {
        inc = inc/2;
        shell_insert(array,inc,len);
    } while (inc > 1);
}

/*
快速排序

算法思想：将原问题分解为若干个规模更小但结构与原问题相似的子问题。递
          归地解这些子问题，然后将这些子问题的解组合成为原问题的解。

时间复杂度 o(nlogn)

空间复杂度 o(logn)

比较次数  ?
*/

int partition(int array[],int low,int high)
{
    int  pivotkey = array[low];

    while (low < high)
    {
        while(low < high && array[high] >= pivotkey)
            --high;
        swap(array[low],array[high]);

        while(low < high && array[low] <= pivotkey)
            ++low;
        swap(array[low],array[high]);
    }

    array[low] = pivotkey;

    return low;
}

void quick_sort(int array[],int low,int high)
{
    if (low < high)
    {
        int pivotloc = partition(array,low,high);
        quick_sort(array,low,pivotloc-1);
        quick_sort(array,pivotloc+1,high);
    }
}

/*
直接选择排序

算法思想：每一趟在n-i+1个记录中选取关键字最小的记录作为有序序列中的第i个记录

时间复杂度 o(n^2)

空间复杂度 o(1) ?

比较次数  n(n+1)/2
*/

int SelectMinKey(int array[],int iPos,int len)
{
    int ret = 0;

    for (int i = iPos; i < len; i++)
    {
        if (array[ret] > array[i])
        {
            ret = i;
        }
    }
    return ret;
}

void select_sort(int array[],int len)
{
    for (int i = 0; i < len; i++)
    {
        int j = SelectMinKey(array,i,len);
        if (i != j)
        {
            swap(array[i],array[j]);
        }
    }
}

/*
归并排序

算法思想：设两个有序的子文件(相当于输入堆)放在同一向量中相邻的位置上：R[low..m]，R[m+1..high]，先
          将它们合并到一个局部的暂存向量R1(相当于输出堆)中，待合并完成后将R1复制回R[low..high]中。

时间复杂度 o(nlogn)

空间复杂度 o(n)

比较次数  ?
*/

void merge(int array[],int i,int m, int n)
{
    int j,k;

    int iStart = i, iEnd = n;

    int arrayDest[256];

    for ( j = m + 1,k = i; i <= m && j <= n; ++k)
    {
        if (array[i] < array[j])
            arrayDest[k] = array[i++];
        else
            arrayDest[k] = array[j++];
    }

    if (i <= m)
        for (;k <= n; k++,i++)
            arrayDest[k] = array[i];
    if(j <= n)
        for (;k <= n; k++,j++)
            arrayDest[k] = array[j];

    for(j = iStart; j <= iEnd; j++)
        array[j] = arrayDest[j];
}

void merge_sort(int array[],int s,int t)
{
    int m;

    if (s < t)
    {
        m = (s + t )/2;
        merge_sort(array,s,m);
        merge_sort(array,m+1,t);
        merge(array,s,m,t);
    }
}

/*
堆排序

算法思想：堆排序（Heap Sort）是指利用堆（heaps）这种数据结构来构造的一种排序算法。
          堆是一个近似完全二叉树结构，并同时满足堆属性：即子节点的键值或索引总是
          小于（或者大于）它的父节点。
时间复杂度 o(nlogn)
空间复杂度 o(1)
比较次数  较多
*/

void heap_adjust(int array[],int i,int len)
{
    int rc = array[i];

    for(int j = 2 * i; j <len; j *= 2)
    {
        if(j < len && array[j] < array[j+1]) j++;
        if(rc >= array[j]) break;

        array[i] = array[j]; i = j;
    }
    array[i] = rc;
}

void heap_sort(int array[],int len)
{
    int i;
    for(i = (len-1)/2; i >= 0; i--)
        heap_adjust(array,i,len);
    for(  i = (len-1); i > 0; i--)
    {
        swap(array[0],array[i]);   //弹出最大值，重新对i-1个元素建堆
        heap_adjust(array,0,i-1);
    }
}

int main() {

    int array[] = {45,56,76,234,1,34,23,2,3,55,88,100};

    int len = sizeof(array)/sizeof(int);

    //bubble_sort(array,len);           //冒泡排序

    /*insert_sort(array,len);*/         //插入排序

    /*bi_insert_sort(array,len);*/      //二路插入排序
   
    /*shell_sort(array,len);*/          //希尔排序

    /*quick_sort(array,0,len-1);*/      //快速排序
   
    /*select_sort(array,len);*/         //选择排序

    /*merge_sort(array,0,len-1);*/      //归并排序
   
    heap_sort(array,len);               //堆排序
    display(array,len);

    return 0;
}

 

 

各种基本算法实现小结（六）—— 查找算法

（均已测试通过）

===================================================================

1、简单查找

在一组无序数列中，查找特定某个数值，并返回其位置pos

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <stdlib.h>   
  3. #include <time.h>   
  4. #define MAX 101   
  5. void  input( int  num[])  
  6. {  
  7.     int  i;  
  8.       
  9.     srand((unsigned)time(NULL));  
  10.     for (i=1; i<MAX; i++)  
  11.         num[i]=rand()%100;  
  12. }  
  13. void  output( int  num[])  
  14. {  
  15.     int  i;  
  16.       
  17.     for (i=1; i<MAX; i++)  
  18.     {  
  19.         printf("%5d" , num[i]);  
  20.         if (0==i%10)  
  21.             printf("/n" );  
  22.     }  
  23. }  
  24. int  find( int  num[],  int  x)  
  25. {  
  26.     int  i;  
  27.     for (i=1; i<MAX; i++)  
  28.         if (x == num[i])  
  29.             return  i;  
  30.     return  0;  
  31. }  
  32. void  main()  
  33. {  
  34.     int  x, pos, num[MAX];  
  35.     input(num);  
  36.       
  37.     printf("num...: /n" );  
  38.     output(num);  
  39.       
  40.     printf("Enter find num: " );  
  41.     scanf("%d" , &x);  
  42.     pos=find(num, x);  
  43.     if (pos)  
  44.         printf("OK! %d is found in pos: %d/n" , x, pos);  
  45.     else   
  46.         printf("Sorry! %d is not found... in num/n" , x);  
  47. }  

运行结果：

 

==========================================================

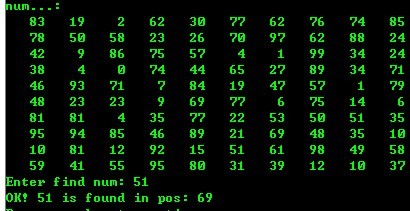
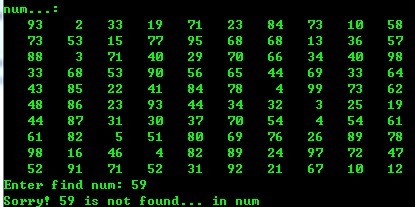
2、 折半查找

在有序数列中，逐步缩小查找范围，直至找到或找不到记录为止

本算法首先随机生成100个无序数列，然后利用快速排序算法排序成有序数列，然后再用折半查找算法

说明： 本算法中的排序算法，可用上一篇排序算法中的任一种算法实现，如选择排序、冒泡排序、快速排序等

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <stdlib.h>   
  3. #include <time.h>   
  4. #define MAX 101   
  5. void  input( int  num[])  
  6. {  
  7.     int  i;  
  8.       
  9.     srand((unsigned)time(NULL));  
  10.     for (i=1; i<MAX; i++)  
  11.         num[i]=rand()%100;  
  12. }  
  13. void  output( int  num[])  
  14. {  
  15.     int  i;  
  16.       
  17.     for (i=1; i<MAX; i++)  
  18.     {  
  19.         printf("%5d" , num[i]);  
  20.         if (0==i%10)  
  21.             printf("/n" );  
  22.     }  
  23. }  
  24. void  sort( int  num[],  int  low,  int  high)  /* quick sort */   
  25. {  
  26.     int  l, h;  
  27.       
  28.     if (low<high)  
  29.     {  
  30.         l=low;  
  31.         h=high;  
  32.         num[0]=num[l]; /* save pivot */   
  33.           
  34.         while (l<h)  
  35.         {  
  36.             while (l<h && num[h]>=num[0]) h--;  
  37.                 num[l]=num[h];  
  38.             while (l<h && num[l]<=num[0]) l++;  
  39.                 num[h]=num[l];  
  40.         }  
  41.         num[l]=num[0]; /* insert pivot */   
  42.           
  43.         sort(num, low, l-1);  
  44.         sort(num, l+1, high);  
  45.     }  
  46. }  
  47. int  find( int  num[],  int  x,  int  low,  int  high)  
  48. {  
  49.     int  mid;  
  50.       
  51.     while (low<=high)  
  52.     {  
  53.         mid=(low+high)/2; /* find is OK */   
  54.           
  55.         if (x==num[mid])  
  56.             return  mid;  
  57.         else   if (x<num[mid])  
  58.             high=mid-1;  
  59.         else   
  60.             low=mid+1;  
  61.     }  
  62.     return  0;  
  63. }  
  64. void  main()  
  65. {  
  66.     int  x, pos, num[MAX];  
  67.     input(num);  
  68.       
  69.     printf("sort before... /n" );  
  70.     output(num);  
  71.     sort(num, 1, MAX-1);  
  72.     printf("sort after... /n" );  
  73.     output(num);  
  74.       
  75.     printf("Enter find num: " );  
  76.     scanf("%d" , &x);  
  77.     pos=find(num, x, 1, MAX-1);  
  78.     if (pos)  
  79.         printf("OK! %d is found in pos: %d/n" , x, pos);  
  80.     else   
  81.         printf("Sorry! %d is not found... in num/n" , x);  
  82. }  

运行结果：

  

==========================================================

 

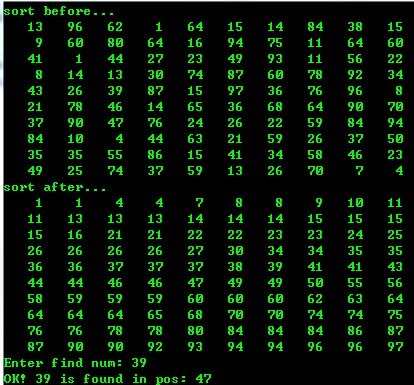
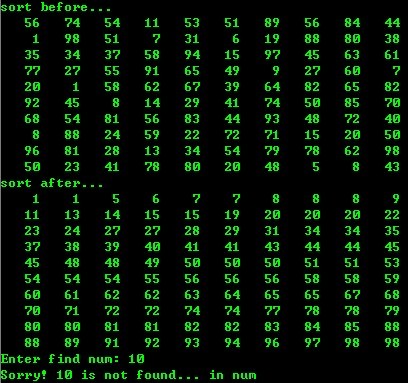
各种基本算法实现小结（七）—— 常用算法

（均已测试通过）

======================================================================

1、判断素数

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <math.h>   
  3. int  is_sushu( int  n)  
  4. {  
  5.     int  i, mid;  
  6.     mid=(int )sqrt(n);  
  7.     for (i=2; i<=mid; i++)  
  8.         if (0 == n%i)  
  9.             return  0;  
  10.     return  1;  
  11. }  
  12. void  main()  
  13. {  
  14.     int  n;  
  15.       
  16.     printf("Enter a num: " );  
  17.     scanf("%d" , &n);  
  18.     if (is_sushu(n))  
  19.         printf("%d is sushu!/n" , n);  
  20.     else   
  21.         printf("%d is not sushu.../n" , n);  
  22. }  

运行结果：

   

==========================================================

2、 求2-1000之间的所有素数

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <math.h>   
  3. #define MAX 1000   
  4. int  is_sushu( int  n)  
  5. {  
  6.     int  i, mid;  
  7.     mid=(int )sqrt(n);  
  8.     for (i=2; i<=mid; i++)  
  9.         if (0 == n%i)  
  10.             return  0;  
  11.     return  1;  
  12. }  
  13. void  main()  
  14. {  
  15.     int  i, count;  
  16.       
  17.     count=0;  
  18.       
  19.     for (i=2; i<=MAX; i++)  
  20.         if (is_sushu(i))  
  21.         {  
  22.             count++;  
  23.             printf("%5d" , i);  
  24.                 if (0 == count%10)  
  25.                     printf("/n" );  
  26.         }  
  27.     printf("/n" );  
  28. }  

运行结果：

==========================================================

3、 验证哥德巴赫猜想

哥德巴赫猜想： 任意一个大于等于6的偶数都可以分解为两个素数之和

如： 6 = 3+3；100 = 3+97=11+89； 1000 = 3+997=59+941=。。。

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <math.h>   
  3. #define MAX 1000   
  4. int  is_sushu( int  n)  
  5. {  
  6.     int  i, mid;  
  7.     mid=(int )sqrt(n);  
  8.     for (i=2; i<=mid; i++)  
  9.         if (0 == n%i)  
  10.             return  0;  
  11.     return  1;  
  12. }  
  13. void  main()  
  14. {  
  15.     int  i, mid, n;  
  16.       
  17.     printf("Enter an even num: " );  
  18.     scanf("%d" , &n);  
  19.       
  20.     mid=n/2;  
  21.     for (i=2; i<=mid; i++)  
  22.     {  
  23.         if (is_sushu(i) && is_sushu(n-i))  
  24.             printf("%d = %d + %d/n" , n, i, n-i);  
  25.     }  
  26.       
  27. }  

运行结果：

      

==========================================================

4、 求最大公约数（GCD）和最小公倍数(LCM)

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. void   max_min( int  &m,  int  &n)  
  3. {  
  4.     int  tmp;  
  5.     if (m<n)  
  6.     {  
  7.         tmp=m;  
  8.         m=n;  
  9.         n=tmp;  
  10.     }  
  11. }  
  12. int  Cal_GCD( int  m,  int  n)  
  13. {  
  14.     int  gcd;  
  15.       
  16.     max_min(m, n);  
  17.     gcd=m%n;  
  18.     while (gcd)  
  19.     {  
  20.         m=n;  
  21.         n=gcd;  
  22.         gcd=m%n;  
  23.     }  
  24.     return  n;  
  25. }  
  26. void  main()  
  27. {  
  28.     int  m, n, gcd;  
  29.       
  30.     printf("Enter two num a b: " );  
  31.     scanf("%d %d" , &m, &n);  
  32.     gcd=Cal_GCD(m, n);  
  33.     printf("%d and %d GCD: %d/n" , m, n, gcd);  
  34.     printf("%d and %d LCM: %d/n" , m, n, m*n/gcd);  
  35. }  

运行结果：

==========================================================

5、统计个数（数字）

用随机函数产生100个[0，99]范围内的随机整数，

统计个位上的数字分别为0，1，2，3，4，5，6，7，8，9的数的个数并打印出来

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <stdlib.h>   
  3. #include <time.h>   
  4. #include <string.h>   
  5. #define MAX 101   
  6. void  input( int  num[])  
  7. {  
  8.     int  i;  
  9.     srand((unsigned)time(NULL));  
  10.     for (i=1; i<MAX; i++)  
  11.         num[i]=rand()%100;  
  12. }  
  13. void  output( int  num[])  
  14. {  
  15.     int  i;  
  16.     for (i=1; i<MAX; i++)  
  17.     {  
  18.         printf("%5d" , num[i]);  
  19.         if (0==i%10)  
  20.             printf("/n" );  
  21.     }  
  22.     printf("/n" );  
  23. }  
  24. void  cal_num( int  num[],  int  count[])  
  25. {  
  26.     int  i, mod;  
  27.       
  28.     for (i=1; i<MAX; i++)  
  29.     {  
  30.         mod=num[i]%10;  
  31.         count[mod]++;  
  32.     }  
  33. }  
  34. void  main()  
  35. {  
  36.     int  num[MAX];  
  37.     int  i, count[10];  
  38.       
  39.     memset(count, 0, 10*sizeof ( int ));  /* initial count[] to 0 */   
  40.     input(num);  
  41.     printf("100 num:/n" );  
  42.     output(num);  
  43.       
  44.     cal_num(num, count);  
  45.     for (i=0; i<10; i++)  
  46.         printf("%d: %d/n" , i, count[i]);      
  47. }  

运行结果：

==========================================================

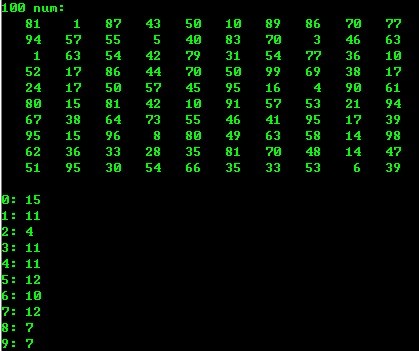
6、统计个数（数字、字符、其它字符）

输入一行字符，统计其中有多少个数字、字符和其它字符

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <string.h>   
  3. #define MAX 1024   
  4. void  cal_num( char  *str,  int  count[])  
  5. {  
  6.     char  *pstr;  
  7.     pstr=str;  
  8.     while (*pstr)  /* *pstr != 0 */   
  9.     {  
  10.         if (*pstr>= '0'  && *pstr<= '9' )  
  11.             count[0]++;  
  12.         else   if ((*pstr>= 'a'  && *pstr<= 'z' ) || (*pstr>= 'A'  && *pstr<= 'Z' ))  
  13.             count[1]++;  
  14.         else   
  15.             count[2]++;  
  16.           
  17.         pstr++;  
  18.     }  
  19. }  
  20. void  main()  
  21. {  
  22.     char  str[MAX];  
  23.     int  i, count[3];   /* 0->num; 1->char; 2->others */   
  24.     memset(count, 0, 3*sizeof ( int ));  
  25.       
  26.     printf("Enter a string: " );  
  27.     scanf("%s" , str);  
  28.     cal_num(str, count);  
  29.     for (i=0; i<3; i++)  
  30.     {  
  31.         switch (i)  
  32.         {  
  33.             case  0:  
  34.                 printf("num: %d/n" , count[i]);  
  35.                 break ;  
  36.             case  1:  
  37.                 printf("char: %d/n" , count[i]);  
  38.                 break ;  
  39.             case  2:  
  40.                 printf("other: %d/n" , count[i]);  
  41.                 break ;  
  42.         }  
  43.     }  
  44. }  

运行结果：

==========================================================

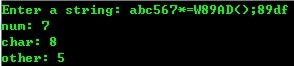
7、 数制转换（递归实现）

本算法仅实现了基数为2-16的数制转换

如果大家希望扩展范围，仅需要对基数表示字符case 进行扩展即可，如G、H、I ...

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. int  flag=1;  /* check: n/d == 0 */   
  3. void  trans_num( int  n,  int  d)  
  4. {  
  5.     int  mod;  
  6.     mod=n%d;  
  7.     n=n/d;  
  8.     while (flag && n)  
  9.         trans_num(n,d);  
  10.     flag=0;  
  11.     switch (mod)  
  12.     {  
  13.         case  10:  
  14.             printf("A" );  
  15.             break ;  
  16.         case  11:  
  17.             printf("B" );  
  18.             break ;  
  19.         case  12:  
  20.             printf("C" );  
  21.             break ;  
  22.         case  13:  
  23.             printf("D" );  
  24.             break ;  
  25.         case  14:  
  26.             printf("E" );  
  27.             break ;  
  28.         case  15:  
  29.             printf("F" );  
  30.             break ;  
  31.         default :  
  32.             printf("%d" , mod);    
  33.     }  
  34.           
  35. }  
  36. void  main()  
  37. {  
  38.     int  n, d;  
  39.     printf("Enter n d: " );  
  40.     scanf("%d %d" , &n, &d);  
  41.       
  42.     trans_num(n, d);  
  43.     printf("/n" );     
  44. }  

运行结果：

        

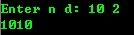
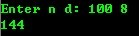
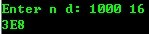
算法改进

数制直接转为字符输出，扩展支持16进制以上的数制转换

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. int  flag=1;  /* check: n/d == 0 */   
  3. void  trans_num( int  n,  int  d)  
  4. {  
  5.     int  mod;  
  6.     mod=n%d;  
  7.     n=n/d;  
  8.     while (flag && n)  
  9.         trans_num(n,d);  
  10.     flag=0;  
  11.     if (mod>=10)  
  12.         mod=mod-10+65;  /* convert to char */   
  13.     else   
  14.         mod=mod+48;  
  15.     printf("%c" , mod);   /* print char (%c) */      
  16. }  
  17. void  main()  
  18. {  
  19.     int  n, d;  
  20.     printf("Enter n d: " );  
  21.     scanf("%d %d" , &n, &d);  
  22.       
  23.     trans_num(n, d);  
  24.     printf("/n" );     
  25. }  

运行结果 （扩展进制）：

                

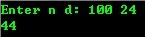
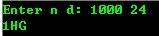
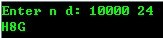
100 = 4*24+4            1000=1*24*24+17*24+16  10000=17*24*24+8*24+16        1000=27*36+28

==========================================================

8、 数制转换（栈实现）


核心思想和递归实现类似，都是压栈的原理，实现较简单，请自己尝试实现

==========================================================

9、 水仙花数

水仙花数简述： 水仙花数是指一个 n 位数 ( n≥3 )，它的每个位上的数字的 n 次幂之和等于它本身。

如：153=1 ^3+5 ^3+3 ^3（3位数）；1634=1 ^4+6 ^4+3 ^4+4 ^4（4位数）；54748=5 ^5+4 ^5+7 ^5+4 ^5+8 ^5（5位数）

判断任一3位数，是否为水仙花数

测试环境：GCC

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. main()  
  3. {  
  4.     int  b, s, g, n, sum;  
  5.     scanf("%d" , &n);  
  6.     b=n/100;  
  7.     s=n/10%10;  
  8.     g=n%10;  
  9.     sum=b*b*b+s*s*s+g*g*g;  
  10.     if (sum==n)  
  11.         printf("Yes/n" );  
  12.     else   
  13.         printf("No/n" );  
  14. }  

运行结果 （Redhat Linux）：

================================================

求4位数的水仙花数（1000<=X<=9999）

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. int  main()  
  3. {  
  4.     int  i,j,k,l,m,n;  
  5.     for (i=1; i<=9; i++)  
  6.         for (j=0; j<=9; j++)  
  7.             for (k=0; k<=9; k++)  
  8.                 for (l=0; l<=9; l++)  
  9.                     if ((i*1000+j*100+k*10+l)==i*i*i*i+j*j*j*j+k*k*k*k+l*l*l*l)  
  10.                         printf("%d%d%d%d=%d^4+%d^4+%d^4*%d^4/n" , i, j, k, l, i, j, k, l);  
  11.     return  0;  
  12. }  

运行结果：

================================================

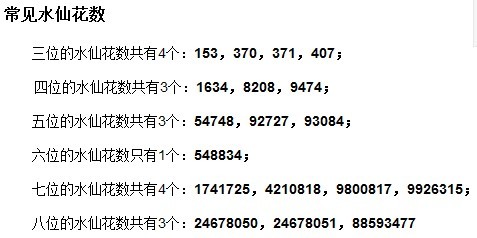
思考： 如果求得高精度大数的水仙花数，如8位、18位、28位的水仙花数（需考虑计算机精度，可采用数组或指针实现，大数计算）

==========================================================

10、 大数计算

大数运算 ：参加的值和计算结果通常是以上百位数，上千位数以及更大长度之间的整数运算，早已超出了计算机能够表示数值的精度范围（2^32=4294967296或2^64=18446744073709551616）即64位机最大也才20位，因此需要想出其它的办法计算大数。

求任意两整数之和（1000位以内）

测试环境：VC 6.0 (C)

view plain copy to clipboard print ?
·········10········20········30········40········50········60········70········80········90········100·······110·······120·······130·······140·······150
  1. #include <stdio.h>   
  2. #include <string.h>   
  3. #define MAX 1000 /* precision */   
  4. void  input( char  ch[])  
  5. {  
  6.     scanf("%s" , ch);  
  7. }  
  8. void  add( char  ch1[],  char  ch2[],  char  ch3[])  
  9. {  
  10.     int  len1, len2, len3, maxlen;  
  11.     int  sum, flag;  
  12.     len1=strlen(ch1);  
  13.     len2=strlen(ch2);  
  14.     len3=maxlen=len1 >= len2 ? len1 : len2;  
  15.     flag=0; /* jin wei */   
  16.       
  17.     while (len1>=1 && len2>=1)  
  18.     {  
  19.         sum=ch1[len1-1]-'0'  + ch2[len2-1]- '0'  + flag;  /* char -> int to calculate sum */   
  20.         flag=0;  
  21.           
  22.         if (sum>=10)  
  23.         {  
  24.             sum-=10;  
  25.             flag=1;  
  26.         }  
  27.         ch3[maxlen-1]=sum + '0' ;  
  28.         len1--;  
  29.         len2--;  
  30.         maxlen--;  
  31.     }  
  32.     while (len1>=1)  /* if num1[] is longer or maxer */   
  33.     {  
  34.         sum=ch1[len1-1]-'0'  + flag;  
  35.         flag=0;  
  36.           
  37.         if (sum>=10)  
  38.         {  
  39.             sum-=10;  
  40.             flag=1;  
  41.         }  
  42.         ch3[maxlen-1]=sum + '0' ;  
  43.         len1--;  
  44.         maxlen--;  
  45.     }  
  46.       
  47.     while (len2>=1)  /* if num2[] is longer or maxer */   
  48.     {  
  49.         sum=ch2[len2-1]-'0'  + flag;  
  50.         flag=0;  
  51.           
  52.         if (sum>=10)  
  53.         {  
  54.             sum-=10;  
  55.             flag=1;  
  56.         }  
  57.         ch3[maxlen-1]=sum + '0' ;  
  58.         len2--;  
  59.         maxlen--;  
  60.     }  
  61.     if (flag != 0)  /* if flag, then print gaowei(jinwei) */   
  62.         printf("%d" , flag);  
  63.     for ( int  i=0; i<len3; i++)   
  64.         printf("%c" , ch3[i]);     
  65.     printf("/n" );  
  66. }  
  67. int  main()  
  68. {  
  69.     char  ch1[MAX], ch2[MAX], ch3[MAX+1];  
  70.     memset(ch3, '0' ,  sizeof (ch3));  
  71.     input(ch1);  
  72.     input(ch2);  
  73.     add(ch1, ch2, ch3);  
  74.     return  0;  
  75. }  

运行结果：

   

思考： 请大家自己设计实现更复杂的大数减法、乘法、除法，求余、求幂、求最小公倍数等大数运算（提示：可用数组或链表）

==========================================================

 

 

帛逸TB
关注
专栏目录
遗传算法与深度学习实战（4）——遗传算法（Genetic Algorithm）详解与实现
盼小辉丶的博客
12-25 17万+
遗传算法（Genetic Algorithm, GA）是受自然进化原理启发的一系列搜索算法。通过模仿自然选择和繁殖的过程，遗传算法可以为涉及搜索、优化和学习的各种问题提供高质量的解决方案。同时，它们类似于自然进化，因此遗传算法可以克服传统搜索和优化算法遇到的一些障碍，尤其是对于具有大量参数和复杂数学表示形式的问题。
排序算法实现总结
qq_25626505的博客
06-27 275
一、快速排序 1） 实现一： 当将arr的第一个元素作为标准key， 需要从arr的尾端先做比较，这是因为作为标准的key，在函数partition的循环过程中一直在被移动，直到i == j的时候，key的值才固定。如果从arr首端开始比较，会出现错误； 此函数实现使用了swap函数； void swap(int* a, int* b) { int tmp = *a; *a = *b; *b = tmp; } int partition(int *arr, int i, int j) { int k
各种基本算法实现小结（五）—— 排序算法
热门推荐
阳光岛主
06-03 9万+
各种基本算法实现小结（五）—— 排序算法（均已测试通过） * 选择排序 |____简单选择排序 |____堆排序 |____归并排序* 交换排序 |____冒泡排序 |____快速排序* 插入排序 |____直接插入排序 |____折半排序 |____希尔排序* 分配排序 |____箱排序 |____基数排序=============================================
排序汇总
nihongdehuangjing的专栏
09-19 762
  各种排序方法汇总1. 基本思想：　　每一趟从待排序的数据元素中选出最小（或最大）的一个元素，顺序放在已排好序的数列的最后，直到全部待排序的数据元素排完。2. 排序过程：【示例】：   初始关键字 [49 38 65 97 76 13 27 49]第一趟排序后 13 ［38 65 97 76 49 27 49]
各种排序算法小结和实现
小胡——uYou的专栏
05-10 933
各种排序算法想必大家都不陌生，定义我就不多介绍了，直接写下自己的一些小结。快速排序：可以算的上应用最广的排序算法。其排序思路是随机选取一个数字作为标志，使得小于它的数在它左边，大于它的数在它的右边，然后递归对两边的数据排序。 归并排序：应用分之的思想，先将要排序的分为两列，然后分别进行排序，然后合并到另一 个数组中，最后再进行把它复制回来。 冒泡排序：是稳定排序，适用于排列的数组较小而且基
各种排序算法实现及总结
周大侠的专栏
08-21 665
本文主要比较一下各种排序的性能（平均时间复杂度和最差情况）和基本实现。 这个默认按照从小到大排列，输入的数据可以重复，假设输入的数组为A，下标从0到N-1注意在比较算法复杂度时，我们会关注键值的比较次数和交换次数。1、冒泡排序 冒泡排序如果不是因为名字比较好记，没有任何优势。它的思路是一趟又一趟的比较数组（或者链表也可以）中相邻的两个元素，如果前一个比后一个大，则交换。这样，每一轮之后，最大的那
各种排序算法小结
12-23
### 各种排序算法小结 #### 一、引言 排序算法是在计算机科学中非常基础且常用的一类算法。由于在实际应用中往往需要处理大量数据，因此对排序算法的效率有着较高要求。通常，我们会关注算法的时间复杂度来评估其...
PHP实现二维数组中的查找算法小结
12-19
在编程领域，数组是存储和处理数据的基本结构之一，尤其在二维数组中，常常需要执行查找算法来定位特定的元素。本文将详细讨论如何在PHP中实现几种不同的二维数组查找算法。 首先，我们来看方法1，这个算法被称为...
PHP常用排序算法实例小结【基本排序，冒泡排序，快速排序，插入排序】
10-20
1. **基本排序**（这里可能是指的选择排序）：选择排序是一种简单直观的排序算法，它的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。...
各种排序算法及其实现总结
yemers的博客
05-12 622
各种排序算法及其实现总结 排序算法总结 1.插入排序 一般来说，插入排序 都采用in-place在数组上实现。具体算法描述如下： 从第一个元素开始，该元素可以认为已经被排序 取出下一个元素，在已经排序的元素序列中从后向前扫描 如果该元素（已排序）大于新元素，将该元素移到下一位置 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置 将新元素插入到该位置中 重复步骤2 如果比较操作 的代价比交换操作 大的话，可以采用二分查找法 来减少比较操作 的数目。该算法可以认为是插入排序 的一个变种，称为二分查找排序
关于java报错问题
wei1121_的博客
12-05 144
关于java报错问题 代码会出现如下的错误，原因： 这是数组越界的错误信息，表示数组m[]的下标在遍历过程中到了n(实际上的n+1)，而在初始化时只申请了n个位置。 改进方法： 只要将数组变大一些，或者循环的次数少一些在数组范围内即可。 ...
各种排序算法的总结和实现。
学峰的学习笔记
08-22 693
最近在准备找工作，听说基本的排序算法是必考的，尤其是堆排序和快速排序。所以想自己实现一下，有些算法实现的时候，有困难，自己没能成功的实现。后来上网查到了一些前辈的博客。很不幸的是有些前辈的的博客中的排序算法是错误的。而有些虽然正确，但是算法的实现的非常的晦涩，很难看懂。所以自己总结了一下，挑选了一下，实现了一下。 现保留于此，以后有时间再来看看。
【C++】选择排序递归实现
weixin_54695073的博客
03-20 2199
蓝桥杯——递归实现选择排序
C语言项目实战知识点汇总
SingWeek
06-30 1870
C语言项目实战知识点汇总常用头文件宏定义函数声明局部变量和全局变量输入输出判断语句if、switch循环语句while、for函数的定义按键监听、随机数指针数组操作时间戳、日期转换待补充 运行环境：Dev-C++ 6.5 常用头文件 #include<stdio.h> //标准输入输出函数库（printf、scanf） #include<time.h> //用于获得随机数 #include<windows.h> //控制dos界面 #include
排序算法总结
yizhiniu_xuyw的专栏
11-15 2252
前言 查找和排序算法是算法的入门知识，其经典思想可以用于很多算法当中。因为其实现代码较短，应用较常见。所以在面试中经常会问到排序算法及其相关的问题。但万变不离其宗，只要熟悉了思想，灵活运用也不是难事。 一般在面试中最常考的是快速排序和归并排序，并且经常有面试官要求现场写出这两种排序的代码。对这两种排序的代码一定要信手拈来才行。还有插入排序、冒泡排序、堆排序、基数排序、桶排序等。面试官对于这些排序可能会要求比较各自的优劣、各种算法的思想及其使用场景。还有要会分析算法的时间和空间复杂度。通常查找和排序算法的
算法设计与分析（第二版）上机实验题——C语言实现
qq_44839044的博客
03-10 1万+
算法设计与分析第一章实验1.统计求最大、最小元素的平均比较次数实验2.求无序序列中第k小的元素 第一章 实验1.统计求最大、最小元素的平均比较次数 代码如下： #include <stdio.h> #include <stdlib.h> #include <time.h> int main() { int a[10],i,b,c,d=0,e,f; srand((unsigned)time(NULL)); printf("有下列数字："); for
复试机试 -- C语言习题
追風少年
04-23 3433
01 求第二大数 题目描述： 写一个函数找出一个整数数组中，第二大的数 代码： #include <stdio.h> #define N 105 int secondMax(int a[],int n){ int Max=a[0],s_Max=-32767; int i; for(i=1;i<n;i++){ if(a[i]>Max){ s_Max=Max;...
[代码实例][C]Linux多线程编程示例
火云的专栏
11-14 161
#include <stdio.h> #include <stdlib.h> #include <time.h> #include <stdbool.h> #include <stdint.h> #include <pthread.h> typedef struct { int * array_num; int count; bool is_front; } thread_arg; #define NUM_COUNT 10
MATLAB实现小波提升算法的关键步骤解析
本文主要介绍了小波提升算法的基本概念、MATLAB实现小波提升算法的步骤和要点以及该算法在实际应用中的效果。小波提升算法由于其良好的性能，在许多信号处理领域有着广泛的应用前景。在MATLAB环境下，借助其强大的...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值