LeetCode 005. Longest Palindromic Substring

Longest Palindromic Substring

 

Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.

求最长回文字符串，最直观的做法是分别检测字符串S的所有子字符串是否为回文字符串。长度为n的字符串S，其子字符串的总数目为n+(n-1)+……+3+2+1 = n*(n+1)/2

判断子字符串是否为回文字符串算法复杂度O(n)就可以实现，因此总的来说此算法复杂度为O(n^3)。

这种直观的算法复杂度很高，在此就不采用了。这种直观的算法思路很明了，就是从外向里去检测的，而回文字符串左右对称，必定有一个对称点。我们如果能将这个对称点找出，然后再左右扩展，是不是就可以找出最长的回文子字符串了呢？

举个例子来说吧，S=“abcdeedcba”这个字符串是回文字符串，当我们循环到ee处时，我们发现我们找到一个对称点了，我们就可以左右扩展：判断ee左右各添加一个字符，是否仍是回文字符串，如此循环下去。

这个时候有可能会有这种字符串 S=“abcdefedcba”，这个字符串也是回文字符串的，对称点是 f 字符。既然有这种情况，我们就得将每一个字符都当做对称点然后左右扩展了。

总体来说，这是有两种情况的，我们需要分别对待，分别考虑。主要分两种假设来分别考虑：（1）、回文字符串长度为偶数；（2）、回文字符串长度为奇数。之后再将两者的最长挑出来。这种算法的复杂度为O(n^2)

class Solution 
{
public:
    string longestPalindrome(string s) 
	{
		int len = s.length();
		string palindorme;
		int maxlen = 0;
		int templen = 0;
		int i,j;
		//回文字符串长度为偶数
		for(i=0; i<len-1; i++)
		{
			if(s[i]==s[i+1])
			{
				j = 1;
				while(i-j>=0 && i+j+1<len && s[i-j]==s[i+j+1])
					++j;
				if(2*j > maxlen)
				{
					maxlen = 2*j;
					palindorme = s.substr(i-j+1,maxlen);
				}
			}
		}

		//回文字符串长度为奇数
		for(i=0; i<len; i++)
		{
			j = 0;
			while(i-j>=0 && i+j<=len-1 && s[i-j]==s[i+j])
				++j;
			templen = 2*j-1;
			if(templen > maxlen)
			{
				maxlen = templen;
				palindorme = s.substr(i-j+1,maxlen);
			}
		}
		return palindorme;
    }
};

经过搜索后，发现这种算法还并非是最优算法，还有一种复杂度为O(n)的算法—— manacher算法

http://blog.csdn.net/xingyeyongheng/article/details/9310555 这篇博客介绍manacher算法逻辑比较清晰，下面就以该博客为主体，对其做些许修改。

算法介绍如下：

定义数组 p[i] 表示以i为中心的(包含 i 这个字符)回文字符串半径长度

将字符串s从前扫到后 for(int i=0; i<s.length(); i++) 来计算 p[i]，则最大的p[i]就是最长回文串长度，则问题是如何去求 p[i] ？

由于s是从前扫到后的,所以需要计算p[i]时一定已经计算好了p[1]……p[i-1]

假设现在扫描到了i+k这个位置,现在需要计算p[i+k]

定义 maxlen 是 i+k 位置前所有回文串中能延伸到的最右端的位置，即 maxlen=p[i]+i; //p[i]+i 表示最大的。

共有三种情况需要讨论：（下面图中黑色是 i 的回文字符串范围，蓝色是 i-k 的回文字符串范围）

第一种情况：i+k这个位置不在前面的任何回文串中，即 i+k>maxlen，则初始化p[i+k]=1;//本身是回文串

然后 p[i+k] 左右延伸，即 while(s[i+k+p[i+k]] == s[i+k-p[i+k]]) ++p[i+k]

为了防止越界我们加上边界判断条件while(i+k+p[i+k]<len && i+k-p[i+k]>=0 && s[i+k+p[i+k]] == s[i+k-p[i+k]])++p[i+k];

很多博客都用字符串左右添加特殊符号*或者@的方式，这里不采用这种方法，而是直接加上边界条件判断。

第一种情况图示：

或者，如下情况

第二种情况：i+k这个位置刚好被前面以位置i为中心的回文串包含，即maxlen>i+k，这种情况与情况一是相同的，还是需要重新判断 i+k 的回文字符串长度。

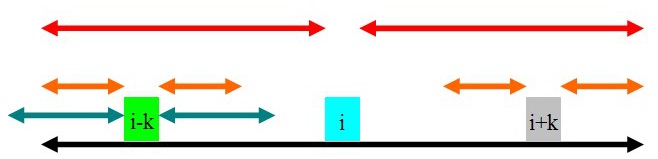
第三种情况：i+k这个位置被前面以位置i为中心的回文串包含，即maxlen>i+k，这样的话 p[i+k] 就不是从1开始。由于回文串的性质，可知i+k这个位置关于i与i-k对称。

i-k回文字符串范围有一部分在 i 的回文字符串之外，如下图靛色左端在黑色左端之外。

这种情况 p[i+k] = p[i]-k ; //maxlen-(i+k)=p[i]-k，即半径为橙色部分

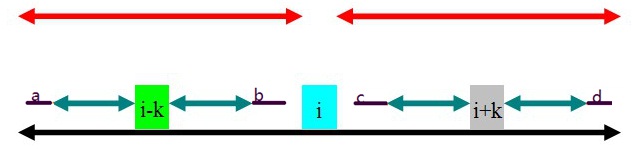
那么p[i+k]有没有可能更长呢？答案是不可能的。证明如下：

如上图，假设p[i+k]可以延长，增加紫色部分，我们将左右分别称为c和d，由i+k的回文字符串特性可知c=d，

根据 i 的回文字符串特性，我们可以知道与c对应的应该会有b，c=b

再根据i-k的回文字符串特性b和紫色部分a对称，最终得到a=b

总结上述a=b=c=d，则 i 的回文字符串长度就不会仅仅是黑色长度了，而是黑色+左右两端紫色部分了，这与已经求出的 i 的回文字符串长度仅为黑色长度矛盾，所以假设不成立，则 p[i+k]=p[i]-k; //maxlen-(i+k)

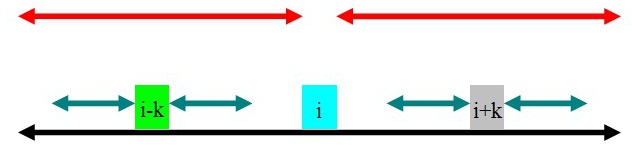
第四种情况：i+k这个位置被前面以位置i为中心的回文串包含，即maxlen>i+k，这样的话 p[i+k] 就不是从1开始。由于回文串的性质，可知i+k这个位置关于i与i-k对称。

i-k 回文字符串全部落在 i 的回文字符串内，如下图，此时p[i+k] = p[i-k]。

p[i+k]还有没有可能更长呢？我们仍然采用反证法来证明

假设p[i+k]可以延长并增加紫色部分c和d，c=d

由 i 的回文字符串对称特性，a=d ，b=c，又c=d 故a=b

这与前面已经计算出 i-k 的回文字符串长度仅为靛色长度矛盾，故假设不成立。

将上面四种情况综合在一起就是：

p[i+k] = min(p[i-k], p[i]-k); //k=(i+k)-i

while(i+k+p[i+k]<len && i+k-p[i+k]>=0 && s[i+k+p[i+k]] == s[i+k-p[i+k]])++p[i+k];

根据上面的算法我们知道p[i] 是以 i 为中心的回文字符串长度，那么对于aa这种偶数长度的回文字符串，其对称中心 i 并不是一个字符，如何将偶数长度的回文字符串和奇数长度的回文字符串统一起来呢？manacher算法提供了一个非常巧妙的思路，那就是将字符串所有字符左右都插入一个 '#' 字符。如 aba 则变成 #a#b#a#，aa 则变成#a#a#，如此一来回文字符串中心均为一个字符，而不会为空！

下面来看下代码：

class Solution 
{
public:
	string preprocess(string s) //将字符串中插入'#'字符
	{
		int len = s.length();
		string str(2*len+1, '#');
		for(int i=0; i<len; i++)
			str[2*i+1] = s[i];
		return str;
	}

	string longestPalindrome(string s) 
	{
		string str = preprocess(s);
		string palindrome;
		int len = str.length();
		int i,id = 0;
		int maxlen = 0; //回文字符串最长半径
		int index = 0;  //回文字符串中心下标
		int * p = new int[len];	
		p[0] = 0;
		for(i=0; i<len; i++)
		{
			if(p[i]+id>i)
				p[i]=min(p[2*id-i], p[id]+id-i);
			else 
				p[i]=1;
			while(i-p[i]>=0 && i+p[i]<len && str[i-p[i]]==str[i+p[i]])
				++p[i];
			if(id+p[id] < i+p[i])
				id = i;
			if(maxlen<p[i])
			{
				maxlen = p[i];	
				index = i;
			}
		}
		delete[] p;
		palindrome = s.substr((index-maxlen+1)/2,maxlen-1);
		return palindrome;
	}
};