LeetCode 004. Median of Two Sorted Arrays

于 2014-05-07 19:04:00 发布
阅读量1.2k 收藏
点赞数
分类专栏： Leetcode LeetCode - C++
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/wanghuiqi2008/article/details/25239831
版权

Median of Two Sorted Arrays

 

There are two sorted arrays A and B of size m and n respectively. Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).



这道题一开始是想用如下方法做的：

/********************************************************************************************************************************************************************************

2个有序数组求合并后的中位数

第一步：假设两个有序数组（已经各自排序完成了）长度相等，试写函数找出两个数组合并后的中位数。 第二步：假设两个有序数组长度不等，一样的求出中位数

解析： 这个题目看起来非常简单。第一题的话： 假设数组长度为n, 那么我就把数组1和数组2直接合并，然后再直接找到中间元素。对于这样的方案，第一题和第一题就没有什么区别了。这样的话时间复杂度就是O(n)。通常在这样的情况下，那些mentor类型的达人就会循循善诱道：“你还有更好的办法吗:)” 如果比线性更高效，直接能想到的就是对数了O(log(n)),这个时间复杂度在这里可能吗？ 当然还是可能的。来继续看看下面的分析。

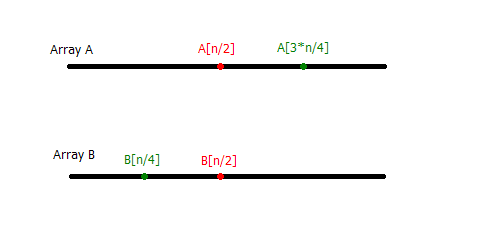
先找来了一个图(自己画的，简陋了点)

sample

我们先来分析看看： 想到对数的效率，首先想到的就是二分查找，对于这个题目二分查找的意义在哪里呢？

我们找到了A[n/2] 和 B[n/2]来比较，

如果他们相等，那样的话，我们的搜索结束了，因为答案已经找到了A[n/2]就肯定是排序后的中位数了。

如果我们发现B[n/2]>A[n/2]，说明什么,这个数字应该在 A[n/2]->A[n]这个序列里面， 或者在 B[1]-B[n/4]这里面。 或者，这里的或者是很重要的， 我们可以说，我们已经成功的把问题变成了在排序完成的数组A[n/2]-A[n]和B[0]-B[n/2]里面找到合并以后的中位数， 显然递归是个不错的选择了。

类似的， 如果B[n/2]<A[n/2]呢？显然就是在A[0]-A[n/2]和B[n/2]-B[n]里面寻找了。

在继续想， 这个递归什么时候收敛呢？当然一个case就是相等的值出现， 如果不出现等到这个n==1的时候也就结束了。

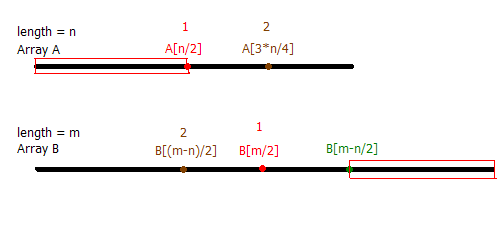
马上有人说那不定长的怎么办呢？一样的，我们还是来画个图看看：(我的画图水平肯定提高了)

sample2

一样的， 我们还是把这个两个数组来比较一下，不失一般性，我们假定B数组比A数组长一点。A的长度为n, B的长度为m。比较A[n/2]和B[m/2] 时候。类似的，我们还是分成几种情况来讨论：

a. 如果A[n/2] == B[m/2]，那么很显然，我们的讨论结束了。A[n/2]就已经是中位数，这个和他们各自的长度是奇数或者偶数无关。

b. 如果A[n/2] <   B[m/2]，那么，我们可以知道这个中位数肯定不在[A[0],A[n/2])这个区间内，同时也不在[B[m/2],B[m]]这个区间里面。这个时候，我们不能冲动地把[A[0],A[n/2])和[B[m/2],B[m]]全部扔掉。我们只需要把[B[m-n/2],B[m]]和[A[0],A[n/2])扔掉就可以了。（如图所示的红色线框），这样我们就把我们的问题成功转换成了如何在A[n/2]->A[n]这个长度为n/2的数组和B[1]-B[m-n/2]这个长度为m-n/2的数组里面找中位数了。问题复杂度即可下降了。

c. 只剩下A[n/2] > B[m/2]，和b类似的，我们可以把A[n/2]->A[n]这块以及B[1]->B[n/2]这块扔掉了就行,然后继续递归。

********************************************************************************************************************************************************************************/

按照作者的这种思路，每次都能删掉数组的一半元素。按照这种思想去实现代码，实现到最后就会有个问题：m==1或者n==1的边界问题。

当m==1或者n==1时，每次的衰减因子decrease = (m/2 < n/2)? m/2 : n/2; 此时就等于0了，等于0的话那递归循环去找中位数是没有效果的，可以认为是一个死循环。因此m==1或者n==1必须要为他设定一个退出循环的条件！我们来看下面的两个例子（为了方便说明，我们将B数组下标与值设定是相同的）：

例1、B数组有偶数个元素，则中位数必定为一个数，而不是两个数的平均值

A[]={x};                                   // x为任意值

B1[]={0,1,2,3,4,5,6,7,8,9};    // B1数组有偶数个元素

（1）A[0]>=B[10/2]                 那么中位数必定是B[10/2] = 6

（2）A[0]<=B[10/2-1]              那么中位数也必定是B[10/2-1]=5

（3）B[10/2-1]<A[0]<B[10/2]   那么中位数是A[0]

这个是有确定结果的。

例2、B有奇数个元素，则中位数必定是两个数值的平均值

A[]={x};                                   // x为任意值

B1[]={0,1,2,3,4,5,6,7,8};        // B1数组有奇数个元素


情况有些多，我们再来一一分析一下

（1）A[0]<=B[9/2-1]                  则中位数为(B[9/2-1]+B[9/2])/2    （上图蓝色框部分）

（2）B[9/2-1]<A[0]<B[9/2+1]     则中位数为(A[0]+B[9/2])/2          （上图黄色框部分）

（3）B[9/2+1]<=A[0]                 则中位数为(B[9/2]+B[9/2+1])/2    （上图绿色框部分）

按照这种思路实现出来的代码如下：

class Solution {
public:

    double findMedianSortedArrays(int A[], int m, int B[], int n) 
	{
		double mida,midb;   //A、B两数组的中位数
		int decrease;

		if(m==0)      
		{
			if(n%2==0) 
				//注意：static_cast<double>((B[n/2-1]+B[n/2])/2)这么写是将除法运算后的结果转成double类型，但除法是按照整形来做的
				//因此static_cast<double>((B[n/2-1]+B[n/2])/2) = static_cast<double>((2+3)/2)=static_cast<double>(5/2)=static_cast<double>(2)=2.0
				return static_cast<double>(B[n/2-1]+B[n/2])/2;  
			else 
				return B[n/2];		
		}
		if(n==0)
		{
			if(m%2==0) 
				return static_cast<double>(A[m/2-1]+A[m/2])/2;
			else
				return A[m/2];			
		}

		if (m==1 && n==1)
			return static_cast<double>(A[0]+B[0])/2;

		if(m==1)
		{
			if(n%2==0)
			{
				if(A[0]>=B[n/2])
					return B[n/2];
				else if(A[0]<=B[n/2-1])
					return B[n/2-1];
				else if(A[0]<B[n/2] && A[0]>B[n/2-1])
					return A[0];
			}
			else
			{
				if(A[0]<=B[n/2-1])
					return static_cast<double>(B[n/2-1]+B[n/2])/2;
				else if(A[0]>B[n/2-1] && A[0]<B[n/2+1])
					return static_cast<double>(B[n/2]+A[0])/2;
				else if(A[0]>=B[n/2+1])
					return static_cast<double>(B[n/2]+B[n/2+1])/2;			
			}				

		}
		if(n==1)
		{
			if(m%2==0)
			{
				if(B[0]>=A[m/2])
					return A[m/2];
				else if(B[0]<=A[m/2-1])
					return A[m/2-1];
				else if(B[0]<A[m/2] && B[0]>A[m/2-1])
					return B[0];
			}
			else
			{
				if(B[0]<=A[m/2-1])
					return static_cast<double>(A[m/2-1]+A[m/2])/2;
				else if(B[0]>A[m/2-1] && B[0]<A[m/2+1])
					return static_cast<double>(A[m/2]+B[0])/2;
				else if(B[0]>=A[m/2+1])
					return static_cast<double>(A[m/2]+A[m/2+1])/2;			
			}	
		
		}


        if(m%2==0) 
			mida = static_cast<double>((A[m/2-1]+A[m/2]))/2;    //此类情况下m必定是大于等于2的
		else
			mida = A[m/2];
		if(n%2==0) 
			midb = static_cast<double>((B[n/2-1]+B[n/2]))/2;
		else 
			midb = B[n/2];
		
		decrease = (m/2 < n/2)? m/2 : n/2;

		if(mida == midb)
			return mida;
		else if(mida < midb)  //中位数在A的右半部分+B的左半部分
		{
			return findMedianSortedArrays(&A[decrease], m-decrease, &B[0], n-decrease);
		}
		else if(mida > midb)  //中位数在B的右半部分+A的左半部分
		{			
			return findMedianSortedArrays(&A[0], m-decrease, &B[decrease], n-decrease);
		}

    }


};

但是这是有天然的缺陷啊！ 大哭 大哭 大哭

测试用例

A[]={1,2,6}

B[]={3,4,5}

然后程序运行结果是3.0000，很明显不正确啊

分析可知当m+n是偶数，则中位数是两个数的平均值，这时候上面的思路及程序只适用于这两个数一个在A数组一个在B数组的情况，并不能满足这两个数同时位于一个数组中的情况（如本测试用例）！

这种缺陷应该是可以弥补的，等大牛来解！


***************************************************************************************************************************************************************************************

***************************************************************************************************************************************************************************************

下面介绍另外一种思路（未完待续……）

这种思路的参考博客链接如下：

1、点击打开链接   2、点击打开链接      3、点击打开链接

这三篇博客用的都是同一种思路，第一篇用英文介绍了下面要列的思路，第二篇博客对英文进行了翻译，并进行了详细的解释。第三篇博客也是这个思路，就不多说了。


方案1：假设两个数组总共有n个元素，那么显然我们有用O(n)时间和O(n)空间的方法：用merge sort的思路排序，排序好的数组取出下标为k-1的元素就是我们需要的答案。
这个方法比较容易想到，但是有没有更好的方法呢？
方案2：我们可以发现，现在我们是不需要“排序”这么复杂的操作的，因为我们仅仅需要第k大的元素。我们可以用一个计数器，记录当前已经找到第m大的元素了。同时我们使用两个指针pA和pB，分别指向A和B数组的第一个元素。使用类似于merge sort的原理，如果数组A当前元素小，那么pA++，同时m++。如果数组B当前元素小，那么pB++，同时m++。最终当m等于k的时候，就得到了我们的答案——O(k)时间，O(1)空间。
但是，当k很接近于n的时候，这个方法还是很费时间的。当然，我们可以判断一下，如果k比n/2大的话，我们可以从最大的元素开始找。但是如果我们要找所有元素的中位数呢？时间还是O(n/2)=O(n)的。有没有更好的方案呢？
我们可以考虑从k入手。如果我们每次都能够剔除一个一定在第k大元素之前的元素，那么我们需要进行k次。但是如果每次我们都剔除一半呢？所以用这种类似于二分的思想，我们可以这样考虑：

Assume that the number of elements in A and B are both larger than k/2, and if we compare the k/2-th smallest element in A(i.e. A[k/2-1]) and the k-th smallest element in B(i.e. B[k/2 - 1]), there are three results:
(Becasue k can be odd or even number, so we assume k is even number here for simplicy. The following is also true when k is an odd number.)
A[k/2-1] = B[k/2-1]
A[k/2-1] > B[k/2-1]
A[k/2-1] < B[k/2-1]
if A[k/2-1] < B[k/2-1], that means all the elements from A[0] to A[k/2-1](i.e. the k/2 smallest elements in A) are in the range of k smallest elements in the union of A and B. Or, in the other word, A[k/2 - 1] can never be larger than the k-th smalleset element in the union of A and B.

Why?
We can use a proof by contradiction. Since A[k/2 - 1] is larger than the k-th smallest element in the union of A and B, then we assume it is the (k+1)-th smallest one. Since it is smaller than B[k/2 - 1], then B[k/2 - 1] should be at least the (k+2)-th smallest one. So there are at most (k/2-1) elements smaller than A[k/2-1] in A, and at most (k/2 - 1) elements smaller than A[k/2-1] in B.So the total number is k/2+k/2-2, which, no matter when k is odd or even, is surly smaller than k(since A[k/2-1] is the (k+1)-th smallest element). So A[k/2-1] can never larger than the k-th smallest element in the union of A and B if A[k/2-1]<B[k/2-1];
Since there is such an important conclusion, we can safely drop the first k/2 element in A, which are definitaly smaller than k-th element in the union of A and B. This is also true for the A[k/2-1] > B[k/2-1] condition, which we should drop the elements in B.
When A[k/2-1] = B[k/2-1], then we have found the k-th smallest element, that is the equal element, we can call it m. There are each (k/2-1) numbers smaller than m in A and B, so m must be the k-th smallest number. So we can call a function recursively, when A[k/2-1] < B[k/2-1], we drop the elements in A, else we drop the elements in B.


We should also consider the edge case, that is, when should we stop?
1. When A or B is empty, we return B[k-1]( or A[k-1]), respectively;
2. When k is 1(when A and B are both not empty), we return the smaller one of A[0] and B[0]
3. When A[k/2-1] = B[k/2-1], we should return one of them

In the code, we check if m is larger than n to garentee that the we always know the smaller array, for coding simplicy.

翻译如下：

首先假设数组A和B的元素个数都大于k/2，我们比较A[k/2-1]和B[k/2-1]两个元素，这两个元素分别表示A的第k/2小的元素和B的第k/2小的元素。这两个元素比较共有三种情况：>、<和=。如果A[k/2-1]<B[k/2-1]，这表示A[0]到A[k/2-1]的元素都在A和B合并之后的前k小的元素中。换句话说，A[k/2-1]不可能大于两数组合并之后的第k小值，所以我们可以将其抛弃。

证明也很简单，可以采用反证法。假设A[k/2-1]大于合并之后的第k小值，我们不妨假定其为第（k+1）小值。由于A[k/2-1]小于B[k/2-1]，所以B[k/2-1]至少是第（k+2）小值。但实际上，在A中至多存在k/2-1个元素小于A[k/2-1]，B中也至多存在k/2-1个元素小于A[k/2-1]，所以小于A[k/2-1]的元素个数至多有k/2+ k/2-2，小于k，这与A[k/2-1]是第（k+1）的数矛盾。

当A[k/2-1]>B[k/2-1]时存在类似的结论。

当A[k/2-1]=B[k/2-1]时，我们已经找到了第k小的数，也即这个相等的元素，我们将其记为m。由于在A和B中分别有k/2-1个元素小于m，所以m即是第k小的数。(这里可能有人会有疑问，如果k为奇数，则m不是中位数。这里是进行了理想化考虑，在实际代码中略有不同，是先求k/2，然后利用k-k/2获得另一个数。)

通过上面的分析，我们即可以采用递归的方式实现寻找第k小的数。此外我们还需要考虑几个边界条件：

  • 如果A或者B为空，则直接返回B[k-1]或者A[k-1]；
  • 如果k为1，我们只需要返回A[0]和B[0]中的较小值；
  • 如果A[k/2-1]=B[k/2-1]，返回其中一个；
实现代码如下： 

double findKth(int a[], int m, int b[], int n, int k)
{
	//always assume that m is equal or smaller than n
	if (m > n)
		return findKth(b, n, a, m, k);
	if (m == 0)
		return b[k - 1];
	if (k == 1)
		return min(a[0], b[0]);
	//divide k into two parts
	int pa = min(k / 2, m), pb = k - pa;
	if (a[pa - 1] < b[pb - 1])
		return findKth(a + pa, m - pa, b, n, k - pa);
	else if (a[pa - 1] > b[pb - 1])
		return findKth(a, m, b + pb, n - pb, k - pb);
	else
		return a[pa - 1];
}

class Solution
{
public:
	double findMedianSortedArrays(int A[], int m, int B[], int n)
	{
		int total = m + n;
		if (total & 0x1)
			return findKth(A, m, B, n, total / 2 + 1);
		else
			return (findKth(A, m, B, n, total / 2) + findKth(A, m, B, n, total / 2 + 1)) / 2;
	}
};

这段代码运行结果是Accept的，我们来看一下他是如何避免上面思路出现的问题的。

测试序列为：

A[]={1,2,6}

B[]={3,4,5}

在运行过程中我们发现每次他只删除一个数组的一半，而不是像上思路中那样，同时删除两个数组相同数量的元素。








雪水
关注
专栏目录
LeetCode4 Median of Two Sorted Arrays
01-09
There are two sorted arrays nums1 and nums2 of size m and n respectively. ...Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)). Java AC版本
leetcode无法登录-MedianOfTwoSortedArrays:双排序数组的中位数
07-01
leetcode 无法登录两个有序数组的中位数 问题 有两个大小分别为 m 和 n 的排序数组 nums1 和 nums2。求两个排序数组的中位数。 整体运行时间复杂度应该是 O(log (m+n))。 您可以假设 nums1 和 nums2 不能都为空。 ...
java-leetcode题解之004-Median-of-Two-Sorted-Arrays
最新发布
08-31
java入门 java_leetcode题解之004_Median_of_Two_Sorted_Arrays
LeetCodeTest.zip
06-14
"Median of Two Sorted Arrays"可能涉及到二分查找和数组合并；"Longest Palindromic Substring"可能涉及到动态规划或者Manacher's Algorithm。这些题目不仅锻炼了我们的编程技巧，还让我们对算法有了更深入的理解。...
leetcode4median-leetcode4-median-:leetcode4-中位数-
07-06
在LeetCode上，题目4（Median of Two Sorted Arrays）是一个经典的算法问题，旨在寻找两个已排序数组的中位数。中位数是将一组数值从小到大排列后处于中间位置的数，在奇数个数的情况下是中间的那个数，而在偶数个数...
leetcodepython001-leetcode:https://leetcode.com/的解决方案
07-01
Arrays.cpp │  │  └── 005 - Longest Palindromic Substring.cpp │  └── python │  ├── 001 - Two Sum.py │  ├── 002 - Add Two Numbers.py │  ├── 003 - Longest Substring Without ...
Java-LeetCode算法题解析.pdf
07-15
#### 四、Median of Two Sorted Arrays（两个有序数组的中位数） **问题描述：** 给定两个大小分别为 `m` 和 `n` 的正序数组 `nums1` 和 `nums2`。请找出并返回这两个正序数组的中位数。 **解析：** 此问题可以...
lrucacheleetcode-LeetCodeSheet:记录自己Leetcode之旅
06-29
Median of Two Sorted Arrays 注意：后两题是与快速排序非常相似的快速选择（Quick Select）算法，面试中很常考 链表类（Linked List）： 基础知识：链表如何实现，如何遍历链表。链表可以保证头部尾部插入删除操作...
程序员面试宝典LeetCode刷题手册
05-18
4. Median of Two Sorted Arrays 7. Reverse Integer 9. Palindrome Number 11. Container With Most Water 13. Roman to Integer 15. 3Sum 16. 3Sum Closest 17. Letter Combinations of a Phone Number 18. 4Sum ...
_leetcode-python.pdf
06-18
文档内容目录显示了一系列问题编号和对应的题目，例如“Two Sum”，“Add Two Numbers”，“Median of Two Sorted Arrays”等，这些都是典型的算法和数据结构问题。这些问题涵盖了数组操作、字符串处理、递归、动态...
leetcode知乎-leetcode:leetcode解决方案
06-30
leetcode 知乎 此项目介绍 此项目旨在是为leetcode里面的习题提供解析（数据结构相关知识），锻炼了自己，同时也给别人带来了方便。 网站习题链接： ** 作者知乎链接**： 关于习题 所有习题和解析都写在一个文件里，...
leetcode-master.zip
07-09
4. "004_median_of_two_sorted_arrays"：这个题目是“寻找两个有序数组的中位数”。需要在两个已排序的数组中找到中位数，如果两个数组合并后的数组有偶数个元素，中位数就是中间两个数的平均值。这个问题通常用二分...
LeetCode题解（java语言实现）.pdf
04-22
* Median of Two Sorted Arrays Java：该题目要求找到两个排序数组的中位数，实现方法使用了二分查找算法。 * Regular Expression Matching in Java：该题目要求匹配字符串和正则表达式，实现方法使用了动态规划算法...
lrucacheleetcode-leetcode-1:leetcode-1
06-29
Median of Two Sorted Arrays 求两有序数列的中位数，可泛化为求两有序数列的第k位数，二分法 5. Longest Palindromic Substring 最长回文子串，补符号，记忆 6. ZigZag Conversion 观察规律 7. Reverse Integer ...
lrucacheleetcode-leetcode:leetcode
06-29
lru缓存leetcode leetcode 1. Two Sum 2. Add Two Numbers 3. Longest Substring Without Repeating Characters 4. Median of Two Sorted Arrays 5. Longest Palindromic Substring 7. Reverse Integer 9. ...
LeetCode题解 - Java语言实现-181页.pdf
06-04
7. Median of Two Sorted Arrays in Java 两个排序数组的中位数是一个经典的数组问题，要求找到两个排序数组的中位数。可以使用归并排序或二分搜索来解决该问题。 8. Regular Expression Matching in Java 正则...
LeetCode题目集1
08-08
4. **Median of Two Sorted Arrays** (Hard) 这是一道查找两个已排序数组中中位数的题目。要求整体时间复杂度为O(log (m+n))。可以采用二分查找的方法，不断缩小查找范围，找到两个数组合并后中间位置的元素，或者...
LeetCode 刷题汇总1
08-03
* 两个排序数组的中位数（Median of Two Sorted Arrays）：计算两个排序数组的中位数。 * 整数到罗马（Integer to Roman）：将整数转换为罗马数字。 * 罗马到整数（Roman to Integer）：将罗马数字转换为整数。 4...
给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 算法的时间复杂度应该为 O(log (m+n)) 。 来源：力扣（LeetCode） 链接：https://leetcode.cn/problems/median-of-two-sorted-arrays 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
06-10
可以使用二分查找算法来解决这个问题。 首先，我们可以将两个数组合并成一个有序数组，然后求出中位数。但是，这个方法的时间复杂度为 $O(m + n)$，不符合题目要求。因此，我们需要寻找一种更快的方法。...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值