LeetCode题解-104-Maximum Depth of Binary Tree

尽管写LeetCode解答主要是为了自己整理思路，但是如果对您也正好有帮助，请点个赞给菜鸟一点鼓励吧 :-)

原题

解法分析

解法1使用递归法；

解法2参考了别人的思路，为迭代法，类似于广度优先搜索；

自己的迭代法使用了后序遍历来统计树的深度，较为繁琐，没有参考意义。

解法1

解法分析

递归计算左子树的深度与右子树的深度，那么树的深度为两个子树中深度的较大值+1。

代码

public class Solution104_iterator {
    public int maxDepth(TreeNode root) {
        if (root == null)
            return 0;

        Deque<TreeNode> stack = new LinkedList<TreeNode>();

        stack.push(root);
        int count = 0;

        while (!stack.isEmpty()) {
            int size = stack.size();
            while (size-- > 0) {
                TreeNode cur = stack.pop();
                if (cur.left != null)
                    stack.addLast(cur.left);
                if (cur.right != null)
                    stack.addLast(cur.right);
            }
            count++;

        }
        return count;
    }
}

解法2

参考了https://discuss.leetcode.com/topic/4087/simple-solution-using-java/4

解法分析

类似于广度优先搜索，使用一个队列。队列初始为空，每次都会加入第i层的所有节点，如果队列不为空，说明该层有节点，因此count++；同时，删除第i层所有的节点，加入第i+1层的所有节点，继续进行判断。如果队列为空，说明树已经到底，结束。、

图解

以下图所示的树为例，深度为3层。

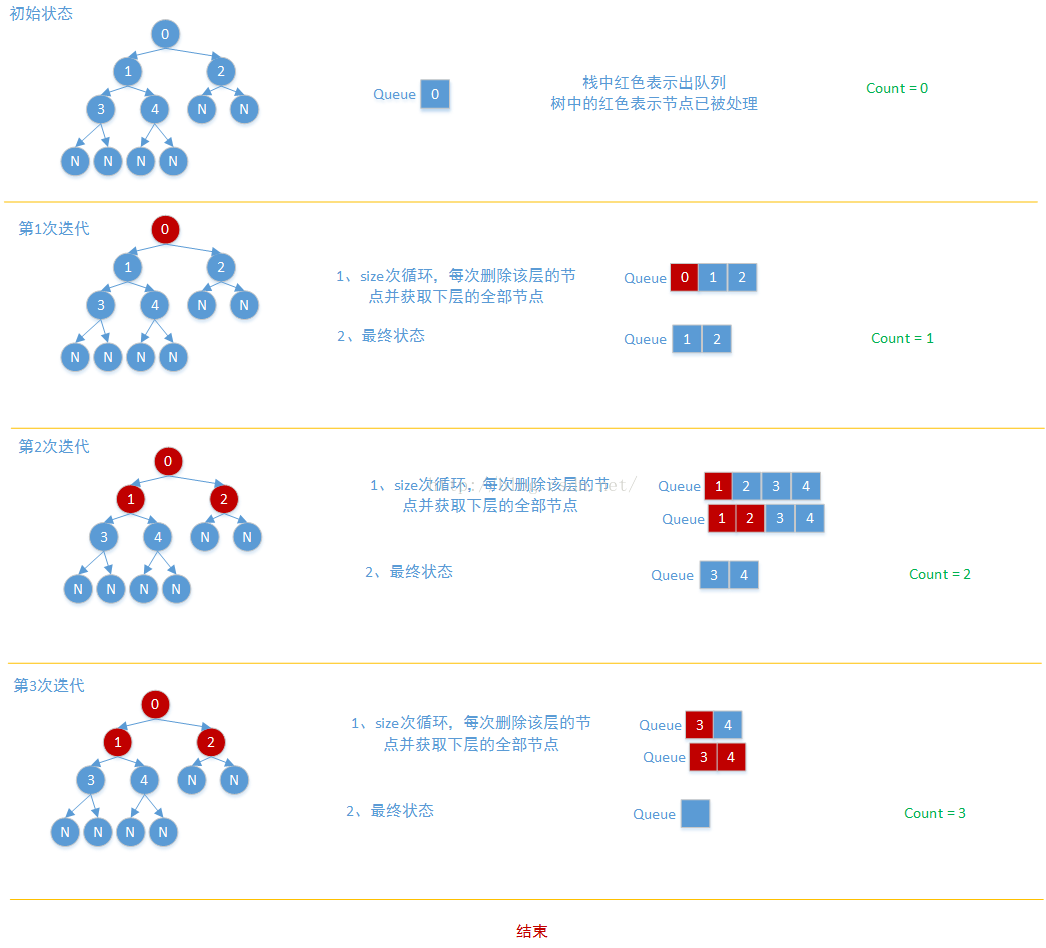
代码

public class Solution104_iterator {
    public int maxDepth(TreeNode root) {
        if (root == null)
            return 0;

        Deque<TreeNode> stack = new LinkedList<TreeNode>();

        stack.push(root);
        int count = 0;

        while (!stack.isEmpty()) {
            int size = stack.size();
            while (size-- > 0) {
                TreeNode cur = stack.pop();
                if (cur.left != null)
                    stack.addLast(cur.left);
                if (cur.right != null)
                    stack.addLast(cur.right);
            }
            count++;

        }
        return count;
    }
}