Legendre's three-square theorem

最新推荐文章于 2019-07-20 12:30:17 发布

MichaelWen_

最新推荐文章于 2019-07-20 12:30:17 发布

阅读量1k

点赞数

文章标签：维基百科

本文介绍了数学中Legendre的三平方定理，该定理阐述了一个自然数能被表示为三个整数平方和的条件，并列举了不能如此表示的最小自然数序列。文中回顾了该定理的历史发展，包括Fermat、Legendre、Cauchy等人的贡献。

摘要由CSDN通过智能技术生成

From Wikipedia, the free encyclopedia

In mathematics, Legendre's three-square theorem states that a natural number can be represented as the sum of three squares of integers

n = x^2 + y^2 + z^2

if and only if $n$ is not of the form 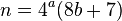$n = 4^a(8b + 7)$ for integers $a$ and $b$ .

The first numbers that cannot be expressed as the sum of three squares (i.e. numbers that can be expressed as 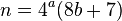$n = 4^a(8b + 7)$ ) are

7, 15, 23, 28, 31, 39, 47, 55, 60, 63, 71 ... (sequence A004215 in OEIS).

[hide]

History[edit]

Pierre de Fermat gave a criterion for numbers of the form 3a+1 to be a sum of 3 squares essentially equivalent to Legendre's theorem, but did not provide a proof. N. Beguelin noticed in 1774^[1] that every positive integer which is neither of the form 8n + 7, nor of the form 4n, is the sum of three squares, but did not provide a satisfactory proof.^[2] In 1796 Gauss proved his Eureka theorem that every positive integer n is the sum of 3 triangular numbers; this is trivially equivalent to the fact that 8n+3 is a sum of 3 squares. In 1797 or 1798 A.-M. Legendre obtains the first proof of his 3 square theorem.^[3] In 1813, A. L. Cauchynotes^[4] that Legendre's theorem is equivalent to the statement in the introduction above. Previously, in 1801, C. F. Gauss had obtained a more general result,^[5] containing Legendre theorem of 1797-8 as a corollary. In particular, Gauss counts the number of solutions of the expression of an integer as a sum of three squares, and this is a generalisation of yet another result of Legendre,^[6] whose proof is incomplete. This last fact appears to be the reason for later incorrect claims according to which Legendre's proof of the three-square theorem was defective and had to be completed by Gauss.^[7]

With Lagrange's four-square theorem and the two-square theorem of Girard, Fermat and Euler, the Waring's problem for k = 2 is entirely solved.

Proofs[edit]

The "only if" of the theorem is simply because modulo 8, every square is congruent to 0, 1 or 4. There are several proofs of the converse. One of them is due to J. P. G. L. Dirichlet in 1850, and has become classical.^[8] It requires three main lemmas:

the quadratic reciprocity law,
Dirichlet's theorem on arithmetic progressions, and
the equivalence class of the trivial ternary quadratic form.

Relationship to the four-square theorem[edit]

This theorem can be used to prove Lagrange's four-square theorem, which states that all natural numbers can be written as a sum of four squares. Gauss^[9] pointed out that the four squares theorem follows easily from the fact that any positive integer that is 1 or 2 mod 4 is a sum of 3 squares, because any positive integer not divisible by 4 can be reduced to this form by subtracting 0 or 1 from it. However, proving the three-square theorem is considerably more difficult than a direct proof of the four-square theorem that does not use the three-square theorem.