交换排序之快速排序

应用交换排序思想的另一种经典排序算法是快速排序，快速排序的思想可以大致分成两大部分，一部分是利用分治策略的递归算法，另一部分是根据随机选择元素作为基准对整个数组进行的划分。算法先实现对数组进行划分，分成两个子数组，左边的子数组元素都比基准元素小，右边的子数组元素都比基准元素大。然后再对这两个子数组递归的进行划分，直到最后数组中只剩下一个元素。

数组划分

我们使用一个例子来说明对数组的划分过程
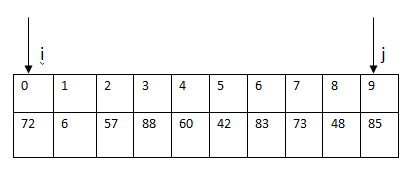
给定一个数组如下

选择第一个元素$A[0]$作为基准元素。$X=A[0]$。

定义两个变量$i=0, j=A.length-1$

如果$i<j$，首先判断$A[j]$与基准$X$的大小关系，例子中有$A[9]>X$，则该元素比基准大，放在基准后面不动，只需将$j$作$j--$运算向前移一位。接着判断$A[j]=A[8]=48<72$，小于基准的数应该放在前面，因此我们做$A[i]=A[j]$即$A[0]=A[8]=48$，（这个时候不需要交换$A[i]$与$A[j]$，因为我们已经将$A[0]$作为基准保存起来了，即使$A[0]$元素被替换掉也没有关系）。然后将$i$向后移一位

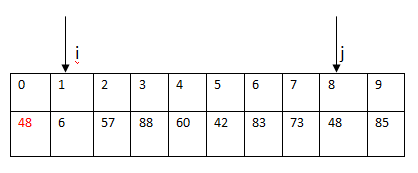
到这里，数组中元素$A[j]=A[8]$已经被放到了第一个位置，所以我们这时候不移动$j$下标的愿意是因为后面如果找到比基准大的元素还要放在这里。
，下标$i$指向$A[1]=6$这个元素，将$6$与基准$72$比较，有$6<72$，比72小的元素就是放在前面的，所以不加操作继续将下标$i$后移，到$57$这个元素时的情况与$6$相同，继续后移$i$，到$i=3$时，有$A[i]=88>72$，做操作$A[j]=A[8]=A[i]=A[3]$，则有

同样的，这里我们不再动下标$i$（因为这个元素已经被放到了后面，这个位置一会要放比基准小的本来在数组后面的元素）。向前移动下标$j$，到元素73位置处，有$73>72$，所以不做任何操作，再向前移动下标$j$到$83$位置处还是同样的不动，直到下标$j$到达位置$42$位置处，发现$42<72$，做操作$A[i]=A[3]=A[j]=A[5]$

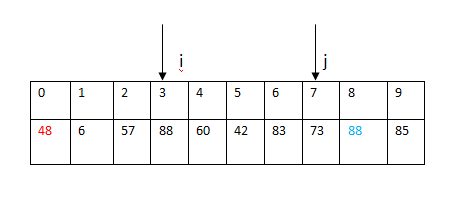
到这里之后同样的不再移动下标$j$（这个位置留着放前面过来的大于基准的元素），向后移动$i$到元素$60$的位置，因为$60<72$所以不做操作继续向后移动$i$，到这里之后有$i=j=5$不再满足$i<j$。此时将基准元素放在$A[5]=72$，完成划分并返回下标 i <script type="math/tex" id="MathJax-Element-15493">i</script>，成功将数组划分成两个子数组。

递归调用

接下来有了对数组划分的算法之后，直接根据返回的两个子数组之间的划分下标两次递归调用这个数组划分算法，直到每个数组中都只剩下一个元素。

Java实现的代码如下

public class QuickSort {

    public static void main(String []args){
        int[]A={72,6,57,88,60,42,83,73,48,85};
        quickSort(A,0,A.length-1);

        for(int i=0;i<A.length;i++){
            System.out.println(A[i]);
        }
    }

    public static void quickSort(int[] A,int l,int r){      
        if(l<r){
            int X=A[l];
            int i=l;
            int j=r;
            while(i<j){
                while(i<j && A[j]>=X){
                    j--;
                }
                if(i<j){
                    A[i]=A[j];
                    i++;
                }
                while(i<j && A[i]<=X){
                    i++;
                }
                if(i<j){
                    A[j]=A[i];
                    j--;
                }
            }
            A[i]=X;
            quickSort(A,l,i-1);
            quickSort(A,i+1,r);
        }

    }

}

上述代码可以进行简单的简化，但是为了清楚的表达整个算法的过程，我没有对其进行调整。这样可以分别对应每一部操作过程来更清楚的理解快速排序的过程。
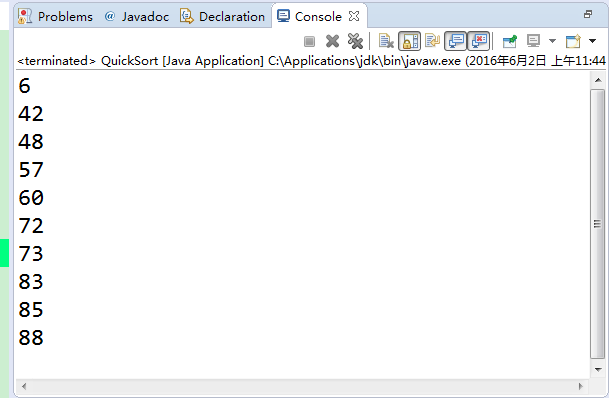
输出结果

LZ也是菜鸟一枚，正在努力学习中，如果哪里说的有错误的地方还劳烦大神指出来我会认真改正的哦