单变量线性回归
假设方程:(构造矩阵x时,使x(:,1)=1)
代价函数:(y是训练集中实际值,hθ(x)是预测值)
利用gradient descent(梯度下降),一步步迭代求出使代价函数最小的θ,**注意:对于单变量,θ是二维的
data = load('ex1data1.txt');
X = data(:, 1);
y = data(:, 2);
m = length(y); % number of training examples
plotData(X, y);
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
% Some gradient descent settings
iterations = 1500;
alpha = 0.01;
%compute theta
for iter = 1:iterations
temp1=theta(1)-alpha/m*sum((X*theta-y).*X(:,1));
temp2=theta(2)-alpha/m*sum((X*theta-y).*X(:,2));
theta(1)=temp1;
theta(2)=temp2;
end
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure运行结果:
ex1data1.txt部分数据:
多变量线性回归
多变量线性回归与单变量大同小异,只是θ维度变为n*1,在用gradient descent方法计算时,用一个循环计算即可。
temp=zeros(size(theta,1),1);
for i=1:size(theta,1),
temp(i)=theta(i)-alpha/m*sum((X*theta-y).*X(:,i));
end;
for i=1:size(theta,1),
theta(i)=temp(i);
end;在迭代中可以计算出每一次迭代损失函数的值(即每个theta对应的J的值)然后画出来。
J=(X*theta-y)'*(X*theta-y)/2/m;
随着迭代次数增加,J逐渐减小,alpha值增大,J减小速度越快,但是,当alpha很大时J不会一直减小会出现波动。








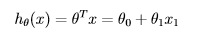
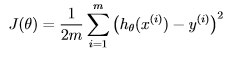
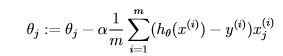

















 5874
5874

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








