Supervised Descent Method Face Alignment 代码下载 和 算法研究 之一

1 主要内容：
Supervised Descent Method and its Applications to Face Alignment算法研究。

2代码彩蛋：我问了好久，xxiong好心人发给我的，希望能对你们学习有帮助：
低调下载：
http://humansensing.cs.cmu.edu/xxiong/mexintraface1.3.1%28release%29.zip。
注意杜绝一切商业用途，如果需要商业用途，请联系作者本人！！

3本文分为几个部分：
(1)解决什么问题
(2)具体理论方法是什么
(3)具体实现步骤

(1)解决什么问题
上一篇文章newton方法，请看具体实现，

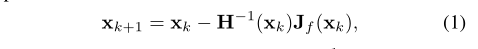
牛顿法目的是求f(x)最小值。然后改成求f’(x)=0。
迭代n次上图公式1，直到Xk+1 - Xk收敛到0.0001
or 其他非常小大于0的值。
而公式1中 f’(x)是上图中J(f(Xk))函数， 而f”(x)是H(Xk).
下图为该方法：

是牛顿迭代的梯度方向。
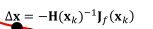
更多内容请看：上一篇牛顿法-最优方法。
我们知道牛顿法：要满足在定义域内二次可微，hession矩阵正定。

而在计算机背景下，运用newton method有三个问题:
1 Hession矩阵在最小值的局部是正定的，但在其他地方可能不正定。
因为只有Hession矩阵正定，初始值才能收敛到局部值。

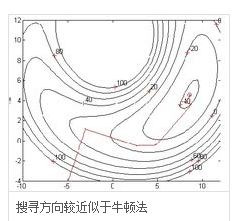
上图可知：搜索方法是凹方向，是梯度 or Hession矩阵的相反方向，只有Hession矩阵正定，即每个Hession矩阵每个特征值大于零，才会沿着梯度相反方向，即沿着曲线的凹方向(梯度方向是曲线的凸方向)，收敛到局部极值点。

2Hession矩阵需要二次可微。但在计算机视觉下，x比如sift特征，是一个不可微的图像操作，即sift特征是离散的。在这种情况下，我们只能用数值逼近Hession矩阵 or 梯度，但这样做计算成本很大。

3Hession矩阵的维数可能很大。而Hession矩阵的逆矩阵计算的时间复杂度是O(n^3)，空间复杂度O(n^2)，n是矩阵维数，计算量和空间内存都需要很大，即使用 L-BFGS，计算成本仍然很大。

所以作者提出了a Supervised Descent Method (SDM),来求非线性的最小平方差。
在训练阶段：
通过最小化所有样本的非线性平方差函数之和，
学习许多梯度方向组成的梯度序列。
在测试阶段:
SDM minimizes 非线性平方差函数，
使用训练时训练的梯度方向，
再也不用计算 the Jacobian nor the Hessian矩阵 。

(2)Supervised Descent Method(SDM）具体理论原理是什么？
这里研究的SDM是对face alignment application.

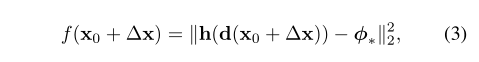
上公式中:
1 d代表一个人脸图片的m个像素，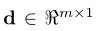
2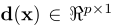
d(x)代表一个图片的66个标点。
3 h是特征抽取函数(比如sift特征抽取),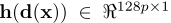
h(d(x))是在标点d(x)周围抽取的128维的sift特征。

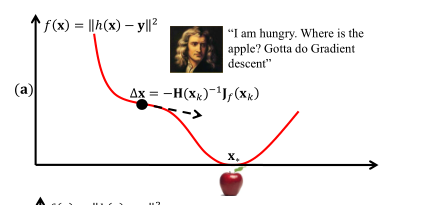
4上图
(a)图在训练期间，假设66个标记是已知，我们称之为X*
(b)图 先用检测到人脸（蓝色矩阵框),再用所有样本平均shape,作为X0,初始化位置。
人脸匹配(face alignment）,是极小化公式(3).