奇异值分解SVD

         本总结是是个人为防止遗忘而作，不得转载和商用。

关于奇异值分解的名字：

         第一次看“奇异值分解”时真是超不知所以。不过它的英文名字是Singular Value Decompostion。而Signular是“突出的、奇特的、非凡的”的意思，于是用“优值分解”的这个名字好像更贴切些，而且“优值分解”这个名字的第一印象就比“奇异值分解”更让人容易接受。

什么是奇异值分解：

         假设A是一个m*n的实矩阵，那么一定存在这样一个分解使得：

                   A_m*n= U_m*mΣ_m*nV^T_n*n

              其中，U和V都是单位正交方阵，Σ是一个只有45°对角线上存在非零值的矩阵。

         这时，称这样一个分解为奇异值分解；

                   Σ对角线上的元素σi是矩阵A的奇异值；

                   U的第i列称为A的关于σi的左奇异向量；

                   V的第i列称为A的关于σi的右奇异向量；

         看了上面的介绍是不是还不明所以，没关系，下面我会继续解释，总之知道这样一种分解是奇异值分解就是了。

                   PS：就好像对于一个数，我总能把它写成3个数相乘似得，对于一个矩阵，我总能通过某种方法把它分解成这样的形式，你别管我用的什么方法，但你总的承认我能把它分解对吧。

奇异值分解定义的解释：

         为了对奇异值分解更有概念，我们来对定义举个小例子。

         对于一个矩阵A

                  

         我总能通过某种方式将其分解成A = UΣV^T的样子（你别管我怎么分解的），其中UΣV如下：

        

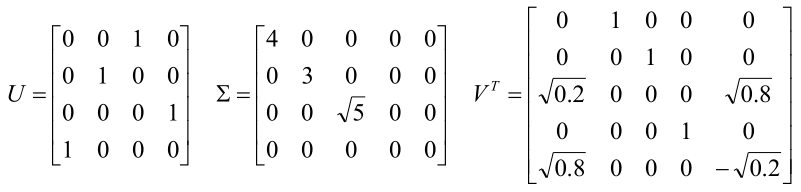
         且U和V是单位正交方阵，即：矩阵U和V满足式子：

                  U^TU = I，V^TV= I

         Σ是只有45°对角线上有非零元素的矩阵（注意是45°对角线）。

         这时，这样的分解就是奇异值分解。

         Σ中45°对角线上的那三个非零元素就是矩阵A的奇异值。

奇异值分解有什么作用：

         现在我们已经知道，通过奇异值分解可以把矩阵A分解成UΣV三个矩阵相乘的形式，但奇异值分解到底有什么用呢？

为了说明这个，我假设A是个m*n的矩阵，那经过奇异值分解后，U就是m*m的矩阵，Σ是m*n的矩阵，V是n*n的矩阵（为什么？因为根据定义U和V都是方阵，如果还看不懂，那你需要复习下矩阵的乘法了。）

         然后，把矩阵M的每一列用一个列向量u_i表示，于是矩阵U我就可以写成

                  U = [u₁, u₂, …, u_i,…, u_m]

         同理，把V的每一行用一个行向量v_i表示后，矩阵V就可以写成

                  V = [v₁, v₂, …, v_i,…, v_n]

         而Σ因为只有对角线上有非零元素，所以我们用σi表示Σ上每一行的非零元素。

         这时，如果我们只取这三个矩阵的前k个元素，就有：

                  A = UΣV = u₁σ₁v₁ + u₂σ₂v₂ + … + u_kσ_kv_k

             这意味着什么？

         这意味着我们将m*n这样一个维度的矩阵A降成了k*k维！

         当然这样一来降维后的矩阵和原来的矩阵不同，即：数学结果不同。

不过在实际应用中，这个降维后的矩阵其效果是和原矩阵一样的！

例子：

         下面我写的SVD压缩图片的效果和代码(restore函数来自于皱博老师)

         首先是效果。

         原图：

         使用SVD分解压缩后后：

         上面四张图是分别取前1、10、40、80个特征向量的结果。

         可以看到，取前80个特征向量就已经可以把原图恢复的差不多了，而代码中经过mtr.shape = (649, 2886)转换之后可是有649个特征向量的。

         下面是代码，其中我的疑问也在里面，如果有谁知道答案的话，不知可否在评论里告知一下，不胜感激。

#-*-coding:utf-8-*-

# 关于 svd 压缩图片的问题

# 问题0：

#   在 restore 函数的

#      b = a.astype('uint8')

#   前加上如下3行可以解决本人的实验图片经svd 压缩并使用 restore 函数保存后图片太扁的问题

#      n = n / 3

#      a.shape = (m, n, 3)

#      a.transpose()

#   但即使是以参数的方式传入这个 3，但是不是还是太有针对性？

#

# 问题1：

#   上课时听老师讲 SVD 时说的的矩阵的2维的，而我使用

#      mtr = np.array(im)

#   将 im 转换成矩阵后，矩阵是3维的，矩阵的信息如下：

#      # Mtr   --  ndim:3, shape:(649, 962, 3), size:1873014

#   这是为什么？

#   是本来就是这样，需要我在转换成矩阵后在将其处理2维的吗？还是什么？

#

# 问题2：

#   在问题1的基础上，图片读取成矩阵后如何处理这个矩阵？

#   我这边如代码所示，在使用下面两行代码

#      mtr.shape = (649, 2886)

#      mtr.transpose()

#   处理图片，最后使用 defrestore 保存出来的图片会特别的扁。

#

# 问题3：

#   有没有什么方法可以

#      "读取图片 -> 将图片数据转换成矩阵 -> 使用svd -> 代入 def restore"

#   而不是像我写的

#      "读取图片 -> 将图片数据转换成矩阵 -> 将矩阵处理成秩为2的矩阵 -> 使用svd -> 代入 def restore"

#  

# 其他：我使用的图片在 http://pan.baidu.com/s/1i4GLeSH

 

import os

import sys

import Image

import numpy as np

 

BASIC_PATH = sys.path[0]

 

def restore(sigma, u, v, k):

    m= len(u)

    n= len(v[0])

    a= np.zeros((m, n))

   for k in range(k+1):

       for i in range(m):

           # a[0] = sigma 的第一个 * u 的第一列 * v 的第一行

           # a[1] = sigma 的第二个 * u 的第二列 * v 的第二行

           # 以此类推

           a[i] += sigma[k] * u[i][k] * v[k]

         #下面三行是我自己添加的，否则保存出来的图片会太扁

    n= n / 3

   a.shape = (m, n, 3)

   a.transpose()

    b= a.astype('uint8')

   Image.fromarray(b).save("svd_" + str(k) + ".jpg")

 

 

# 读取图片

im = Image.open("%s/1.jpg" %BASIC_PATH)

# 将图片信息转换成矩阵

mtr = np.array(im)

# Image -- format:JPEG, size:(962, 649), mode:RGB

print 'Image\t--\tformat:%s, size:%s,mode:%s' % (im.format, str(im.size), im.mode)

# Mtr  --  ndim:3, shape:(649, 962, 3),size:1873014

print 'Mtr\t-- \tndim:%s, shape:%s,size:%d' % (str(mtr.ndim), str(mtr.shape), mtr.size)

 

# 这里矩阵的秩是3，将其转成2

mtr.shape = (649, 2886)

mtr.transpose()

# svd

# 这里 U 和 VT 是秩为 2 的矩阵，sigma 矩阵的秩为 1

U, sigma, VT = np.linalg.svd(mtr,full_matrices=False)

# 取前 k 个特征向量

k = 100

# 保存图片

restore(sigma, U, VT, k)

im = Image.open("%s/svd_%s.jpg" %(BASIC_PATH, k))

im.show()