Bellman-Ford algorithm

Bellman-Ford算法描述：

1. Bellman-Ford算法能在一般的情况下解决单源最短路径问题（即允许存在负权边，而Dijkstra算法不允许存在负权边）。

2. Bellman-Ford算法的结果是一个bool值，表明图中是否存在着从源点s可达的负权回路。若不存在这样的回路，算法将给出从源点s到图G任意顶点v的最短路径dist[v]；若存在这样的回路，说明该问题无解，即存在一个从源点s到某一个点的最短路径趋向于负无穷（无限循环可得）。

Bellman-Ford算法过程（伪代码）：

<span style="font-size:18px;">Bellman-Ford(G,w,s) ：boolean                   //图G ，边集 函数 w ，s为源点  
       for each vertex v ∈ V（G） do           //1阶段 初始化
           dist[v] ←+∞  
       dist[s] ←0;                             //1阶段 初始化结束  
       for i=1 to |v|-1 do                      //2阶段 开始，外循环进行
          for each edge（u,v） ∈E(G) do        //对每条边进行松弛  
             If dist[v]> dist[u]+ w(u,v) then   //松弛判断  
                dist[v]=dist[u]+w(u,v)          //2阶段结束 松弛操作 
       for each edge（u,v） ∈E(G) do           //判断是否存在从源点s可达的负权值回路
           If dist[v]> dist[u]+ w(u,v) then  
             Exit false                         //若存在，问题无解，返回False  
       Exit true                                //若不存在，返回True，存在从源点s到各个点的最短路径</span>

Bellman-Ford算法思想：

1. 首先可以确定的是，图G的任意一条最短路径既不能包含负权值回路，也不能包含正权值回路，因此它最多包含(|v|-1)条边。

2. 从源点s可达的所有顶点如果存在最短路径，则这些最短路径构成一个以s为根的最短路径树。Bellman-Ford算法的迭代松弛操作，实际上就是按顶点距离s的层次，逐层生成这颗最短路径树的过程：

在对每条边进行第一遍松弛的时候，生成了从s出发，层次至多为1的那些树枝，也就是说找到了与s至多有1条边相连的那些顶点的最短路径；

在对每条边进行第二遍松弛的时候，生成了从s出发，层次至多为2的那些树枝，也就是说找到了与s至多有2条边相连的那些顶点的最短路径；

... ...以此类推；

因为最短路径最多包含(|v|-1)条边，所以只需循环(|v|-1)次。

3. Bellman-Ford算法构造一个最短长度数组序列dist¹[u]，dist²[u]，dist³[u]，... ，dist^n-1[u]。其中：

dist¹[u]为从源点s到终点u的只经过1条边的最短路径长度，并有dist¹[u]=edge[s][u]；

dist²[u]为从源点s到终点u的最多经过2条边的最短路径长度；

dist³[u]为从源点s到终点u的最多经过不构成负权值回路的3条边的最短路径长度；

... ...

dist^n-1[u]为从源点s到终点u的最多经过不构成负权值回路的n-1条边的最短路径长度；

算法的最终目的是计算出dist^n-1[u]，为源点s到u的最短路径长度。

4. 在Bellman-Ford算法中判断是否存在从源点s可达的负权值回路的方法：

思路：在求出dist^n-1[u]之后，再对每条边<u,v>判断一下：加入这条边后，是否会使得s到顶点v的最短路径再缩短，即判断：dist[u]+w[u,v]<dist[v] 是否成立，如果成立，则说明存在从源点s可达的负权值回路。

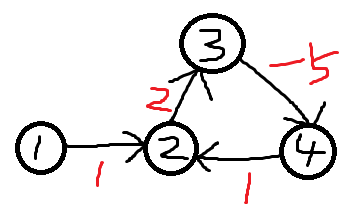
例如：

更新迭代n-1后，dist[2]=1,dist[4]=-2；

枚举到w(4,2)时：dist[4]+w(4,2)<dist[2]，即出现负权值回路。

Bellman-Ford算法优化：

如果在某一遍的迭代中，并没有进行松弛操作，说明该遍迭代所有边都没有松弛，可以证明， 至此以后，所有的边都不需要再松弛，因此可以提前结束迭代过程。所以优化方法就是设置一个bool变量。

Bellman-Ford(G,w,s) ：boolean                   //图G ，边集 函数 w ，s为源点  
       for each vertex v ∈ V（G） do           //1阶段 初始化
           dist[v] ←+∞  
       dist[s] ←0;                             //1阶段 初始化结束  
       for i=1 to |v|-1 do                      //2阶段 开始，外循环进行
          bool flag=false;
          for each edge（u,v） ∈E(G) do        //对每条边进行松弛  
             If dist[v]> dist[u]+ w(u,v) then   //松弛判断  
                dist[v]=dist[u]+w(u,v)          //2阶段结束 松弛操作 
                flag=true;
           if(!flag)
	      break;
       for each edge（u,v） ∈E(G) do           //判断是否存在从源点s可达的负权值回路
           If dist[v]> dist[u]+ w(u,v) then  
             Exit false                         //若存在，问题无解，返回False  
       Exit true                                //若不存在，返回True，存在从源点s到各个点的最短路径

ps：优化后的算法在处理有负权回路的测试数据时，由于每次都会有边被松弛，所以flag每次都会被置为true，因而不可能提前终止外层循环。