Poj3241 Object Clustering

Poj3241 Object Clustering

Position：

• http://poj.org/problem?id=3241

---

List

Description

• 大意：求曼哈顿距离最小生成树上第k大（第n-k小）的边。

Knowledge

参考曼哈顿距离最小生成树
http://blog.csdn.net/yjpyjp2014/article/details/52180707

Solution

分析：
1.由上面资料可知，每45度的范围只算一个最近点
2.看下面一种情况：
　　　　　　
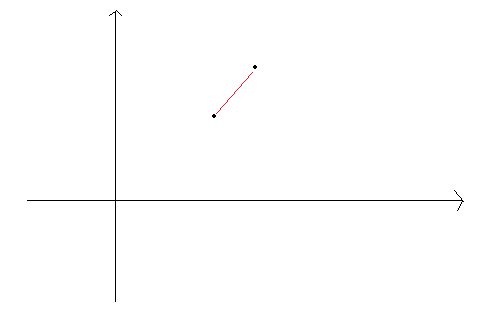
对于下面那个点，上面的点在它的右上方。而它又在上面的点的左下方，故我们只需计算左上和右上，即角[0,180]的范围，每45度一个，每个点4个，故边数不超过4×n。
3-1.为了写代码的方便，我们每次将点翻转，只计算[45,90]范围的点。翻转：①第一次不翻②第二次将一个点的x与y交换(即沿y=x翻转，原本在[0,45]的点翻到了[45,90])③将x=-x，沿x=0翻转，左上翻到右上④
3-2.ZYT的写法(可能容易理解一点):我们只需考虑在一块区域内的点，其他区域内的点可以通过坐标变换“移动”到这个区域内。为了方便处理，我们考虑在y轴向右45度的区域。在某个点A(x0,y0)的这个区域内的点B(x1,y1)满足x1≥x0且y1-x1>y0-x0。这里对于边界我们只取一边，但是操作中两边都取也无所谓。那么|AB|=y1-y0+x1-x0=(x1+y1)-(x0+y0)。在A的区域内距离A最近的点也即满足条件的点中x+y最小的点。因此我们可以将所有点按x坐标排序，再按y-x离散，用线段树或者树状数组维护大于当前点的y-x的最小的x+y对应的点（也就是维护区间最小值）。时间复杂度O(NlogN)。至于坐标变换，一个比较好处理的方法是第一次直接做(R1==R5)；第二次沿直线y=x翻转，即交换x和y坐标(R2==R6)；第三次沿直线x=0翻转，即将x坐标取相反数(R7==R3)；第四次再沿直线y=x翻转(R8==R4)。注意只需要做4次，因为边是双向的。
　　　　　　　　　　　　　
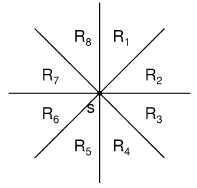
4.对于点(x,y)如果有一个点(x1,y1)在它的(45,90)，只要满足y1-x1>y-x(证明：即用一条斜率为45的直线，过这个点，比截距的大小y=x+b，y-x=b，平面图知识qaq~)
5.按x坐标排序，从后往前扫，值域(y-x)树状数组，w记录的是曼哈顿距离，pos记录第几个点。

Notice

1.这是一个反的树状数组，c[i]记录i~i+lowbit(i)-1
2.因为只要求x~m的最小值，用树状数组可以

Code

// <ObjectClustering.cpp> - 08/11/16 16:35:38
// This file is made by YJinpeng，created by XuYike's black technology automatically.
// Copyright (C) 2016 ChangJun High School, Inc.
// I don't know what this program is.

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#define MOD 1000000007
#define INF 1e9
#define EPS 1e-10
using namespace std;
typedef long long LL;
const int MAXN=10010;
const int MAXM=100010;
inline int max(int &x,int &y) {return x>y?x:y;}
inline int min(int &x,int &y) {return x<y?x:y;}
inline int getint() {
    register int w=0,q=0;register char ch=getchar();
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    if(ch=='-')q=1,ch=getchar();
    while(ch>='0'&&ch<='9')w=w*10+ch-'0',ch=getchar();
    return q?-w:w;
}
int n,m,k,tot,cnt,x,pos;
int f[MAXN],hs[MAXN],t[MAXN];
struct Point{
    int x,y,id;
    void read(){x=getint();y=getint();}
    friend bool operator < (const Point &a,const Point &b) {
        return a.x==b.x?a.y<b.y:a.x<b.x;
    }
}p[MAXN];
struct Edge{
    int u,v,w;
    friend bool operator < (const Edge &a,const Edge &b){
        return a.w<b.w;
    }
}e[MAXN*4];
struct Bit{
    int w,pos;
    void Pre(){pos=-1,w=INF;}
}b[MAXN];
inline int Find(int x){return x==f[x]?x:f[x]=Find(f[x]);}
inline int Lowbit(int x){return x&(-x);}
int Dis(int a,int b){
    return abs(p[a].x-p[b].x)+abs(p[a].y-p[b].y);
}
int Query(int x){
    int M=INF,pos=-1;
    for(int i=x;i<=m;i+=Lowbit(i))
        if(b[i].w<M)M=b[i].w,pos=b[i].pos;
    return pos;
}
void Update(int x,int M,int pos){
    for(int i=x;i;i-=Lowbit(i))
        if(M<b[i].w)b[i].w=M,b[i].pos=pos;
}
void Insert(int u,int v,int w){
    e[++cnt].u=u;e[cnt].v=v;e[cnt].w=w;
}
void Caledge(){
    sort(p+1,p+1+n);
    for(int i=1;i<=n;i++)hs[i]=t[i]=p[i].y-p[i].x;
    sort(hs+1,hs+1+n);
    m=unique(hs+1,hs+1+n)-hs;
    for(int i=1;i<=m;i++)b[i].Pre();
    for(int i=n;i>=1;i--){
        x=lower_bound(hs+1,hs+1+m,t[i])-hs+1;
        pos=Query(x);
        if(pos!=-1)Insert(p[i].id,p[pos].id,Dis(i,pos));
        Update(x,p[i].x+p[i].y,i);
    }
}
void Kruskal(){
    sort(e+1,e+1+cnt);tot=0;
    for(int i=1;i<=n;i++)f[i]=i;
    for(int i=1;i<=cnt;i++){
        f[e[i].u]=Find(f[e[i].u]);
        f[e[i].v]=Find(f[e[i].v]);
        if(f[e[i].u]!=f[e[i].v])f[f[e[i].u]]=f[e[i].v],tot++;
        if(tot==k){printf("%d",e[i].w);break;}
    }
}
int main()
{
    freopen("ObjectClustering.in","r",stdin);
    freopen("ObjectClustering.out","w",stdout);
    n=getint();k=n-getint();
    for(int i=1;i<=n;i++)p[i].read(),p[i].id=i;
    for(int j=1;j<=4;j++){
        if(j==2||j==4)
            for(int i=1;i<=n;i++)swap(p[i].x,p[i].y);
        else if(j==3)
            for(int i=1;i<=n;i++)p[i].x=-p[i].x;
        Caledge();
    }
    Kruskal();
    return 0;
}

感谢

Friend ZYT的大力支持