最优二分搜索树

构建最优二分搜索树

问题描述：

       首先看个例子，如果有S = {5,7,10,12,14,15,18}，我们可以构建一个二分搜索树，所谓二分搜索树（Binary Search Tree），就或者是一棵空树，或者是具有下列性质的二分树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二分搜索树。现在，我们可以构建一下两种树：

                         

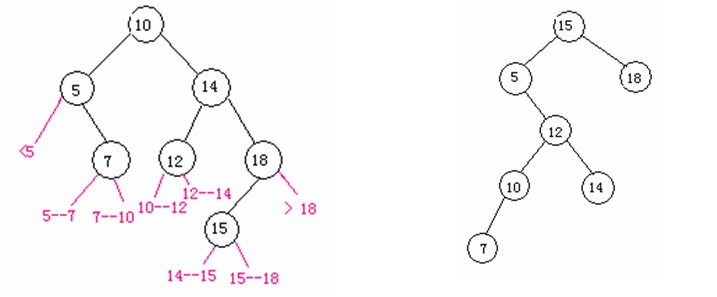
       现在问题来了，如果在我们的搜索中15~18范围搜索的次数为80%，节点5的搜索次数为10%，其余的节点和节点以外的范围搜索次数频率相等，共计10%。显而易见，两种不同结构的二分搜索树的效率大不一样。在此，结合每个搜索到的节点和范围的频率（记为p[1：n]，q[0：n]）我们给出搜索树的总耗费公式为：

        

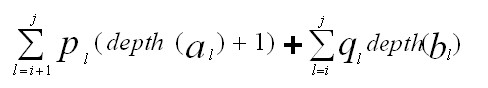
       这里depth(a_l)为a_l在该树中的深度，depth(b_l)为b_l在该树中的深度。

       如今的问题就是，对于一个给定的序列，{b₀，a₁，b₁……a_n，b_n}，其中a₁，a₂……a_n是实节点，b₀，b₁，b₂……b_n是虚节点（就是二分搜索树最终找不到实节点的范围），如何找出并构建一个总耗费最小的二分搜索树？

问题求解：

     分析：

            假定T₀是棵最优二分搜索树，它的根是a_k（第k小的数）。则a_k的左子树中必然包含了{a₁…a_k-1}， a_k的右子树中必然包含了{a_k+1…a_n}。而且，左子树一定是关于{a₁…a_k-1}的最优二分搜索树，右子树一定是关于{a_k+1…a_n}的最优二分搜索树。（否则，用更优的子树代替当前的子树，其总耗费比T₀的更小，矛盾。）

       现在考虑二分搜索树问题的性质，

       ① 根据二分搜索树的性质，任何一棵子树中结点的编号都是连续的。而且，最优树中的任何一棵子树，也必然是关于子树中结点的最优树。因此，最优二分搜索树具有最优子结构性质。

       ② 这样，若规模为m≤n-1的最优子树均已知，就可以通过逐一计算以a₁，a₂，…，a_n为根的树的耗费，来确定（使耗费达到最小的）根a_k并找出最优二分搜索树。

       在上述计算中，规模较小的最优子树在计算中要多次被用到，故该问题具有高度重复性。

       综合 ①和②的特性，我们就考虑动态规划来求解这个问题。

 

       在所有由结点b_i，a_i+1，b_i+1，…，a_j，b_j构成的树中，把耗费最小的树记为T_ij。（注意该树中不含a_i但含b_i）。

       若由结点b_i，a_i+1，b_i+1，…，a_j，b_j构成的树以a_k作为根 (i+1≤k≤j)，

           则b_i，a_i+1，b_i+1，…，a_k-1，b_k-1必然在其左子树中，

           则b_k，a_k+1，b_k+1，…，a_j，b_j必然在其右子树中，

       以a_k为根的树有很多，但其中耗费最小的树必然是以T_i,k-1为其左子树，以T_k,j为其右子树。

       记c_ij是最优子树T_ij的耗费， 则ci_,k-1是最优子树T_i,k-1的耗费，c_k,j是最优子树T_k,j的耗费。

       考察以a_k (i+1≤k≤j)为根、由结点b_i，a_i+1，b_i+1，…，a_j，b_j构成的、耗费最小的树的总耗费：根据上述讨论，

该树的左子树必然是T_i,k-1，右子树必然是T_k,j 。该树的总耗费可分为三部分：左子树、右子树和根所产生的耗费。

       紧接着就将T_i,k-1和T_k,j接到a_k上，此处与每个左右子树中节点来说，搜索的耗费都增加了，因为每个节点的深度都增加了1，因此，引入一个公式，来表示子树在接入根节点的时候增加的耗费，

             

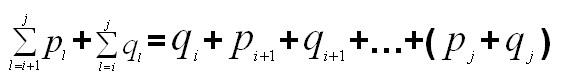
        由于T_i,k-1作为左子树接到结点a_k之下时，其耗费增加w_i,k-1，故左子树的耗费为：c_i,k-1+ w_i,k-1，

        同理，右子树的耗费为：c_k,j+w_k,j，

        由于根a_k的深度为0，按定义，根的耗费为p_k。

        因此，以a_k 为根、耗费最小的树的总耗费为：c_i,k-1+ w_i,k-1+c_kj+w_k,j+p_k。

        注意到，

                   w_i,k-1=q_i+p_i+1+q_i+1+…+p_k-1+q_k-1，

                   w_k,j=q_k+p_k+1+q_k+1+…+p_j+q_j，

        从而有w_i,k-1+w_kj+p_k = q_i+p_i+1+q_i+1+…+p_k-1+q_k-1+ p_k +q_k+p_k+1+q_k+1+…+p_j+q_j = w_ij。

        由此得到,以a_k 为根、耗费最小的树的总耗费为：c_i,k-1+c_kj+w_i,j由于p_i（i=1,2,…,n）和 qj（j=0,1,2,…,n）在初始时已经知道，因此若w_i,j-1已知，则根据w_i,j= w_i,j-1+p_j + q_j可以计算出w_ij。故当c_i,k-1与c_kj已知时，以a_k 为根的树的最小总耗费在O(1)时间就可以计算出来。

        这样，分别计算以a_i+1，a_i+2，…，a_j为根、含有结点b_i，a_i+1，b_i+1，…，a_j，b_j的树的最小总耗费，再从中选出耗费最小的树，即可得最优子树T_ij。

        因此，最优子树T_ij的耗费c_ij= {c_i,k-1+c_kj+w_ij}。

算法描述：

        递推求c_ij及记录T_ij的根的算法

        初始时 w_ii←q_i(i=1,2,…,n)；c_ii←0；/*∵空树T_ii耗费为0（i=1,2,…,n）。*/

        for l←1 to n do /*计算规模为l（树中真实结点个数）的最优二分搜索树，从含1个结点直算到含n个结点*/

            { for i←0 to n-l do    /*真实结点个数为l个的树共有(n-l+1)个，i为树中结点起始下标，从0直到n-l。*/

                 {   j←i+l;                     /* j为树中最后一个结点的下标*/

                     w_i,j←w_i,j-1+p_j + q_j ;  /*计算出规模为l (l=j-i)、当前所需的wi,j*/

                     c_ij← {c_i,k-1+c_kj+w_ij};    /*在前一轮或前几轮，规模小的c_i,k-1和c_kj已计算出来了*/

                     r_ij←k’;      /*k’为使得{c_i,k-1+c_kj+w_ij}为最小的k值*/

                  }                 /*即ak’是最优子树T_ij的根，记录在案*/

             }

 

        构建最优二分搜索树，

        设T_ij的根为a_k (r_ij记录到的值是k)，则从根开始建结点。

        Build-tree(i,j,r,A)                    /*建立最优子树T_ij*/

        {

           If i≥j return null;

           pointer←newnode(nodetype);

           k←r_ij;                               /*必有i < k ≤j*/

           pointer_key-value←A[k];             /*A[k]即ak*/

           pointer_leftson←Buildtree(i,k-1,r,A); /*建立最优左子树T_i,k-1*/

           pointer_rightson←Buildertree(k,j,r,A); /*建立最优右子树T_k,j*/

           return pointer;

        }

        调用Build-tree(0,n,r,A)则可以建成最优二分搜索树。

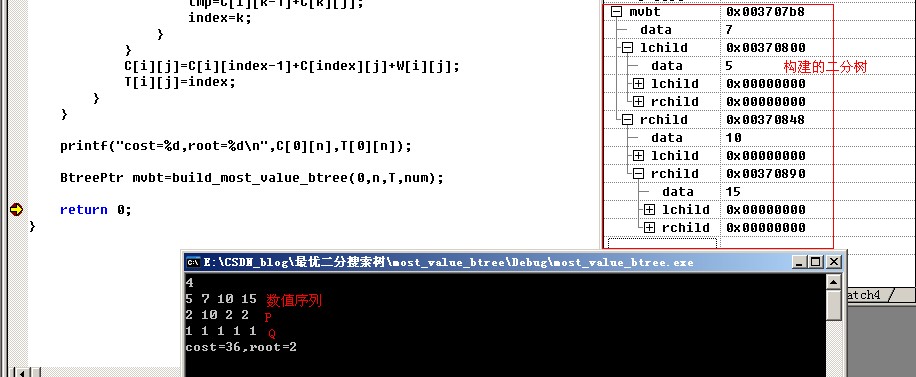
C语言实现与运行结果截图:

 

[cpp]  view plain copy

1. #include <stdio.h>  
2. #include <stdlib.h>  
3.   
4. #define     MAX_LEN     256  
5.   
6. typedef struct BtreeNode{  
7.     int data;  
8.     BtreeNode* lchild;  
9.     BtreeNode* rchild;  
10. }BtreeNode,*BtreePtr;  
11.   
12. BtreePtr build_most_value_btree(int st,int ed,int (*T)[MAX_LEN],int *num)  
13. {  
14.     if(st >= ed) return NULL;  
15.     BtreePtr  p;  
16.     p=(BtreePtr)malloc(sizeof(BtreeNode));  
17.     p->data=num[T[st][ed]];  
18.     p->lchild=build_most_value_btree(st,T[st][ed]-1,T,num);  
19.     p->rchild=build_most_value_btree(T[st][ed],ed,T,num);  
20.     return p;  
21. }  
22.   
23.   
24. int main()  
25. {  
26.     int index,tmp;  
27.     int n,i,j,k,l;  
28.     int P[MAX_LEN],Q[MAX_LEN];  
29.     int num[MAX_LEN],W[MAX_LEN][MAX_LEN],C[MAX_LEN][MAX_LEN],T[MAX_LEN][MAX_LEN];  
30.   
31.     while(1==scanf("%d",&n)){  
32.         if(n > 0){  
33.             for(i=1;i<=n;i++)  
34.                 scanf("%d",num+i);  
35.             for(i=1;i<=n;i++)  
36.                 scanf("%d",P+i);  
37.             for(i=0;i<=n;i++)  
38.                 scanf("%d",Q+i);  
39.             break;  
40.         }  
41.         printf("invalid n.\n");  
42.     }  
43.   
44.     //initial tabs  
45.     for(i=0;i<=n;i++){  
46.         W[i][i]=Q[i];  
47.         C[i][i]=0;  
48.     }  
49.   
50.     for(l=1;l<=n;l++)  
51.     {  
52.         for(i=0;i < n;i++){  
53.             j=i+l;  
54.             W[i][j]=W[i][j-1]+P[j]+Q[j];  
55.   
56.             //find the minium root  
57.             index=i+1;tmp=C[i][i]+C[i+1][j];  
58.             for(k=i+2;k<=j;k++){  
59.                 if(C[i][k-1]+C[k][j] < tmp){  
60.                     tmp=C[i][k-1]+C[k][j];  
61.                     index=k;  
62.                 }  
63.             }  
64.             C[i][j]=C[i][index-1]+C[index][j]+W[i][j];  
65.             T[i][j]=index;  
66.         }  
67.     }  
68.   
69.     printf("cost=%d,root=%d\n",C[0][n],T[0][n]);  
70.   
71.     BtreePtr mvbt=build_most_value_btree(0,n,T,num);  
72.   
73.     return 0;  
74. }