指派问题匈牙利解法以及其优化
本人第一次写blog,难免有不足之处,还请大家不吝指正。
1、问题的提出
简单的说,n个人恰好分别承担n个任务,每个人对于不同的任务效率不同;我们的目的就是为使任务完成效率尽可能的高。
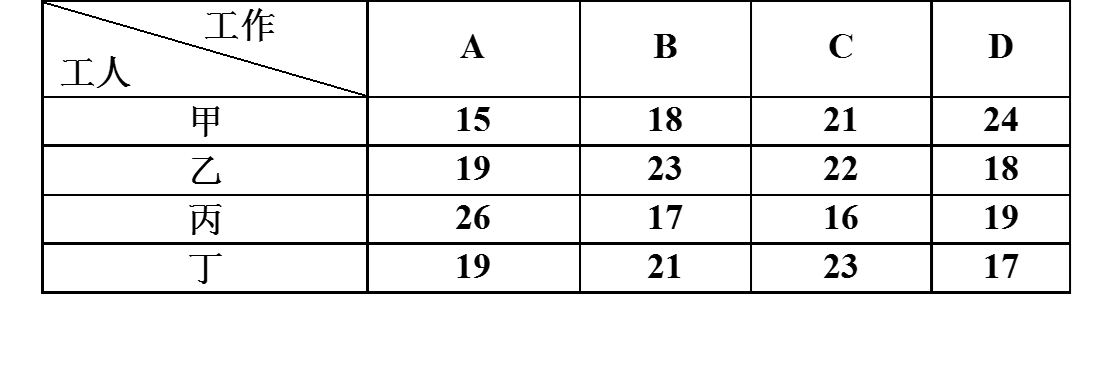
例如:有4个工人,要分别指派他们完成4项不同的工作,每人做各项工作所消耗的时间如下表所示,问应如何指派工作,才能使总的消耗时间为最少。
若用0-1整数规划问题的常规思路来解,即:
解:令 xij = 1(第 i人完成第j项工作)或0(第 i人不进行第j项工作).于是得到一个0–1整数规划问题
Min z=15X11+18X12+21X13+24X14+19X21+23X22+22X23+18X24+26*X31
+17X32+16X33+19X34+19X41 +21X42+23X43+17*X44
使得:
Xij只能取0或者1,i,j = 1,2,3,4
最终变成一个线性规划的问题,最终将有4个x的值为1,其对应的下标便是最终的指派。
2、指派问题一般形式
设有 n 个资源(人或机器等)A1, A2, …, An,分配做 n 件事B1, B2, … Bn,要求每件事必须使用1个资源,且不同事件由不同资源完成。已知 Ai 做 Bj的效率(如劳动工时、成本、创造价值等)为cij 。问如何进行指派可使总工作效率最佳?
其中我们称Cij为效率矩阵,问题数学模型为:
3、匈牙利解法相关概念与证明
| 几个基础概念 | 解答 |
|---|---|
| 提出者及时间 | 1955年,库恩(W.W.Kuhn)利用匈牙利数学家康尼格(D.König)关于矩阵中独立零元素定理,提出了一种指派问题算法,被称为匈牙利解法。 |
| 定理1 | 设 C=(cij)是一个效率矩阵,若可行解x*=(xij)的 n个1所对应的 n个 C=(cij)均为0,则x* 是最优解。(若都为零,最终代价为0,定为最优) |
| 定理2 | 设给定了以 C=(cij)为效率矩阵的指派问题 G,现将 C的元素cij 改变为: c ′ ( i j ) = c ( i j ) − a i − b i ; a i 与 b i 为 常 数 c'(ij)=c(ij)-a_i-b_i;a_i与b_i为常数 c′(ij)=c(ij)−ai−bi;ai与bi为常数则C’=c’ij为效率矩阵的指派问题G’与G有相同的最优解 |
定理1与2则为匈牙利法的根基所在,他通过一定的操作将效率矩阵的部分元素化为0,如果存在一组0,这组0满足:1、0的个数等于矩阵的阶数(即等于任务数);2、这组0中任意两个0不同行不同列;那么这组0所对应的分配方式即为最优解
证明过程如下:
个人理解:按照指派问题的定义,在效率矩阵中每行每列都有且仅有一个数,他相对于其他数小,则最终所耗最小
这里给一个简单的例子:
例:效率矩阵 C = [ 2 3 5 7 3 5 2 8 9 5 7 8 2 2 3 9









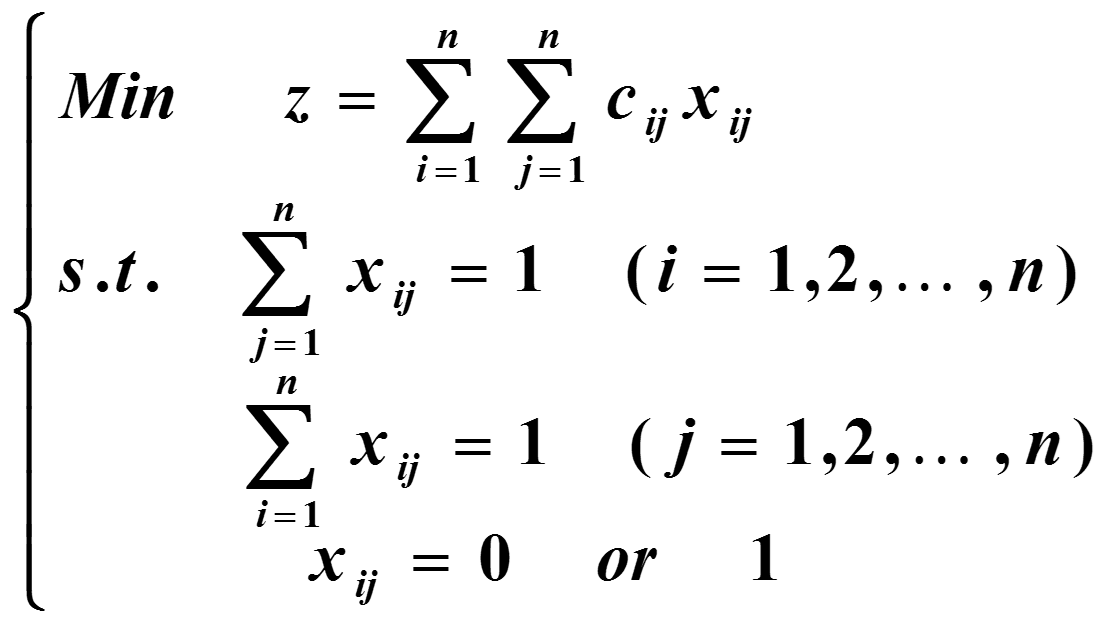
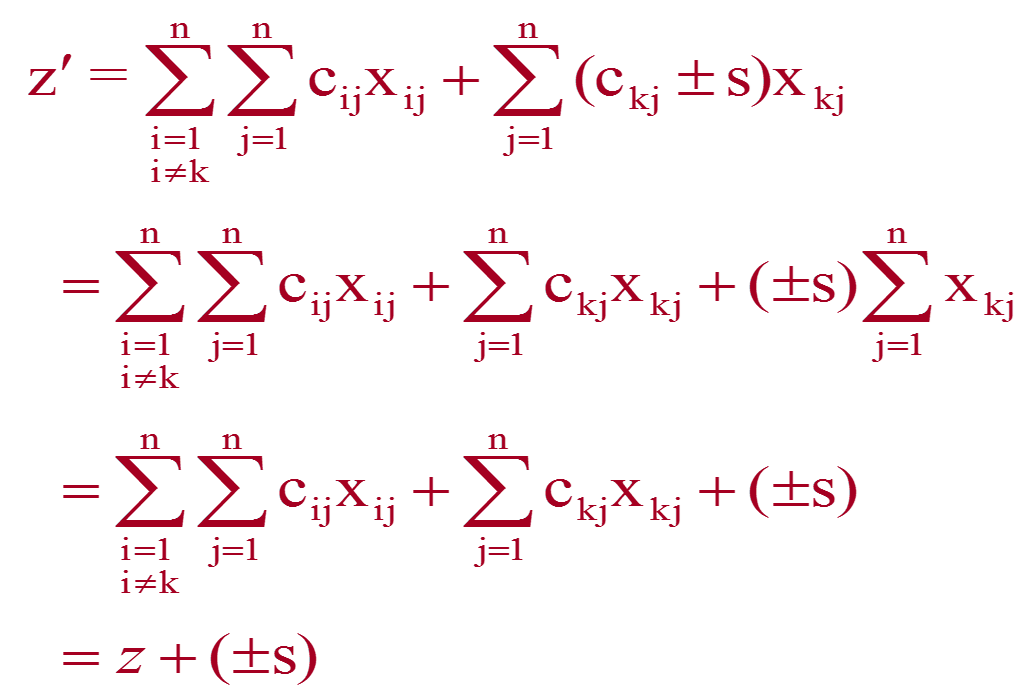
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 2232
2232

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








