Paxos算法是莱斯利·兰伯特(英语:Leslie Lamport,LaTeX中的「La」)于1990年提出的一种基于消息传递且具有高度容错特性的一致性算法。
Paxos算法一开始非常难以理解,但是一旦理解其实也并不难,之所以难理解其实是因为作者讲的故事难理解。
Paxos算法维基百科https://en.wikipedia.org/wiki/Paxos_(computer_science)
网上有2篇帖子是讲的非常好的,
分别是:以两军问题为背景来演绎Basic Paxos和Paxos算法细节详解(一)--通过现实世界描述算法
本人是在看了这2个帖子之后再结合原论文才看懂的。
Paxos一共4个角色:Client Proposer Acceptor Learner。
Client:产生议题者
Proposer :提议者
Acceptor:决策者
Learner:最终决策学习者,也就是执行者。
Proposer拿着Client的议题去向Acceptor提议,让Acceptor来决策。
Proposer提出议题,Acceptor初步接受或者Acceptor初步不接受。
Acceptor初步接受则Proposer再次向Acceptor确认是否最终接受。
Acceptor最终接受或者Acceptor最终不接受。
Learner最终学习的目标是向所有Acceptor学习,如果有多数派个Acceptor最终接受了某提议,那就得到了最终的结果,算法的目的就达到了。
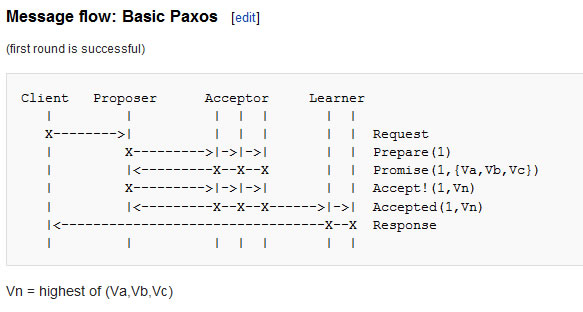
最基本的Message flow: Basic Paxos演示图如下图所示,其他情况可以参考百科。
图解:
A1,,A2和A3就是Acceptor。
P1,p2和p3就是Proposer。浅色的P1和P2说明是进行提议,深色的P1和P2说明是拿到表决。
圆圈123表明是每次提议序号,递增即可。黑色的图表示被黑了,也就是否决。方块表示投票结果,绿方块表示投票通过,红色菱形表示最终的投票结果。
整个事件是按照时间线从左到右发展。
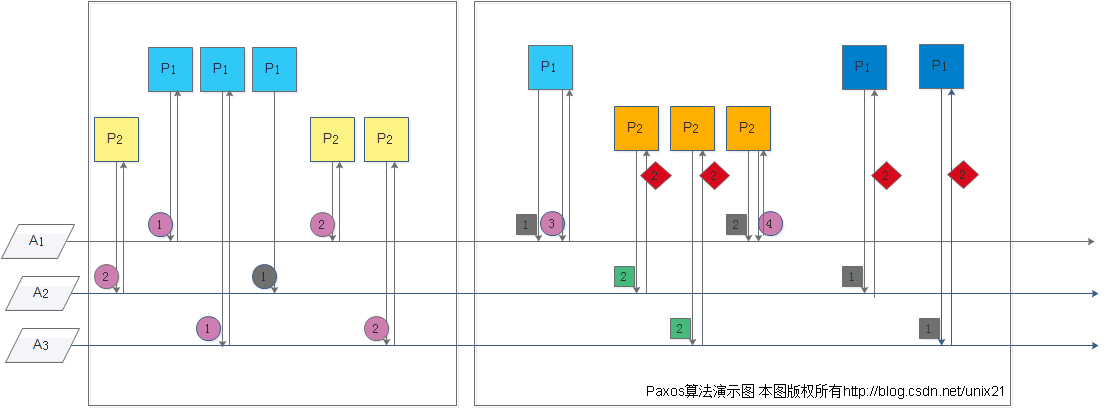
事件发展:
第一个框代表第一阶段--提议
1.p2最先找到A2,P2提议序号是2,A2记录下,因为之前没有其他的序号所以成功了,然后返回标志给p2;
2.p1找到A1,P1提议序号是1,A1记录下,因为之前没有其他的序号所以成功了,然后返回标志给p1;
3.p1找到A3,P1提议序号是1,A3记录下,因为之前没有其他的序号所以成功了,然后返回标志给p1;
问题来了
4.p1找到A2,P1提议序号是1,A2已经记录下提议序号2,2>1,所以不成功;
5.p2找到A1,P2提议序号是2,A1已经记录下提议序号1,1>2,所以成功;,然后返回标志给p2;
6.p2找到A3,P2提议序号是2,A3已经记录下提议序号1,1>2,所以成功;,然后返回标志给p2;
第二个框代表第二阶段--确认提议(投票)
7.p1找到A1,P1确认序号是1,A1已经记录下提议序号2,1<2,所以不确认,然后p1继续提议序号是3,周而复始...;
8.p2找到A2,P2确认序号是2,A2已经记录下提议序号2,2=2,所以确认成功;,然后返回投票标志给p2;
9.p2找到A3,P2确认序号是2,A3已经记录下提议序号2,2=2,所以确认成功;,然后返回投票标志给p2;
问题来了
11.p1找到A2,P1确认序号是1,A1已经记录下确认序号2,1<2,所以不确认,然后返回确认序号2;
12.p1找到A3,P1确认序号是1,A3已经记录下确认序号2,1<2,所以不确认,然后返回确认序号2;
13.p1和p2都得到确认也就是投票结果是2。14.所有的Learner最终学习的目标是2。
Paxos过程结束了,这样,一致性得到了保证,算法运行到最后所有的proposer都投“2”所有的acceptor都接受这个议题,也就是说在最初的第二阶段,议题是先入为主的,谁先占了先机,后面的proposer在第一阶段就会学习到这个议题而修改自己本身的议题,才能让一致性得到保证,这就是paxos算法的一个过程。该算法就是为了追求结果的一致性。






















 588
588

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








