动态规划 ------ 背包问题

最新推荐文章于 2024-07-20 09:21:06 发布
最新推荐文章于 2024-07-20 09:21:06 发布
阅读量894 收藏 27
点赞数 20
分类专栏： AcWing算法学习 文章标签： 算法 笔记 Acwing 动态规划 背包问题
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2201_75313100/article/details/138434803
版权
本文详细介绍了01背包、完全背包、多重背包问题以及它们的二维和一维优化方法，通过实例代码展示了如何解决这些问题，强调了动态规划在处理这类经典问题中的核心作用。
摘要由CSDN通过智能技术生成

文章目录


背包问题是动态规划中非常典型的一些题，本篇文章记录总结一下在学习过程中所遇到的一些背包问题。
其实主要就是3种,01,完全,多重背包问题，这三种详细一些，认真搞懂了，剩下的就是这三种的变种了，换汤不换药？

1. 01 背包问题

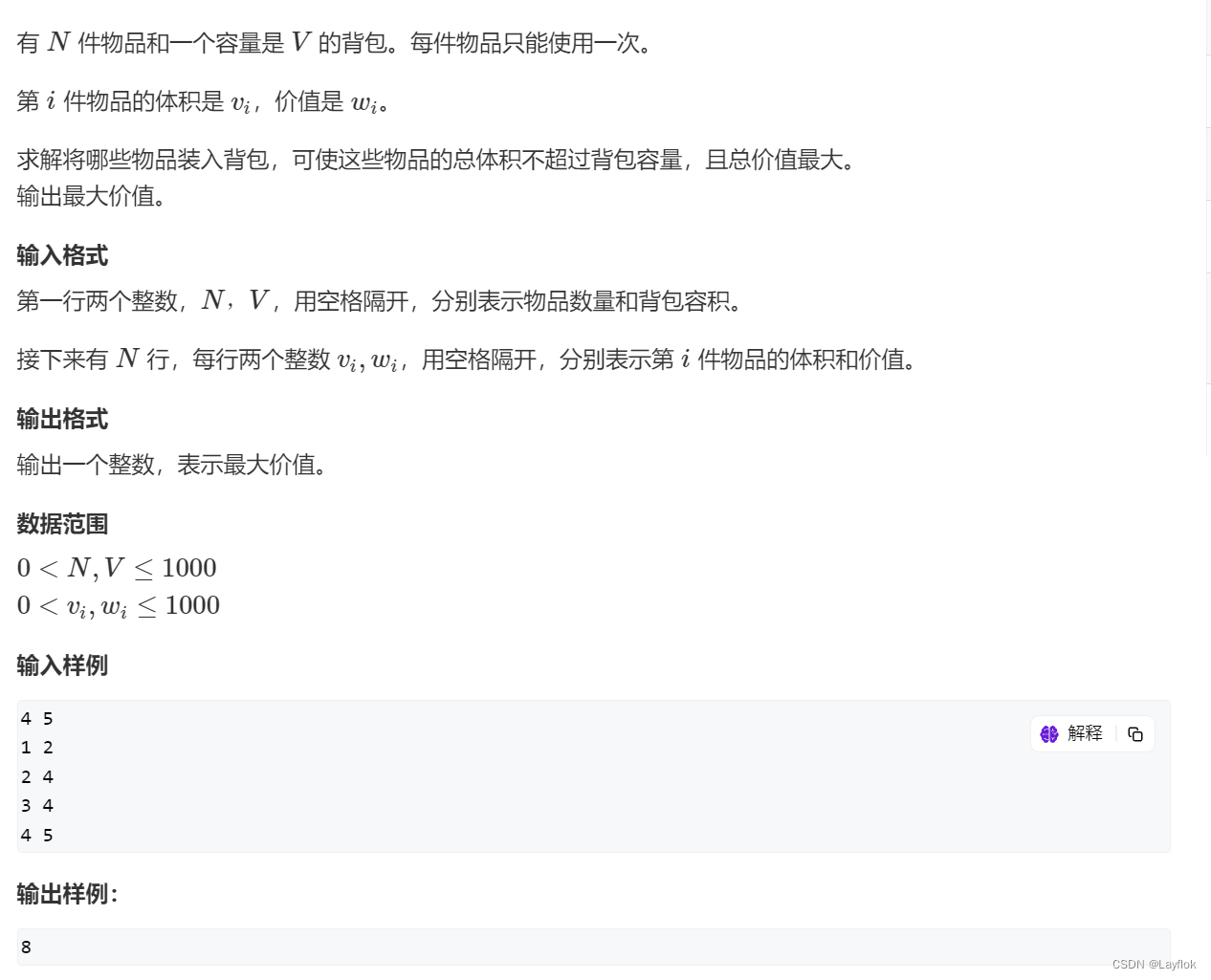
在这里插入图片描述

01背包问题链接

0 1 背包问题就是说每一件物品只能选择一次，所以我们每次选择的时候，只用两种可能，选或不选，0和1也就此而来。

1.二维解决

  • 状态表示:
  • 集合: f[i][j]代表前i件物品中体积不超过j的所有价值
  • 属性: 将所有的价值取max
  • 状态计算:
  • 对于当前的这一状态f[i][j]可以由上一个状态转移过来:
  • 0 - 不选选择当前物品 f[i][j] = f[i - 1][j].
  • 1 - 选择当前物品f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i])

不选当前物品好理解，就是去直接继承选到前一个物品时候的价值.
而选择当前物品是有条件的，就是说当前背包的容量j 必须大于等于当前的物品的体积v[i]才能选择.j - v[i]说的是当前背包的容量减去当前物品的体积，咱既然要选择这个物品，那么必须得这个物品留出相应的空间。

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N]; //v体积，w价值
int f[N][N];    //f[i][j] 表示前i件物品中体积是j的最大价值.

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d%d", &v[i], &w[i]);
    
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];
            if (j >= v[i])
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    
    printf("%d\n", f[n][m]);
    return 0;
}

2. 一维优化

我们还可以对其进行进行优化，可以讲二维优化成一维。
f[i]表示体积是i时候的最大价值.

  1. f[i][j] = f[i - 1][j] 变成 f[j] = f[j] 所以可以直接不写
  2. f[i - 1][j - v[i]] 变成f[j - v[i]]但是此变形并不是等价的，因为我们在真正循环的过程中其实是用f[i][j - v[i]] 于前面的不符，需要将其进行逆序。

大家也可看看这这一篇题解

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N]; //v体积，w价值
int f[N];    //f[i][j] 表示前i件物品中体积是j的最大价值.

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d%d", &v[i], &w[i]);
    
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--)
                f[j] = max(f[j], f[j - v[i]] + w[i]);
    
    printf("%d\n", f[m]);
    return 0;
}

2. 完全背包问题

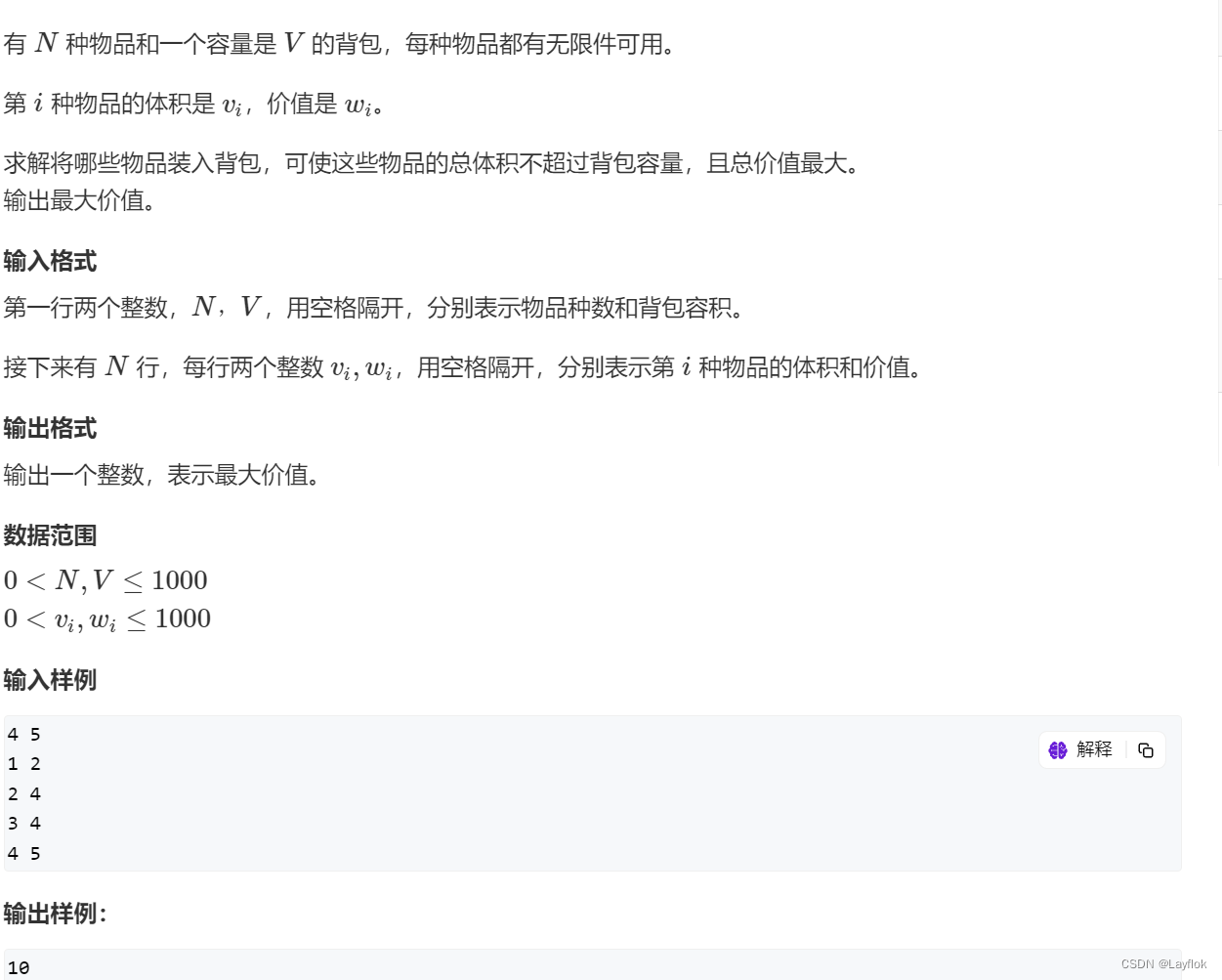
在这里插入图片描述

完全背包问题链接

完全背包问题和01背包问题唯一的区别就是，完全背包中的物品可以使用无限次，
而01背包中的物品只能使用一次。

1.暴力3 for.

  • 状态表示:
  • 集合: f[i][j]表示背包容量是i中所选体积不超过j的所有价值
  • 属性: 对所有的价值取max
  • 状态计算:
  • 因为每一个物品可以选择无限次,前提是满足背包容量.
我们尝试用一个变量 k 来充当第i个物品选取k次，
那么k的范围则是 [0,k] 但是k必须满足 k * v[i] <= j. 
因为选取的体积不能超过背包的总容量。
即： f[i][j] = max(f[i][j],f[i - 1][j - k * v[i]] + k * w[i]);
  • 可以发现上面的方程和01背包问题一摸一样，只是多了一个k而已。如果不理解，将k = 1代入即使01背包问题的动态转移方程。而不选的时候则k = 0.
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d%d", &v[i], &w[i]);
    
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
            for (int k = 0; k * v[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
    
    printf("%d\n", f[n][m]);
    return 0;
}

这道题目用这个代码是会超时的，但是思路肯定是对的，理解思路才能理解下面的优化。

2. 二维优化

我们将上述的动态转移方程展开

2v = 2 * v && 2w = 2 * w;
f[i][j] = max(f[i-1][j-0v],f[i-1][j-v]+w,f[i-1][j-2v]+2w,f[i - 1][3v]+3w,...)
f[i][j-v] = max(f[i-1][j-v-0v]+0w,f[i-1][j-v-v]+w,f[i-1][j-2v]+2w+....)

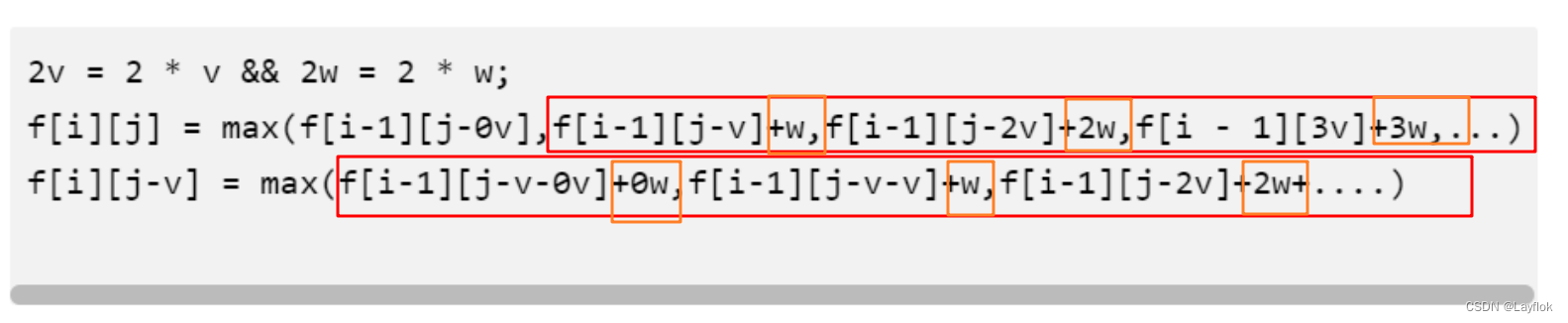
在这里插入图片描述
我们可以发现，f[i][j]展开的这一大堆于f[i][j - v]展开的这一大堆是仅仅相差一个w。
所以:
f[i][j] = max(f[i - 1][j], f[i][j - v] + w).

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d%d", &v[i], &w[i]);
    
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];
            if (j >= v[i])
                f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }
    
    printf("%d\n", f[n][m]);
    return 0;
}

这个代码于01背包问题二维进仅仅差1个数字.
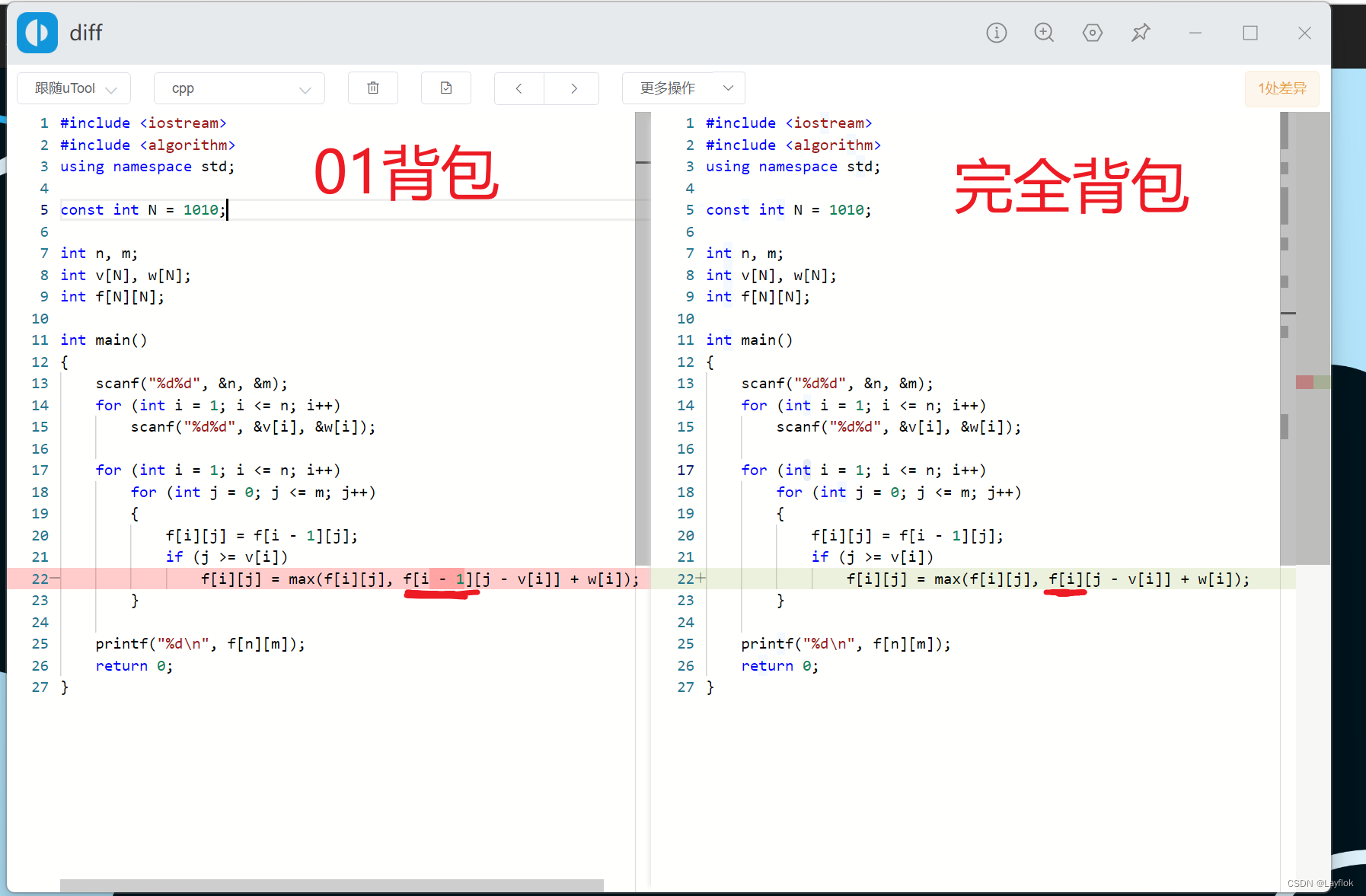
在这里插入图片描述

3. 一维优化

既然只差那一个数字，所以完全背包也可以将其进行优化成一维的。
我们之间在优化01背包的时候提到过：

  • f[i][j] = f[i- 1][j] 转化成f[j] = f[j]直接可以省略掉。
  • 而01背包因为f[i - 1][j - v[i]] 转化成f[j]因为是i - 1所以需要逆序体积遍历。
  • 在完全背包中f[i][j - v[i]]转化成f[j]因为是i所以不需要进行逆序。
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d%d", &v[i], &w[i]);
    
    for (int i = 1; i <= n; i++)
        for (int j = v[i]; j <= m; j++)
                f[j] = max(f[j], f[j - v[i]] + w[i]);
    
    printf("%d\n", f[m]);
    return 0;
}

3. 多重背包问题Ⅰ.

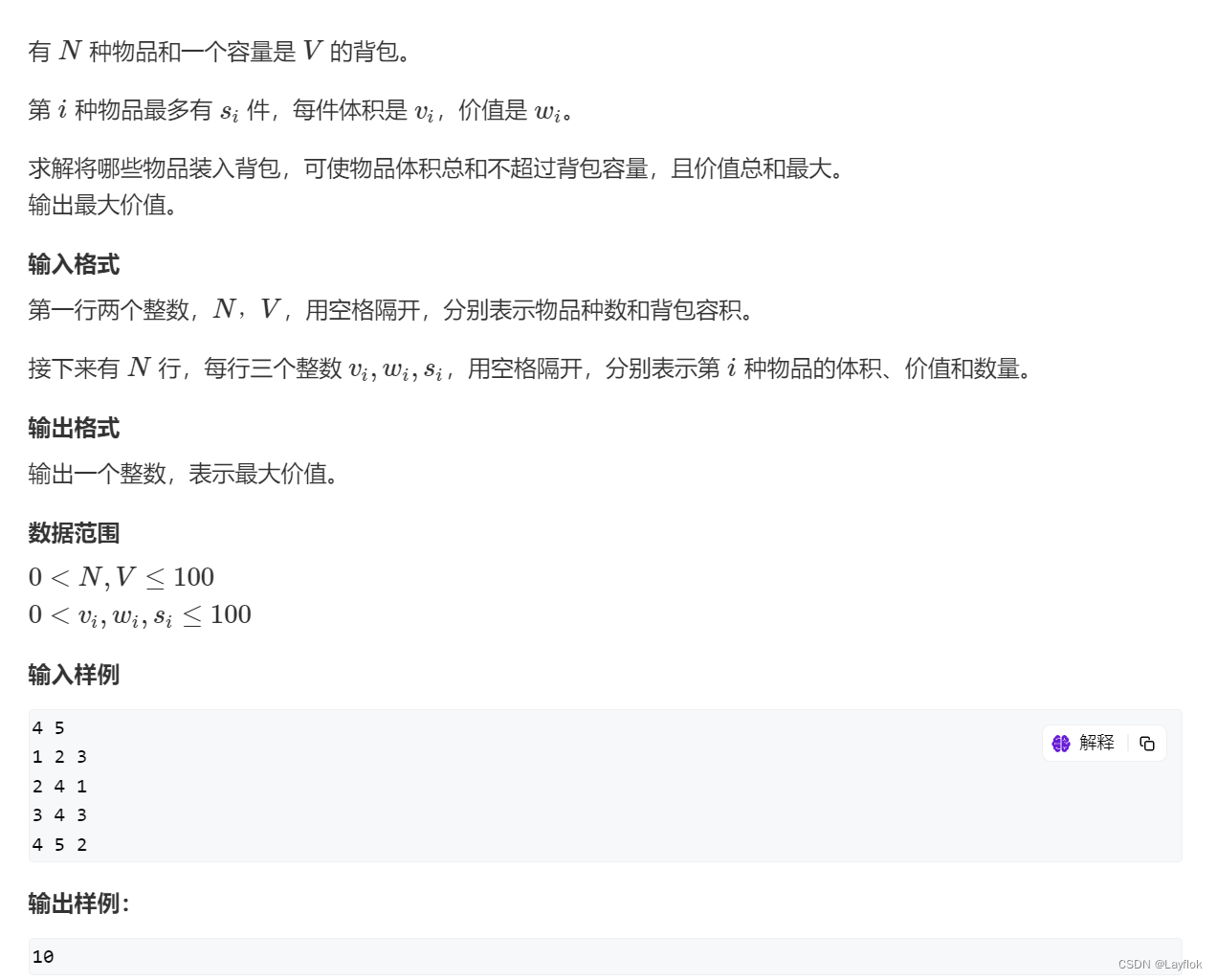
在这里插入图片描述

多重背包问题Ⅰ链接

多重背包问题是将物品的个数做了限制，在给定的这些物品中，选择总价值不超过所给背包体积的最大总价值。

1. 二维解决

我们在上面的完全背包问题中已经学会了0~k次的选择一个物品，至于k的范围则是使k * v[i] <= j将其最大化。而本题中则可以直接获取。
前两种背包问题真的搞懂之后，这道题只需要加一个条件即可。
在这里插入图片描述

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int f[N][N];
int v[N], w[N], cnt[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d%d%d", &v[i], &w[i], &cnt[i]);
    
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
            for (int k = 0; k <= cnt[i] && k * v[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
    printf("%d\n", f[n][m]);
    return 0;
}

2. 一维优化

同之前的优化一样，直接去掉一个维度。
他是01背包问题的变种，删除前是i - 1与删除后并不是等价的，所以需要逆序。

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int f[N];
int v[N], w[N], cnt[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d%d%d", &v[i], &w[i], &cnt[i]);
    
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--)
            for (int k = 0; k <= cnt[i] && k * v[i] <= j; k++)
                f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);
    printf("%d\n", f[m]);
    return 0;
}

4. 多重背包问题Ⅱ

多重背包问题Ⅱ链接
这个问题与上方的区别只是数据范围变了，之所以单独拿出来，是因为，这里涉及到了一个二进制的优化，感觉还是挺重要的。
我们假设去店里面送水果，有13颗苹果，16颗梨，11颗西瓜。需要讲这40个水果搬如店中，我们如果一个一个搬，需要40次，说实话有点捞。。。但凡是个正常人我们都应该讲其分开搬，具体怎么分呢，我们采取二进制的方式将其分开。
1,2,4,8,16,32........等等这样一直分下去，但前提一定得是一样的物品分一起，不然你的体积和价值如何计算？
上述例子：
苹果: 1, 2 ,4, 7.
梨: 1, 2, 4, 8, 1.
西瓜: 1, 2, 4, 4.
我只是举个例子，现实生活中肯定不是二进制的搬，1个苹果占一个箱子？
下面的代码就是向上述例子一样，将其一类一类的分组打包。
然后就会变成了01背包问题。

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 1e5 + 10, M = 2010;

int n, m;
int v[N], w[N];
int f[M];

int main()
{
    scanf("%d%d", &n, &m);
    int cnt = 0;	//从1开始放。
    for (int i = 1; i <= n; i++)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        int k = 1;
        
        while (k <= c)
        {
            v[++cnt] = a * k;	//先++。
            w[cnt] = b * k;
            
            c -= k;
            k *= 2;
        }
        
        if (c > 0)
        {
            v[++cnt] = a * c;
            w[cnt] = b * c;
        }
    }
    
    n = cnt;
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
            
    printf("%d\n", f[m]);
    
    return 0;
}

5. 混合背包问题

在这里插入图片描述

混合背包问题链接

混合背包问题就是讲前面所说的3中背包混合在一起。
我们既然已经会了前三种的状态转移方程，那么我们只需要在做的时候，对其进行套用相应的方程即可。
又因为多重背包问题可以将其进行二进制优化转化为01背包问题，所以我们只需要对其进行2个方程各自对应即可。
总的来说也就2个步骤

  • 将多重背包利用二进制优化转化为01背包
  • 将01背包与完全背包各自动态转移方程代入即可。
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;

const int N = 1010;

int n, m;
int f[N];
struct Thing
{
    int kind;
    int v, w;
};
vector<Thing> things;


int main()
{
    scanf("%d%d", &n, &m);
    //第一步:将多重背包利用二进制优化转化为01背包
    for (int i = 1; i <= n; i++)
    {
        int v, w, s;
        scanf("%d%d%d", &v, &w, &s);
        if (s <= 0) //01背包或者完全背包直接插入即可。
            things.push_back({s, v, w});
        else
        {
            //多重背包进行二进制优化，分包
            for (int k = 1; k <= s; k *= 2)
            {
                s -= k;
                things.push_back({-1, v * k, w * k});
            }
            
            if (s > 0)
                things.push_back({-1, v * s, w * s});
        }
    }
   	//第二步:将01背包与完全背包各自动态转移方程代入即可。
    for (auto t : things)
    {
        if (t.kind == -1)   //01背包的动态转移方程
            for (int j = m; j >= t.v; j--)
                f[j] = max(f[j], f[j - t.v] + t.w);
        else                //完全背包的动态转移方程
            for (int j = t.v; j <= m; j++)
                f[j] = max(f[j], f[j - t.v] + t.w);
    }
    
    printf("%d\n", f[m]);
    return 0;
}

6. 二维费用背包问题

在这里插入图片描述

二维费用背包问题链接

二维费用，只是多了一个书包的承受范围，只需要在01背包的基础上多加一层关于重量的的循环就好了。

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n, V, M;            //个数，容积， 承受范围
int v[N], m[N], w[N];   //体积，重量，价值
int f[N][N];            //f[i][j]表示容积不超过i，重量不超过j的最大价值

int main()
{
    scanf("%d%d%d", &n, &V, &M);
    
    for (int i = 1; i <= n; i++)
        scanf("%d%d%d", &v[i], &m[i], &w[i]);
    
    for (int i = 1; i <= n; i++)
        for (int j = V; j >= v[i]; j--)         //容积
            for (int k = M; k >= m[i]; k--)     //承受范围
                f[j][k] = max(f[j][k], f[j - v[i]][k - m[i]] + w[i]);
    
    printf("%d\n", f[V][M]);
    return 0;
}

7. 分组背包问题

在这里插入图片描述

分组背包问题链接

分组背包问题，其实归根结底还是01背包问题，每组只能选择一个物品出来，只不过这一组有很多个物品。
所以我们针对其每一组，将其所有的物品都遍历一遍就好了，在01背包问题上再加一层循环，3for就好了。
01背包问题，同样还是逆序，不过判断j >= v[i]的条件变成了j >= v[k]了。

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 110;

int n, m;
int f[N], v[N], w[N];

int main()
{
    scanf("%d%d", &n, &m);
    
    for (int i = 1; i <= n; i++)
    {
        int s;
        scanf("%d", &s);
        for (int j = 1; j <= s; j++)
            scanf("%d%d", &v[j], &w[j]);
        
        for (int j = m; j >= 0; j--)
            for (int k = 1; k <= s; k++)
                if (j >= v[k])
                    f[j] = max(f[j], f[j - v[k]] + w[k]);
        
    }
    printf("%d\n", f[m]);
    return 0;
}

🎈🎈🎈🎈🎈🎈🎈🎈🎈🎈🎈🎈🎈🎈

Layflok
关注
  • 20
    点赞
  • 踩
  • 27
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
动态规划-01背包问题
11-16
01背包问题是一种经典的计算机科学优化问题，主要应用于资源分配、任务调度等领域，它通过动态规划的方法求解最优解。动态规划是一种解决复杂问题的有效算法，通过将问题分解为更小的子问题，并存储子问题的解以避免...
动态规划-背包问题1
08-03
0-1背包问题是一个经典的动态规划应用实例，它属于整数规划的范畴。在这个问题中，我们有一个容量有限的背包，需要从一系列物品中选择，每个物品都有自己的重量和价值，目标是使得背包内物品的总价值最大，但总重量...
动态规划-背包问题详解
2203_75327677的博客
01-19 1311
基于动态规划，对背包问题的四种情况进行详解
动态规划-背包问题
qwertyasdfghh的博客
01-08 1149
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i]。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是o(2^n)，这里的n表示物品数量。所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化！思路：本体如何化为背包问题是解题的关键和难点，这里我试想过用一个背包装2个元素这样的思路来想，想了半天都想不通，
动态规划-- 背包问题
qq_48094059的博客
07-18 2970
动态规划--背包问题
动态规划------背包问题详解
weixin_45102820的博客
08-05 3982
一、01背包 有n件物品，每件物品占用的空间为w[i], 价值为p[i]。 有容量为 V 的背包。求在容量允许的范围下，背包装入物品的最大价值。 在当前为i，v的情况下，考察第i件物品。有两种情况。 1、如果i物品的体积大于v，装不下了。就只能放弃。则最大价值不变。dp[i][v] = dp[i-1][v]; 2、如果i物品的体积不大于v，可以选择装入i或者放弃i。 如果装入i，则剩余的容量变为v-w[i]。整个问题变为，先把i装入，再用v-w[i]的空间去装前i-1件物品。 dp[i][v] = dp[i
动态规划--背包问题
qq_45756062的博客
10-19 1012
可以放入背包的物品有n种,每种物品的重量和价值分别为wi, vi如果背包的最大重量限制是b,每种物品可以放多个.怎样选择放入背包的物品以使得背包的价值最大?所以Fk(y) = max{ Fk-1(y)，Fk(y-nwk) + nvk } n是装入第k个物品的数量。递推方程F(k,b,v) = F(k-1,b-nbk,v-nvk) + nVk（值n倍的第k个物品的价值）s[k] [y] = 装入前k个物品最大限重y时，最大价值时，装入的第k个物品的数量。当k=0是，所有的F0(y)都等于0；
Java学习之动态规划-背包问题代码
05-16
在编程领域，动态规划是一种强大的算法，常用于解决复杂的问题，比如背包问题。本文将深入探讨Java中的动态规划实现，特别是在解决背包问题时的应用。背包问题是一个经典的优化问题，它通常涉及在一个容量有限的背包...
动态规划-0-1背包问题
06-12
动态规划是一种重要的算法思想，...0-1背包问题的动态规划解法不仅展示了这一思想，同时也为我们提供了处理类似最优化问题的一个通用框架。通过深入学习和实践，我们可以掌握动态规划的精髓，从而更好地解决实际问题。
源代码_背包问题--01背包_
10-02
01背包问题是一种经典的计算机科学中的动态规划问题，主要出现在算法设计和优化的领域，尤其在求解资源分配和组合优化问题时非常常见。在这个问题中，我们有一个背包，其容量有限，同时有一系列物品，每种物品都有...
Held-Karp算法的C++代码
m0_61862494的博客
07-19 113
Held-Karp算法是动态规划的一种应用，用于解决旅行商问题 (TSP)。该算法通过记录部分路径的最小成本来避免重复计算，从而有效地降低计算复杂度。Held-Karp算法使用一个状态压缩动态规划表。表示从起点出发，访问过所有由。表示的集合中的节点，并以节点。结束的最小路径长度。
Leetcode—207. 课程表【中等】
Atticus的博客
07-19 239
运行结果 之后我会持续更新，如果喜欢我的文章，请记得一键三连哦，点赞关注收藏，你的每一个赞每一份关注每一次收藏都将是我前进路上的无限动力 ！！！↖(▔▽▔)↗感谢支持！
代码随想录学习 54day 图论 A star算法
qq_40445763的博客
07-17 467
【代码】代码随想录学习 54day 图论 A star算法。
插入和选择排序
最新发布
c23856的博客
07-20 211
我们来计算一下它的时间复杂度：我们知道时间复杂度是计算最坏的情况，在这里的最坏情况为逆序，因为逆序的时候每次插入都需要执行前面数的数量，那么我们假设其有N个数，那么总执行量就为：1+2+3...+N-1 即为(N^2)/2。时间复杂度：O(N*logN),我们设该树高为h，那么树的所有节点为N=2^h-1个，我们的时间复杂度要换成与数量有关的式子，所以时间复杂度为O(N*logN).希尔排序是在插入排序的基础上，效率更高的排序，其实就是在插入排序的基础上加上了与预排序的操作。
【JavaScript 算法】栈与队列：解决括号匹配问题
Allen-
07-17 566
在编程中，括号匹配问题是一类常见的算法题，通常用于验证括号的正确性，即检查括号是否成对出现且嵌套正确。栈（Stack）是一种非常适合解决括号匹配问题的数据结构。本文将详细介绍如何使用栈来解决括号匹配问题的原理、实现及其应用。
完全二叉树的节点个数-递归
qq_45031559的博客
07-19 219
完全二叉树的节点个数-递归
【java】力扣 H指数
qq_55846232的博客
07-17 286
java 力扣 H指数
【算法】算法模板
qq_44765647的博客
07-19 269
LeetCode网站中学习算法的过程中使用到并总结的算法模板算法模板 数组算法模板，字符串算法模板，列表算法模板，数学算法模板，树算法模板，图算法模板，动态规划算法模板

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值