目录
背包问题总结
后期写
背包问题介绍
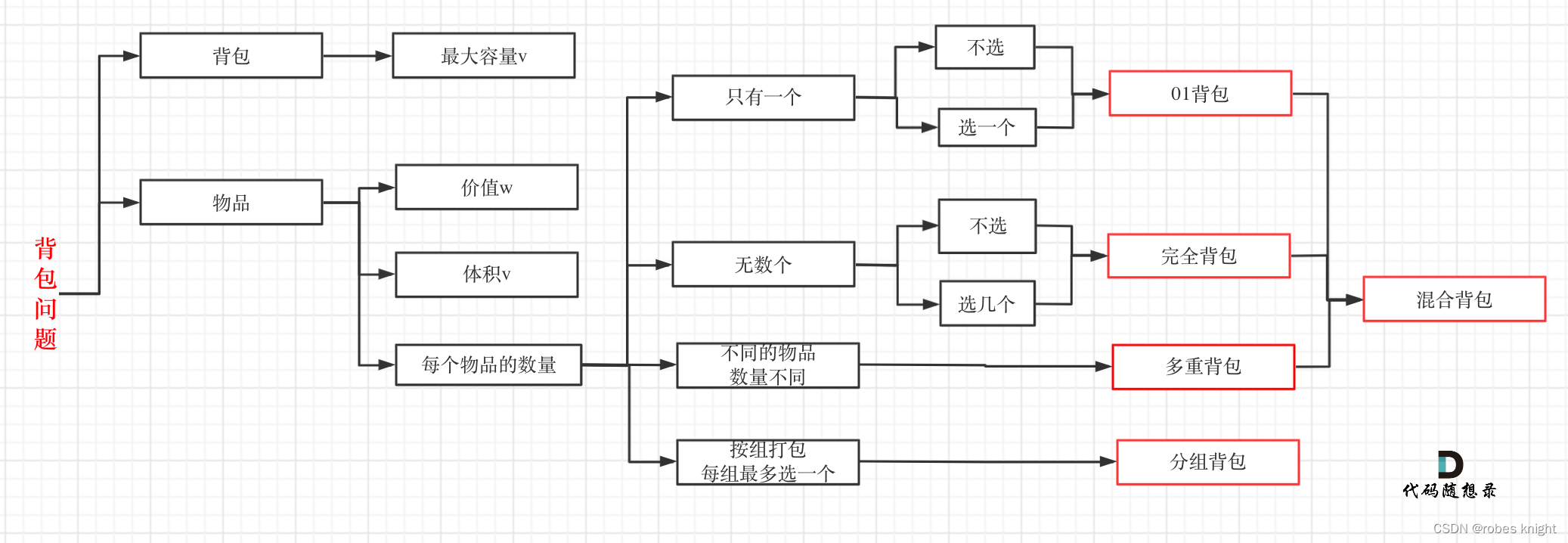
1. 01背包
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。

每一件物品其实只有两个状态,取或者不取,所以可以使用溯法搜索出所有的情况,那么时间复杂度就是o(2^n),这里的n表示物品数量。
所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化!
1.1 二维dp数组01背包
第一步要明确两点,「状态」和「选择」。
先说状态,如何才能描述一个问题局面?只要给几个物品和一个背包的容量限制,就形成了一个背包问题呀。所以状态有两个,就是「背包的容量」和「可选择的物品」。
再说选择,也很容易想到啊,对于每件物品,你能选择什么?选择就是「装进背包」或者「不装进背包」嘛。
明确状态和选择,然后就往这个框架套:
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 择优(选择1,选择2...)
(1)确定dp数组以及下标的含义
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j(总容量,不是剩余容量)的背包,价值总和最大是多少。
(2)转移方程
简单说就是,上面伪码中「把物品 i 装进背包」和「不把物品 i 装进背包」怎么用代码体现出来呢?
这就要结合对 dp 数组的定义,看看这两种选择会对状态产生什么影响:
如果你没有把这第 i 个物品装入背包,
那么很显然,最大价值 dp[i][j] 应该等于 dp[i-1][j],继承之前的结果。
如果你把这第 i 个物品装入了背包,
那么 dp[i][w] 应该等于 val[i-1] + dp[i-1][j - weight[i]]。
一方面,选择将第 i 个物品装进背包,那么第 i 个物品的价值 val[i-1] 肯定就到手了
另一方面,我们相当于将第i个物品和weight[i]抵消,继承dp[i-1][j - weight[i]]的值
因此转移方程:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); (3)初始化!!!重要
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
j是由左边的更小的j推出来的,因此,最左边一列也要初始化啊
第一列:dp[i][0]
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
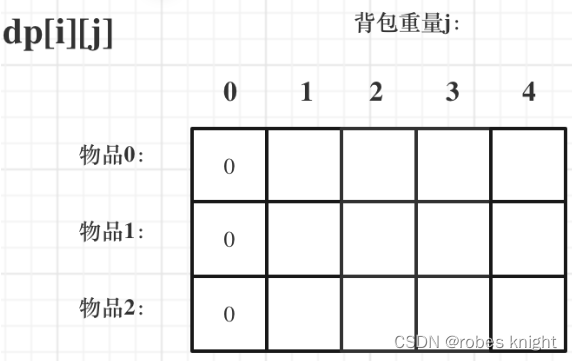
第一行:dp[0][j]
即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品,因此只需要把大于weight[0]的j都初始化为value[0]就行
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}其他位置不需要初始化,都会被覆盖,因此方便起见,设置为0

代码:
// 初始化 dp
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}(4)遍历顺序-后续补充
基础的01背包比较简单,但是后续遇到了比较复杂的背包,不同遍历顺序是有区别的
先看这个问题,有两个遍历的维度:物品与背包重量,
那么问题来了,先遍历 物品还是先遍历背包重量呢?
其实都可以!! 但是先遍历物品更好理解。
因为由转移方程可知,dp[i][j]由左上角决定,对于两种顺序,有用的初值都在左上角,所以没有区别
(5)打印检查
检查一下
完整代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int main(){
int n,v;
cin>>n>>v;
vector<int> value(n+1,0);
vector<int> weight(n+1,0);
int m = 0;
for(int i = 1; i <= n; i++){
cin>>weight[i]>>value[i];
}
vector<vector<int>> dp(n+1,vector<int>(v+1,0));
for(int j = 0;j < v;j++){
if(j > value[0])dp[0][j] = value[0];
}
for(int i = 1;i <= n; i++){
for(int j = 1;j <= v; j++){
if(j < weight[i])
dp[i][j] = dp[i-1][j];
else
dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]] + value[i]);
}
}
cout<<dp[n][v];
return 0;
}(注意:)关于下标起始为0还是1的解释:
遍历dp时是从1开始遍历,这是因为i=0和j=0都已经初始化过了,我们认为i=0表示没有装物品,j=0表示体积为0,那么存放weight和volume的数组的下标必须从1开始,这样weight[i]能表示第i个物品(而不是i+1),weight[0]也有意义了
1.2 一维dp01背包-滚动数组-状态压缩
我们之前在做其他一维dp的题时,发现如果dp[i]只和dp[i-1]有关,那么我们就可以使用两个变量来压缩dp数组,从而降低空间复杂度
再回顾二维dp解01背包,转移方程为:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 为了更加直观,我们使用图片解释: 以图中的8为例,我们发现当前点的状态只和上一行dp[i-1]有关,根据转移方程,我们发现,每一个点dp[i][j]都只和上一行有关
以图中的8为例,我们发现当前点的状态只和上一行dp[i-1]有关,根据转移方程,我们发现,每一个点dp[i][j]都只和上一行有关
因此,我们可以将二维数组压缩为一维,如下图:
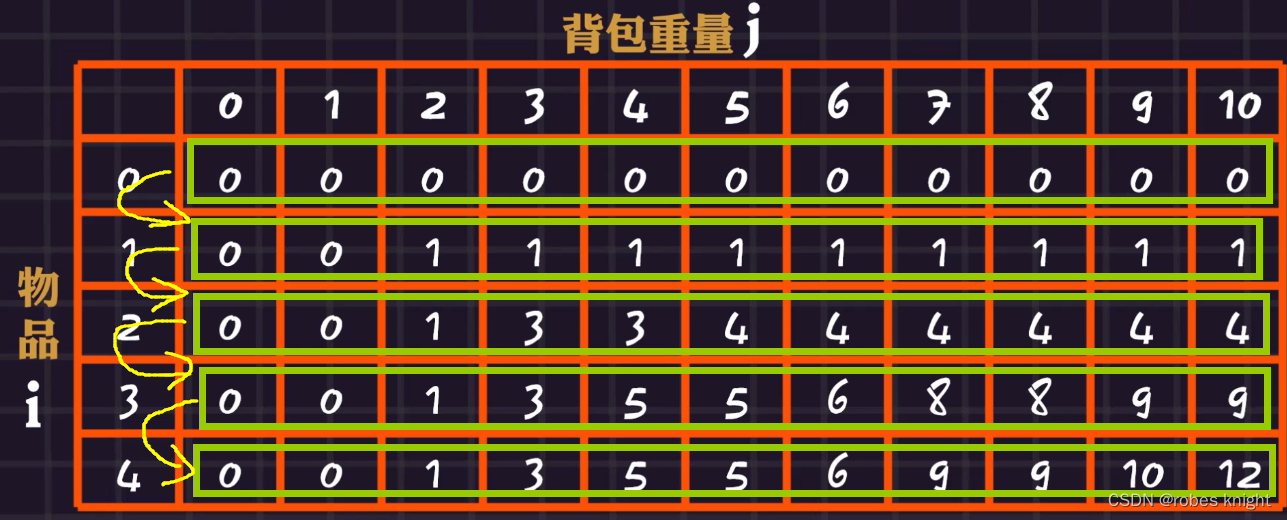
每次的dp数组只保留一行的数据,同时因为dp[i][j]依靠的是上一行左边的值,那么也就是说我们更新当前值之前,左边的数不能更改,所以选择从右往左遍历
整体流程:每次遍历完一遍之后,当前dp[j]中已经存满了上一行的状态,然后我们为了防止数据被破坏,从右往左将上一行的数据,更新为这一行的数据,然后准备进行下一层遍历
(1)dp定义:
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
(2)转移方程:
根据定义,我们当前的dp[i]取决于原有的dp[i]和dp[j - weight[i]] + value[i],所以转移方程为:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);(3)初始状态
其实本质上这里的初始化和二维的初始化没有任何区别,但一维最开始只有一行,所以我们只需要将二维dp的初始化中的第一行用来初始化一维dp即可
(4)遍历顺序:
因为我们是一行一行(一个个物品递增)的更新,且每次都需要填满所有背包,那么就应该外层是物品,内层是背包,将递增的物品放到每一个背包
而且,我们每一行都是从后往前遍历,因此背包要从后往前遍历
注意,二维dp中还有一个情况就是weight[i] > j,物品i放不进背包,就继承正上方的值,在此处,正上方的值正好就是上一轮dp[i]的值,那么对于这些放不进去的背包,不更新即可
也即是从最大背包往前遍历到weight[i]就可以了
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) // 遍历背包容量(5)打印检查
走个流程
因此,完整代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int main(){
int n,v;
cin>>n>>v;
vector<int> value(n+1,0);
vector<int> weight(n+1,0);
int m = 0;
for(int i = 1; i <= n; i++){
cin>>weight[i]>>value[i];
}
// vector<vector<int>> dp(n+1,vector<int>(v+1,0));
// for(int j = 0;j < v;j++){
// if(j > weight[0])dp[0][j] = value[0];
// }
// for(int i = 1;i <= n; i++){
// for(int j = 1;j <= v; j++){
// if(j < weight[i])
// dp[i][j] = dp[i-1][j];
// else
// dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]] + value[i]);
// }
// }
// cout<<dp[n][v];
vector<int> dp(v+1,0);
for(int j = 0;j < v;j++){
if(j > weight[0])dp[j] = value[0];
}
for(int i = 1;i <= n;i++){
for(int j = v; j >= weight[i];j--){
dp[j] = max(dp[j],dp[j - weight[i]] + value[i]);
}
}
cout<<dp[v];
return 0;
}1.3 01背包相关题目
1.3.1 分割等和子集

先计算总和sum,然后用一个sum/2大小的背包来放nums的元素,放完了检查剩下的值是否和放进去的值相等
因此定义dp:
容量为j的背包,放入数的和为dp[j] (相当于将nums[i]本身的值当作了value[i])
其他部分和一维01背包一样,代码如下:
class Solution {
public:
bool canPartition(vector<int>& nums) {
int n = nums.size(),sum=0,subsum;
for(int i = 0;i < n;i++)
sum+=nums[i];
if(sum%2 == 1)return false;
else subsum = sum/2;
vector<int> dp(subsum+1,0);
for(int i = 0;i < n;i++)
for(int j = subsum;j >= nums[i];j--)
dp[j] = max(dp[j],dp[j-nums[i]]+nums[i]);
return dp[subsum] == (sum - dp[subsum]);
}
};1.3.2 最后一块石头的重量
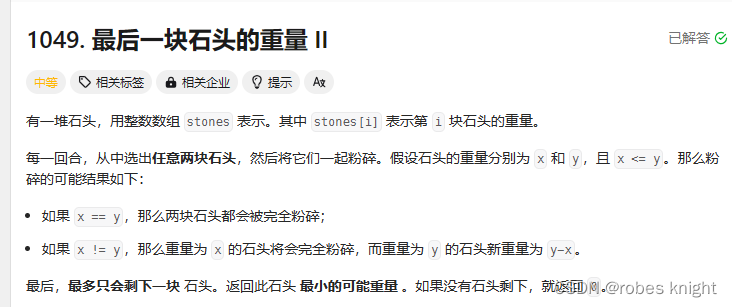
思路:
本体如何化为背包问题是解题的关键和难点,这里我试想过用一个背包装2个元素这样的思路来想,想了半天都想不通,所以背包问题难的不是怎么写背包,是怎么看出来是背包问题还有怎么使用背包来解题
这里说一种根据一些题总结的思路,我们一般求01背包都是先求和,然后分为两部分,一部分装进背包里,另一部分不放进背包(一部分确定了,另一部分就也确定了)
这里我们通过这样的思想进行思考:
我们可以先求和得到总重量sum,然后设置一个sum/2容量的背包,往里面尽量装满石头,也就将一堆石头尽量分为了两堆重量接近的部分,然后这两堆进行相撞就能得到结果
(1)dp定义
容量为j的背包最多能装入的石头的重量为dp[j]
(2)转移方程
通过重量进行更新:
dp[j] = max(dp[j],dp[j - stones[i]]+stones[i]);(3)初始化
如下:

(4)遍历顺序:
正常01背包顺序
完整代码如下:
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
int n =stones.size(),sum=0;
for(int i = 0;i < stones.size();i++)
sum +=stones[i];
int subsum = sum/2;
vector<int> dp(subsum+1,0);
for(int i = 0;i < n;i++)
for(int j = subsum;j >= stones[i];j--){
dp[j] = max(dp[j],dp[j - stones[i]]+stones[i]);
}
return sum - 2*dp[subsum];
}
};1.3.3 目标和-!!!求次数,方程更新方法特殊
此题和数据结构与算法-动态规划(基础框架+子序列问题)-CSDN博客
中的不同子序列一题非常像,都是求一共有多少种方案,而不是最优的一次方案
此题有点特殊,但是主要特殊在转移方程的更新,其他部分还是和一般的01背包相同
思路:
仍然是先求和然后分为两个部分进行求解,先求和,然后我们将target部分先剔除,这意味着剩下的部分要相互抵消才行,因此我们设置两部分分别为:
(sum - target)/2(减法部分) 和(sum - target)/2 + target(加法部分)
注意:这道题可以用一维dp做,但是需要二维dp的思考方式来思考,不然很难理解
(1)dp定义:
dp[j] 表示,数值和为j的背包,装满有dp[j]种方法
(2)转移方程:
这是这部分的重点:
我们回顾之前不同子序列一题的转移方程:
if(s[i-1] == t[j-1])
dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
else{
dp[i][j] = dp[i-1][j];
} 这里同理,更新的时候要分情况考虑:
1)考虑nums[i]
如果考虑的话,那么将nums[i]纳入次数统计中,按照二维dp理解(i表示使用[0,i]的物品组合),由于物品数和总和同时增加了,且每次计数都需要考虑最后这个物品nums[i],因此也就相当于只变化前[0,i-1]个物品组合,因此次数为:
dp[i-1][j-nums[i]]化为一维:
dp[j-nums[i]]2)不考虑nums[i]
不考虑nums[i],也就是每次计数都不把nums[i]纳入考虑之中,也就相当于不把其放入背包,也就相当于对容量为j的背包只考虑前[0,i-1]的组合,等于:
dp[i-1][j]化为一维:
dp[j]同时,这里是求解路径数而不是最优路径,那么我们每次选择的不同路径应该相加而不是取最优,所以方程如下:
dp[j] = dp[j]+dp[j-nums[i]];(3)初始化:
我们把空当作一个空格,没有任何属性的空格,这里空填满空有1种方式所以填1但是注意假如是在统计元素个数什么的,空不能算一个元素,因为题目中规定的元素没有包含空,在后一题一零和中要注意

(4)遍历方向:
常规
代码如下:
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int n = nums.size(),sum = 0;
for(int i = 0 ;i < n;i++)sum += nums[i];
if((sum -abs(target))%2 == 1) return 0;
int plus = abs(target) + (sum -abs(target))/2;
vector<int> dp(plus+1,0);
dp[0] =1;
for(int i = 0; i< n;i++)
for(int j = plus ;j >=nums[i];j--)
dp[j] = dp[j]+dp[j-nums[i]];
return dp[plus];
}
};1.3.4 零一和-三维dp(压缩后二维)

此题难点不在思路转换上,而是在将二维问题延申到三维上
此题有两个限制条件;m n,也即是说,我往背包里面放东西需要有两方面的限制,由此需要三维dp数组来实现
(1)dp定义:
dp[k][i][j]表示[0,k]的物品的组合,形成的集合中,0个数<=m,1个数<=n的背包中,能够容纳的最大物品数量是多少
简化为dp[i][j]二维
(2)转移方程:
注意这里的+1,表示增加一种情况
dp[k][i][j] = max(dp[k-1][i][j],dp[k-1][i-num_0][j-num_1]+1)(3)初始化:
由于压缩的是物品那一维度,所以初始化时,设物品为空,此时子集的数量永远为0

(4)遍历顺序:
常规
完整代码如下:
class Solution {
public:
int count(string str){
int sum = 0;
for(int i = 0; i < str.size();i++)
sum +=str[i] - '0';
return sum;
}
int findMaxForm(vector<string>& strs, int m, int n) {
int size = strs.size();
vector<vector<int>> dp(m+1,vector<int>(n+1,0));
for(int k = 0;k < size;k++){
int x = count(strs[k]);//1
int y = strs[k].size() - x; //0
for(int i = m;i >= y;i--)
for(int j = n;j >= x;j--){
dp[i][j] =max(dp[i][j],dp[i-y][j-x]+1);
}
}
return dp[m][n];
}
};2.完全背包
2.1 完全背包框架
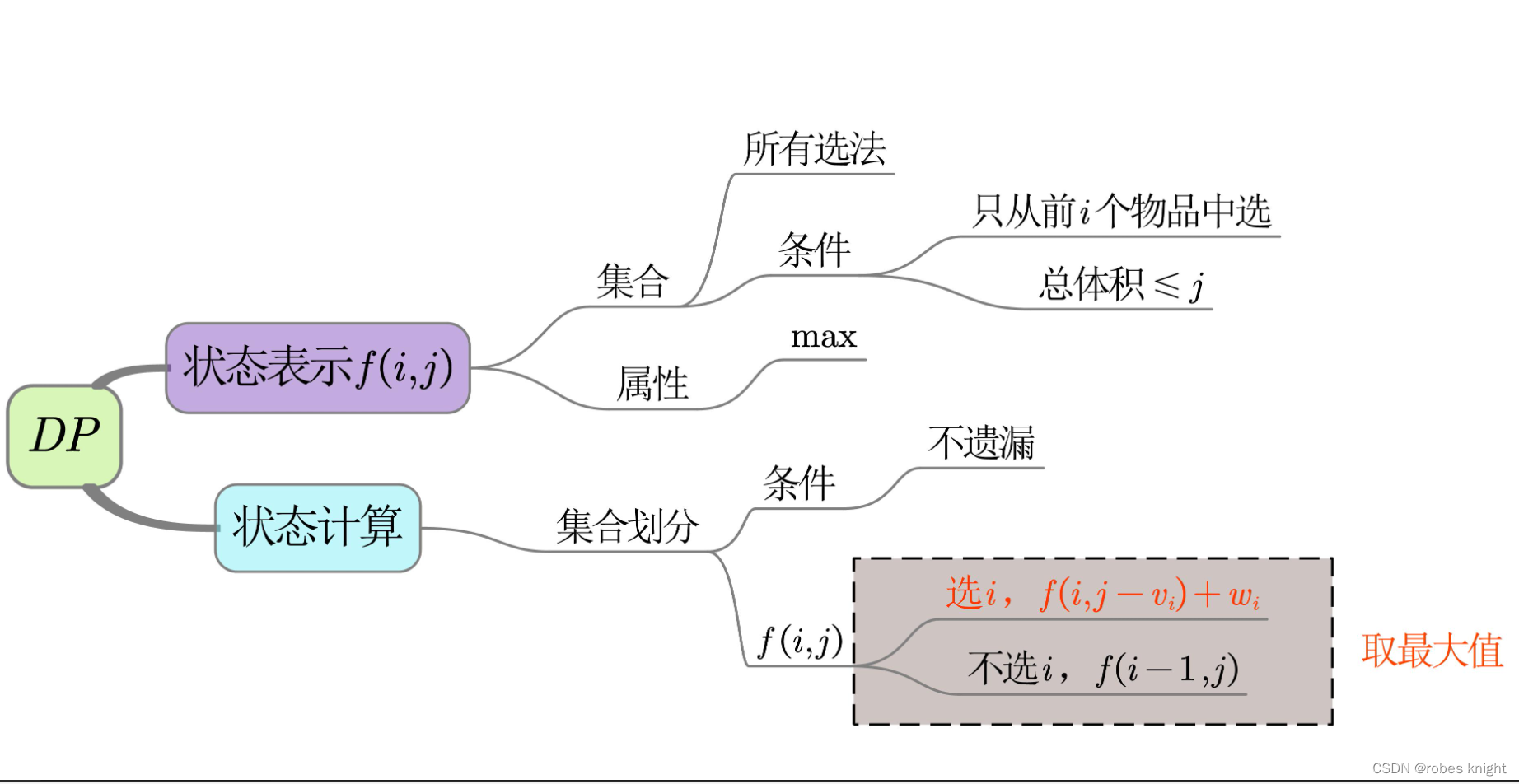
(1)dp定义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
(2)转移方程
未优化:
// 未优化
int f[N][M]; // f[i][j]表示在考虑前i个物品后,背包容量为j条件下的最大价值
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
for (int k = 0; k * v[i] <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);根据下式进行优化:

优化后:
// 已优化
int f[N][M]; // f[i][j]表示在考虑前i个物品后,背包容量为j条件下的最大价值
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
if(j < v[i]) f[i][j] = f[i-1][j]; // 当前重量装不进,价值等于前i-1个物品
else f[i][j] = max(f[i-1][j], f[i][j-v[i]] + w[i]); // 能装,需判断 因此最终形式和01背包类似:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);(3)初始化
按照之前的写法就行
(4)遍历顺序--重点
我们注意,完全背包的转移方程如下:
dp[i][j] = max(dp[i-1][j], dp[i][j-weight[i]] + value[i]);对比01背包的转移方程:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); dp[i][j]并不是只和上一行有关系,dp[i][j]是由上一行的dp[i-1][j]和这一行的dp[i][j-weight[i]] + value[i]求得,因此我们改变遍历顺序,使得每次先将dp[i-1][j-weight]更新为dp[i][j-weight[i]]再与dp[i-1][j]进行求解
使用从左向右遍历的顺序就能达到这种效果
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}重点来了:
这里纯完全背包两个for循环的先后循序,都不影响计算dp[j]所需要的值,但是!!!,对于排列和组合问题就不一样了
(1)先物品后背包(结果只含一种顺序)
这是常用的容易理解的顺序,为什么说这个顺序是容易理解呢,我们看这样的图:
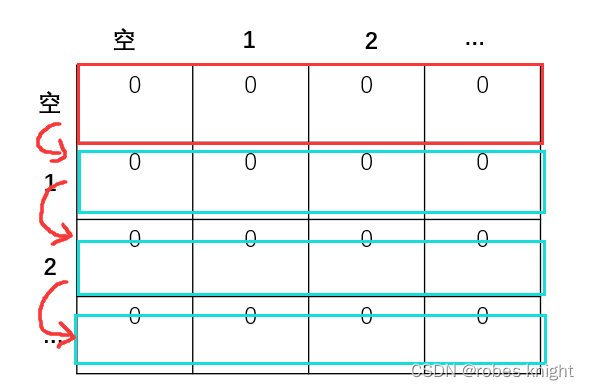
因为使用的一维数组,压缩了行(注意压缩的是行不是列),而且更据dp数组的定义,我们初始化的是第一行,而先物品后背包的顺序正是这样从上往下滚动更新(按照物品顺序)
(2)先物品后背包(结果包含不同顺序的组合)
其更新如下图:
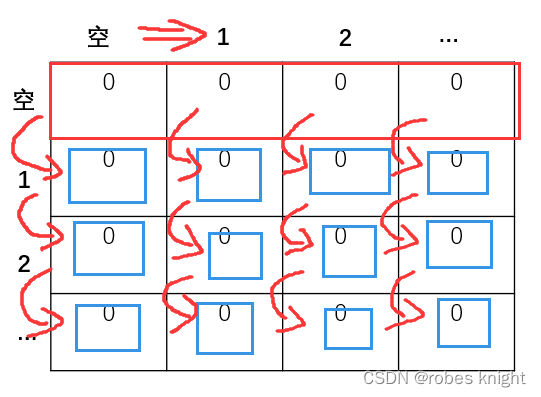
由于dp定义相同,因此初始化也是对第一行进行初始化,但是由于先背包后物品,我们在更新的时候会先更新第一列,再第二列,这样类推
也就是第i列更新后只改变了dp[i],此时dp[i+1]还是初始化的状态,如下图(图中的数值乱写的,主要看红框(dp[j]的变化)):



这样遍历的特点是:
可以使用左下角的元素来更改当前值,也即是可以使得结果中包含不同顺序的组合
举例说明:
如果先遍历背包后遍历物品,那么外层循环先固定背包大小j,然后在大小为j的背包中循环遍历添加物品,然后在下次外层循环背包大小变为j+1,此时仍要执行内层循环遍历添加物品,也就会出现在上一轮外层循环中添加coins【2】的基础上还能再添加coins【1】的情况,那么就有了coins【1】在coins【2】之后的情况了。
2.2 完全背包例题
2.2.1 组合总和4(究极重要的理解遍历顺序的题)

这道和前面的求组合的题比较像,但是有一点很重要,此题要求不同顺序算不同组合,也即是我们
不能使用单一的顺序进行遍历
此题重点在于遍历顺序,递归方程和前面的求路径的问题一样
1.二维解法
此题的二维解法非常难想,就是因为这题要求考虑不同顺序
(1)dp[i][j]定义为i个数组合为j的组合数
(2)转移方程:同样压缩行
dp[i][j] =dp[i][j] + dp[i][j-nums[k-1]];(3)根据dp定义,第一列为1,其余0
(4)遍历顺序
这里无论哪种顺序都是一样,因为上面我们说的是一维数组,更新的时候,只保留了最后一行的值(dp[j]前面的值其实包含了左边所有信息),但是二维数组更新了所有地方的值,dp[i][j]就只能根据左上方进行更新了
也就是说,我们按照for循环从前往后,前面使用过的元素,后面用不了了,也就是考虑不到多种顺序的影响
所以,我们应该加一层循环,将当前值之前的所有值都重新拿来判断,代码如下:
//前两行顺序可换
for(int i = 1;i <= n;i++)
for(int j = 1;j <=target;j++)
for(int k = 1;k <= i;k++){
if (j >= nums[k-1]) {
dp[i][j] =dp[i][j] + dp[i][j-nums[k-1]];
}
}完整代码如下:
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
int n = nums.size();
vector<vector<unsigned int>> dp(n+1,vector<unsigned int>(target+1,0));
for(int i = 0;i <= n;i++)dp[i][0] = 1;
//前两行顺序可换
for(int i = 1;i <= n;i++)
for(int j = 1;j <=target;j++)
for(int k = 1;k <= i;k++){
if (j >= nums[k-1]) {
dp[i][j] =dp[i][j] + dp[i][j-nums[k-1]];
}
}
return dp[n][target];
}
};2.一维解法
(1)dp定义,凑成目标正整数为i的排列个数为dp[i]
(2)转移方程,相同
dp[j] += dp[j - nums[i]];(3)初始化,根据定义写就行了

(4)遍历顺序
由于是一维数组,就·可以用到之前说的先背包后物品的顺序,使得前面考虑过的物品,后面还能重新考虑,思路见 2.1(4)
代码如下:
for (int j = 0 ; j <= target; j++) {
for (int i = 0; i < n; i++) {
if (j >= nums[i])
{
dp[j] += dp[j - nums[i]];
}
}
}完整代码:
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
int n = nums.size();
vector<unsigned int> dp(target + 1);
dp[0] = 1;
for (int j = 0 ; j <= target; j++) {
for (int i = 0; i < n; i++) {
if (j >= nums[i])
{
dp[j] += dp[j - nums[i]];
}
}
}
return dp[target];
}
};
2.2.2 单词拆分--转移方程太难写了

本题一眼能看出是背包问题,我们将worddict中的单词填入字符背包s中,能正好装满返回true,否则false
但是细想却很难和前面的背包融会贯通,因为之前的背包,我们可以随意放入,改变背包容量j时,减去重量即可,
但是,这里的背包一个单词只能放在一个固定的位置上,如果我们随意放,将单词放在了背包中间位置,我们就不能通过减去单词的size来获取前一个背包用来更新当前背包
所有本题的核心有点类似子序列,由于更新dp数组的方法比较固定(减去当前放入的单词的大小),那么我们每次就只判断最后一段能不能放入单词,如果能放入,就使用dp[j - word.size()]更新,如果不能就保持原样(false),接着找其他单词进行匹配
(1)dp定义:
dp[j]为s的【0,j】部分作为背包,将worddict放入,能放满就是1,否则0
(2)转移方程:
这是这一题的关键,我们能想到的更新dp数组的方法有限,要么从dp[j]要么从dp[j - size]更新,所以我们只对最后一段字符进行处理
代码如下:
if(j>=wordDict[i].size()){
string str = s.substr(j-wordDict[i].size(),wordDict[i].size());
if(str == wordDict[i] &&dp[j-wordDict[i].size()])
dp[j] = dp[j-wordDict[i].size()] ;
}每次判断最后一段字符,有两种情况:
1)和word[i]相同:
那么这一段可以抵消, dp[j] = dp[j-wordDict[i].size()]
那么为什么要加上&&dp[j-wordDict[i].size()]呢,下如图:
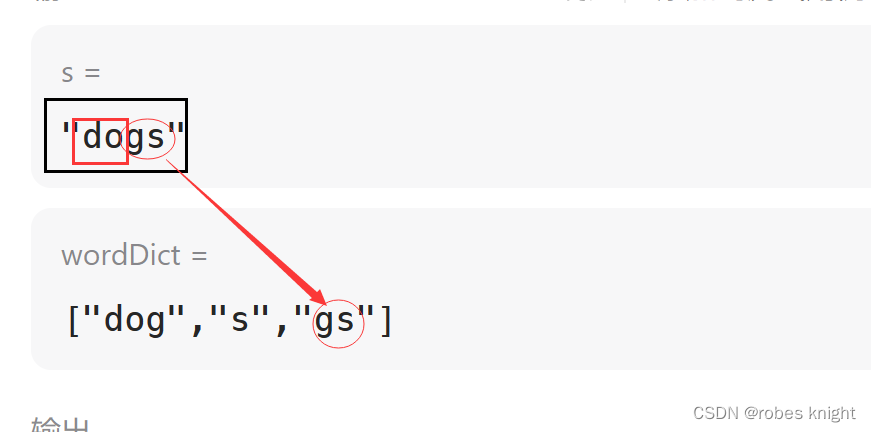
dp[j-wordDict[i].size()](红框)为假,且最后一段字符能够匹配,但是dp[j]却是真
因为我们没有判断dp[j-wordDict[i].size()]是否为真,实际上只有dp[j-wordDict[i].size()]为真时,dp[j] = dp[j-wordDict[i].size()]才成立
当dp[j-wordDict[i].size()]为假时,我们无法判断,如何得到真
但是如果一个背包可以被装满,那么在去除最后一段字符后,剩下的dp[j-wordDict[i].size()]一定为真,从真推到真是一定可以走通的,也就是说我们没必要走从dp[j-wordDict[i].size()]为假再推导到dp[j]为真的路径,那么就不用管当dp[j-wordDict[i].size()]为假时的情况
2)和word[i]不同:
保持原样,继续遍历其他word,找到就跳到1),找不到,就还是0(初始值)
(3)初始化:

(4)遍历顺序:
由于一个单词可能会多次放入,因此使用先背包后物品
完整代码如下:
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordset(wordDict.begin(),wordDict.end());
int n = s.size();
vector<int> dp(n+1,0);
dp[0] = 1;
for(int j = 0;j <=n;j++)
for(int i = 0;i < wordDict.size(); i++)
if(j>=wordDict[i].size()){
string str = s.substr(j-wordDict[i].size(),wordDict[i].size());
if(str == wordDict[i])
dp[j] = dp[j-wordDict[i].size()] ||dp[j];
}
return dp[n];
}
};2.2.3 零钱兑换2
由于是求最优组合,且每种硬币可以重复使用,所有使用先物品后背包的完全背包
只要明确了方法和遍历顺序,其他细节都和前面的题差不多,完整代码如下:
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<int> dp(amount+1,0);
dp[0] = 1;
int n = coins.size();
for(int i = 0; i <n; i++)
for(int j = coins[i];j<=amount;j++){
dp[j] = dp[j] + dp[j-coins[i]];
}
return dp[amount];
}
};2.2.4 完全平方数

这道题首先要明确如何转换为背包, 我们看到n的限制为10000,所以最多使用到100^2
也就相当于将0-100的i,我们将i^2当作物品放入总数为n的背包,求最优组合
(1)dp定义:
dp[j]为容量为j的背包,放满能放入的最小数量
(2)转移方程:
判断每一个物品i*i是否放入
dp[j] =min(dp[j],dp[j - i*i]+1);(3)初始化:
dp[0]需要注意,其余位置,由于是求最小数量,那么我们要给一个较大值防止更新能够成功
(4)遍历顺序:
先物品后背包
完整代码如下:
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n+1,10000);
dp[0] = 0;
for(int i = 1; i <=100;i++ )
for(int j = 0;j <= n;j++)
if(j >= i*i)
dp[j] =min(dp[j],dp[j - i*i]+1);
return dp[n];
}
};






















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








