CINTA第5次作业
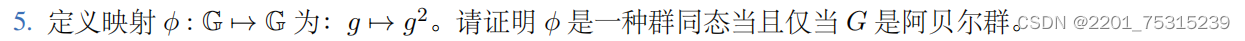
证明: 充分性: ∵ ϕ 是一种群同态 ∴ ∀ a , b ∈ G , ϕ ( a ⋅ b ) = ϕ ( a ) ◦ ϕ ( b ) ∴ ( a b ) 2 = a 2 b 2 ∴ a b = a 2 b 2 ( a b ) − 1 = a 2 b a − 1 ∴ b = a b a − 1 , 即 b a = a b ∴ G 是阿贝尔群 必要性: ∵ G 是阿贝尔群 ∴ ∀ a , b ∈ G , 有 b a = a b ∴ a b b a = a b a b , 即 a a b b = a b a b ∴ a 2 b 2 = ( a b ) 2 , 满足 ϕ ( a ⋅ b ) = ϕ ( a ) ◦ ϕ ( b ) ∴ ϕ 是一种群同态 \begin{aligned} 充分性:&\because \phi是一种群同态\\ &\therefore\forall a,b\in \mathbb{G},\phi(a·b)=\phi(a)◦\phi(b)\\ &\therefore (ab)^2=a^2b^2\\ &\therefore ab=a^2b^2(ab)^{-1}=a^2ba^{-1}\\ &\therefore b=aba^{-1},即ba=ab\\ &\therefore \mathbb{G}是阿贝尔群\\ 必要性:&\because \mathbb{G}是阿贝尔群\\ &\therefore \forall a,b\in \mathbb{G},有ba=ab\\ &\therefore abba=abab,即aabb=abab\\ &\therefore a^2b^2=(ab)^2,满足\phi(a·b)=\phi(a)◦\phi(b)\\ &\therefore \phi是一种群同态 \end{aligned} 充分性:必要性:∵ϕ是一种群同态∴∀a,b∈G,ϕ(a⋅b)=ϕ(a)◦ϕ(b)∴(ab)2=a2b2∴ab=a2b2(ab)−1=a2ba−1∴b=aba−1,即ba=ab∴G是阿贝尔群∵G是阿贝尔群∴∀a,b∈G,有ba=ab∴abba=abab,即aabb=abab∴a2b2=(ab)2,满足ϕ(a⋅b)=ϕ(a)◦ϕ(b)∴ϕ是一种群同态

证明:
∵
G
是循环群
,
且
∀
a
,
b
∈
G
有
ϕ
(
a
b
)
=
ϕ
(
a
)
ϕ
(
b
)
∴
∀
g
∈
G
且存在整数
k
使
g
=
g
k
,
有
ϕ
(
g
)
=
ϕ
(
g
k
)
=
ϕ
(
g
)
ϕ
(
g
)
…
ϕ
(
g
)
=
ϕ
(
g
)
k
∴
ϕ
(
G
)
也是循环群
∵
G
是交换群
,
且
∀
a
,
b
∈
G
有
ϕ
(
a
b
)
=
ϕ
(
a
)
ϕ
(
b
)
∴
∀
a
,
b
∈
G
,
有
a
b
=
b
a
∴
ϕ
(
a
)
ϕ
(
b
)
=
ϕ
(
a
b
)
=
ϕ
(
b
a
)
=
ϕ
(
b
)
ϕ
(
a
)
∴
ϕ
(
G
)
也是交换群
\begin{aligned} &\because \mathbb{G}是循环群,且\forall a,b\in \mathbb{G}有\phi (ab)=\phi(a)\phi(b)\\ &\therefore \forall g\in \mathbb{G}且存在整数k使g=g^k,有\phi(g)=\phi(g^k)=\phi(g)\phi(g)…\phi(g)=\phi(g)^k\\ &\therefore \phi( \mathbb{G})也是循环群\\ &\\ &\because \mathbb{G}是交换群,且\forall a,b\in \mathbb{G}有\phi (ab)=\phi(a)\phi(b)\\ &\therefore \forall a,b\in \mathbb{G},有ab=ba\\ &\therefore \phi(a)\phi(b)=\phi (ab)=\phi(ba)=\phi(b)\phi(a)\\ &\therefore \phi( \mathbb{G})也是交换群\\ \end{aligned}
∵G是循环群,且∀a,b∈G有ϕ(ab)=ϕ(a)ϕ(b)∴∀g∈G且存在整数k使g=gk,有ϕ(g)=ϕ(gk)=ϕ(g)ϕ(g)…ϕ(g)=ϕ(g)k∴ϕ(G)也是循环群∵G是交换群,且∀a,b∈G有ϕ(ab)=ϕ(a)ϕ(b)∴∀a,b∈G,有ab=ba∴ϕ(a)ϕ(b)=ϕ(ab)=ϕ(ba)=ϕ(b)ϕ(a)∴ϕ(G)也是交换群
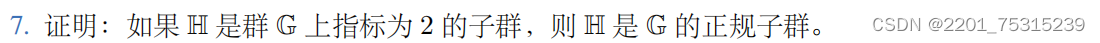
证明:
∵
[
G
:
H
]
=
2
∴
H
在
G
上不相同的左陪集的个数为
2
设
H
的左陪集分别为
H
1
、
H
2
∀
g
∈
G
,当
g
落在
H
1
时,则
g
H
1
=
H
1
=
H
1
g
当
g
落在
H
2
时,则
g
H
2
=
H
2
=
H
2
g
∴
∀
g
∈
G
,
g
H
=
H
g
∴
H
是
G
的正规子群
\begin{aligned} &\because [\mathbb{G}:\mathbb{H}]=2\\ &\therefore \mathbb{H} 在 \mathbb{G} 上不相同的左陪集的个数为2\\ &设\mathbb{H}的左陪集分别为\mathbb{H}_1、\mathbb{H}_2\\ &\forall g\in\mathbb{G},当g落在\mathbb{H}_1时,则g\mathbb{H}_1=\mathbb{H}_1=\mathbb{H}_1g\\ &当g落在\mathbb{H}_2时,则g\mathbb{H}_2=\mathbb{H}_2=\mathbb{H}_2g\\ &\therefore \forall g\in \mathbb{G},g\mathbb{H}=\mathbb{H}g\\ &\therefore \mathbb{H}是\mathbb{G}的正规子群\\ \end{aligned}
∵[G:H]=2∴H在G上不相同的左陪集的个数为2设H的左陪集分别为H1、H2∀g∈G,当g落在H1时,则gH1=H1=H1g当g落在H2时,则gH2=H2=H2g∴∀g∈G,gH=Hg∴H是G的正规子群

证明:
∵
H
是群
G
的正规子群
,
商群
G
/
H
=
{
g
H
,
g
∈
G
}
∴
∀
g
1
H
,
g
2
H
∈
G
/
H
,
有
(
g
1
H
)
(
g
2
H
)
=
g
1
g
2
H
∵
群
G
是阿贝尔群
∴
∀
a
,
b
∈
G
,
有
a
b
=
b
a
∴
∀
g
1
,
g
2
∈
G
,
(
g
1
H
)
(
g
2
H
)
=
g
1
g
2
H
=
g
2
g
1
H
=
(
g
2
H
)
(
g
1
H
)
∴
商群
G
/
H
也是阿贝尔群
\begin{aligned} &\because \mathbb{H}是群\mathbb{G}的正规子群,商群\mathbb{G}/\mathbb{H}=\{g\mathbb{H},g\in \mathbb{G}\}\\ &\therefore \forall g_1\mathbb{H},g_2\mathbb{H}\in \mathbb{G}/\mathbb{H},有(g_1\mathbb{H})(g_2\mathbb{H})=g_1g_2\mathbb{H}\\ &\because 群\mathbb{G}是阿贝尔群\\ &\therefore \forall a,b\in\mathbb{G},有ab=ba\\ &\therefore \forall g_1,g_2\in\mathbb{G},(g_1\mathbb{H})(g_2\mathbb{H})=g_1g_2\mathbb{H}=g_2g_1\mathbb{H}=(g_2\mathbb{H})(g_1\mathbb{H})\\ &\therefore 商群\mathbb{G}/\mathbb{H}也是阿贝尔群\\ \end{aligned}
∵H是群G的正规子群,商群G/H={gH,g∈G}∴∀g1H,g2H∈G/H,有(g1H)(g2H)=g1g2H∵群G是阿贝尔群∴∀a,b∈G,有ab=ba∴∀g1,g2∈G,(g1H)(g2H)=g1g2H=g2g1H=(g2H)(g1H)∴商群G/H也是阿贝尔群

证明:
∵
H
是群
G
的正规子群
,
商群
G
/
H
=
{
g
H
,
g
∈
G
}
∴
∀
g
1
H
,
g
2
H
∈
G
/
H
,
有
(
g
1
H
)
(
g
2
H
)
=
g
1
g
2
H
∵
群
G
是循环群
∴
∀
g
∈
G
,
存在整数
k
使
g
=
g
k
∴
g
H
=
g
k
H
=
(
g
H
)
(
g
H
)
…
(
g
H
)
=
(
g
H
)
k
∴
商群
G
/
H
也是循环群
\begin{aligned} &\because \mathbb{H}是群\mathbb{G}的正规子群,商群\mathbb{G}/\mathbb{H}=\{g\mathbb{H},g\in \mathbb{G}\}\\ &\therefore \forall g_1\mathbb{H},g_2\mathbb{H}\in \mathbb{G}/\mathbb{H},有(g_1\mathbb{H})(g_2\mathbb{H})=g_1g_2\mathbb{H}\\ &\because 群\mathbb{G}是循环群\\ &\therefore \forall g\in\mathbb{G},存在整数k使g=g^k\\ &\therefore g\mathbb{H}=g^k\mathbb{H}=(g\mathbb{H})(g\mathbb{H})…(g\mathbb{H})=(g\mathbb{H})^k\\ &\therefore 商群\mathbb{G}/\mathbb{H}也是循环群\\ \end{aligned}
∵H是群G的正规子群,商群G/H={gH,g∈G}∴∀g1H,g2H∈G/H,有(g1H)(g2H)=g1g2H∵群G是循环群∴∀g∈G,存在整数k使g=gk∴gH=gkH=(gH)(gH)…(gH)=(gH)k∴商群G/H也是循环群





















 626
626











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








