【优化调度】基于遗传算法的公交车调度排班优化的研究与实现（Matlab代码实现）-CSDN博客

本文链接：https://blog.csdn.net/2201_75535220/article/details/147635460

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

基于遗传算法的公交车调度排班优化研究

一、遗传算法的基本原理及在调度问题中的应用

二、公交车调度排班问题的建模与约束条件

三、适应度函数设计的关键要素

四、遗传算法参数设置对调度效果的影响

五、数据集获取与测试案例

六、遗传算法与传统方法的性能对比

七、研究展望与挑战

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据

💥1 概述

基于遗传算法的公交车调度排班优化研究

一、遗传算法的基本原理及在调度问题中的应用

遗传算法核心机制
遗传算法（GA）通过模拟生物进化过程（选择、交叉、变异）解决优化问题，其核心步骤包括：
- 编码：将调度方案转化为染色体（如整数编码表示班次发车时间或车辆路径）。
- 适应度函数：评估调度方案的优劣，如结合乘客等待时间、运营成本等指标。
- 选择操作：基于适应度值筛选优质个体（如轮盘赌选择或锦标赛选择）。
- 交叉与变异：通过基因重组（如顺序交叉OX）和随机扰动（如插入变异）增强种群多样性。
在调度问题中的优势
- 全局搜索能力：适合处理多约束、非线性的复杂问题（如发车间隔、车辆容量限制）。
- 多目标优化：可平衡乘客满意度（等待时间）与运营成本（车辆数、行驶距离）。
- 并行计算：适用于大规模公交网络的高效求解。

二、公交车调度排班问题的建模与约束条件

优化目标
- 乘客端：最小化平均等待时间、提高满载率均衡性。
- 运营端：最小化总行驶距离、车辆使用数及能源消耗（如电动公交电量约束）。
关键约束条件
- 时间窗约束：

发车间隔限制（如早高峰最小间隔2分钟，非高峰最大间隔15分钟）。
订单服务时间窗口（确保乘客上下车时间在预期范围内）。
数学表达：
ET_i \leq t_{i,k} \leq LT_i \quad \text{（任务i的开始时间在[ET_i, LT_i]内）}
- 车辆容量限制：
最大载客量（如公交车座位数限制）。
数学表达：
∑i=1Nqixi≤C（车辆k在任务i时的载客量不超过C）∑i=1Nqixi≤C（车辆k在任务i时的载客量不超过C）
- 其他约束：车辆路径连续性、充电桩使用限制（电动公交）。

三、适应度函数设计的关键要素

设计原则
- 问题导向性：需反映调度目标，如将乘客等待时间与运营成本加权组合。
- 区分度与效率：快速计算且能明确区分优劣方案（如非线性函数优于线性函数）。
- 避免局部最优：通过惩罚项处理违反约束的方案（如超载或超时）。
示例函数

Fitness=α⋅乘客等待时间+β⋅运营成本+γ⋅约束违反惩罚Fitness=α⋅乘客等待时间+β⋅运营成本+γ⋅约束违反惩罚

其中，α,β,γα,β,γ为权重系数，需根据实际需求调整。

四、遗传算法参数设置对调度效果的影响

参数优化策略
- 种群规模：通常取50-100，规模过小易早熟，过大则计算成本高。
- 交叉率（0.4-0.9） ：高交叉率增强搜索广度，但可能破坏优良基因。
- 变异率（0.01-0.1） ：低变异率保持稳定性，高变异率增强多样性。
- 终止条件：迭代次数（如500代）或适应度值稳定阈值。
实验验证
- 案例显示，参数设置为种群50、交叉率0.7、变异率0.1时，算法收敛速度与解质量较优。

五、数据集获取与测试案例

数据来源
- 公交IC卡与GPS数据：获取乘客上下车时间、站点客流分布。
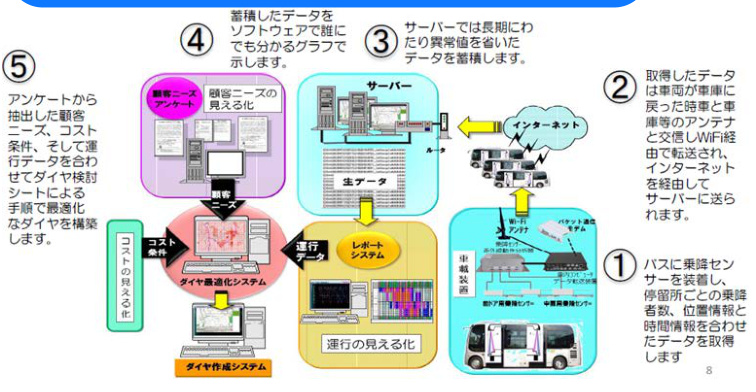
- 传感器数据：实时监控车辆位置、载客量及电池状态（电动公交）。
典型测试案例
- 哈尔滨市公交线路：通过调整发车间隔与首班车时间，乘客出行时间减少15%。
- 南京公交IC卡分析：结合历史数据优化高峰时段发车频率，满载率均衡性提升20%。

六、遗传算法与传统方法的性能对比

对比指标
- 收敛速度：GA在复杂问题中收敛更快（如改进GA比传统GA快30%）。
- 解的质量：GA在多目标优化中更优（如碳排放减少38吨，成本降低2.95万元）。
- 可扩展性：GA适合动态调整（如实时客流变化），而线性规划难以处理非线性约束。
案例结果
- 水土保持项目调度中，GA比传统表上作业法节省运费13.75万元。

七、研究展望与挑战

改进方向
- 混合算法：结合粒子群优化（PSO）或禁忌搜索提升局部搜索能力。
- 动态适应度函数：根据实时客流调整权重系数（如高峰时段侧重乘客体验）。
实际应用难点
- 数据实时性：需与GPS、客流预测系统集成以实现动态调度。
- 计算效率：大规模路网需设计并行计算框架（如分布式GA）。

📚2 运行结果

主函数代码：

clear;clc;close all
%% 载入模型参数
LoadData();

%% 参数设置
PopSize = 50;
MaxGen = 100;
plt = 1; % 运行过程是否实时画迭代优化图，默认关闭(可极大提高运行速度)

%% 初始化
Population = Init(PopSize);
ConvergenceObj = zeros(2,PopSize);
ConvergenceCon = zeros(2,PopSize);

% return
%% 开始优化求解
h = figure();
for gen = 1:MaxGen
MatingPool = randperm(PopSize,PopSize); %父代挑选
Offspring = GA(Population(MatingPool)); %进行交叉变异操作
Population = EnviornmentalSelection(Population,Offspring,gen/MaxGen); %挑选子代
RecordInfo(); % 记录迭代优化信息
end
BestSol = BestInd(end);
disp(['发车时间间隔：' num2str(BestSol.decs)])
disp(['时段发车数量：' num2str(floor(60./BestSol.decs))])
disp(['乘客总时间成本:' num2str(BestSol.Q) ', 公交公司运行费用:' num2str(BestSol.G)])
disp(['总体载客率：' num2str(100*BestSol.zaikelv) '%'])
figure
yyaxis right
plot(BestSol.decs,'-s','linewidth',2)
ylabel('发车时间间隔/分钟')
hold on
yyaxis left
plot(bus.C,'-d','linewidth',2)
ylabel('客流量')
xlabel('时段')