R语言统计学-参数估计（求置信区间）、假设检验（总体比例检验、计算效应量）

1、参数估计（两个总体均值差求置信区间）

（统计学-基于R-第五版-第六章习题6.3）

        顾客到银行办理业务时往往需要等待一些时间，等待时间的长短与许多因素有关，比如，银行的业务员办理业务的速度、顾客等待排队的方式等。为此，某银行准备采取两种排队方式进行试验，第一种排队方式是所有顾客都进入一个等待队伍；第二种排队方式是顾客在三个业务窗口处排队等待。为比较哪种排队方式使顾客等待的时间更短，银行各随机抽取10名顾客，他们在办理业务时等待的时间（单位：分钟）如下：

（1）构建第一种排队方式等待时间均值的95%的置信区间。

（2）构建第二种排队方式等待时间方差的95%的置信区间。

（3）构建两种方式排队时间均值差值的95%的置信区间：①假设σ₁²=σ₂²；②假设σ₁²≠σ₂²

        实现代码和结果：

example4<-read.csv("C:/Users/lenovo/OneDrive/大二/大数据统计学实验/实验表格/银行业务办理等待时间表格.csv")
#计算第一种排队方式等待时间均值的95%的置信区间
t.test(example4$方式1)$conf.int
#计算第二种排队方式等待时间方差的95%的置信区间
t.test(example4$方式2)$conf.int

#计算两种方式排队时间均值差值的95%的置信区间
x=example4$方式1;y=example4$方式2
#假设方差σ₁²=σ₂²
t.test(x,y,var.equal = TRUE)$conf.int
#假设方差σ₁²≠σ₂²
t.test(x,y,var.equal = FALSE)$conf.int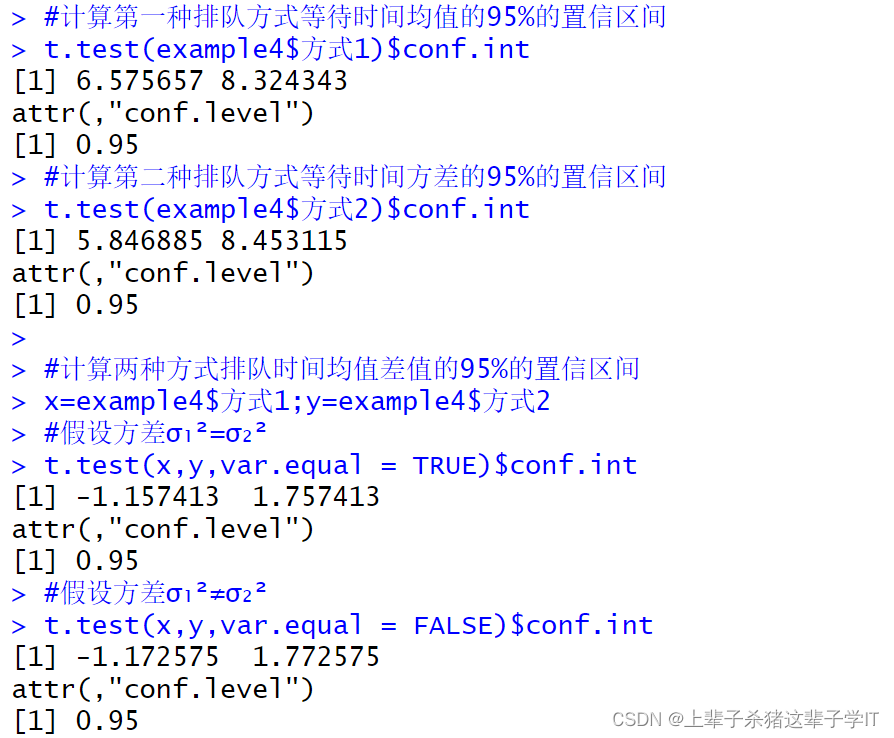

        计算结果表示排队方式1等待时间均值95%的置信区间为6.575657~8.324343分钟。排队方式2等待时间均值95%的置信区间为5.846885~8.453115分钟。

        比较两种排队方式的置信水平，直接将各自数据导入t.test函数中，var.equal=TRUE表示方差相等时的情况，var.equal=FALSE表示方差不相等的情况。假设σ₁²=σ₂²时，两种排队方式等待时间均值差值的95%的置信区间为-1.157413~1.757413分钟；假设σ₁²≠σ₂²时，两种排队方式等待时间均值差值的95%的置信区间为-1.172575~1.772575分钟。

2、假设检验（两个总体均值差和总体比例的检验）

（统计学-基于R-第五版-第七章习题7.4）

        某企业为比较两种方法对员工培训的效果，采用方法1对15名员工进行培训，采用方法2对另外15名员工进行培训。培训后的测试分数如下：

在α=0.05的显著性水平下，检验两种方法的培训效果是否有显著差异。

（1）假定方差相等。

（2）假定方差不相等。

（3）计算效应量，分析差异程度。

        实现代码和结果：

example5<-read.csv("C:/Users/lenovo/OneDrive/大二/大数据统计学实验/实验表格/员工培训测试数据.csv")
#假设总体方差相等
t.test(example5$方法1,example5$方法2,var.equal=TRUE)
#假设总体方差不相等
t.test(example5$方法1,example5$方法2,var.equal=FALSE)
#计算效应量
library(lsr)
cohensD(example5$方法1,example5$方法2)

        方法1的平均数为47.73333，方法2的平均数为56.73333。假设总体方差相等时，t = -5.8927, df = 28, p-value = 2.444e-06；假设总体方差不相等时，t = -5.8927, df = 27.639, p-value = 2.568e-06。

        效应量d=2.151704，表明方法1和方法2的平均测试分数的样本均值差值与总体均值差值相差2.151704个标准差，根据Cohen准则（独立样本t检验的小、中、大效应量对应的d值分别为0.20、0.50、0.80），该检验结果属于大的效应量。

（统计学-基于R-第五版-第七章习题7.5）

        对消费者的一项调查显示，17%的人早餐饮料是牛奶。某城市的牛奶生产商认为，该城市的人早餐饮用牛奶的比例更高。为验证这一说法，生产商随机抽取550人的一个随机样本，其中115人早餐饮用牛奶。检验该生产商的说法是否属实（α=0.05）。

        实现代码和结果：

n<-550     #随机样本数
p<-115/550
pi0<-0.17
z<-(p-pi0)/sqrt(pi0*(1-pi0)/n)
p_value<-1-pnorm(z)
data.frame(z,p_value)

        调查显示17%的人早餐饮料是牛奶，因此提出假设为

        H₀：Π⩽17%；H₁：Π>17%

        在该检验中，z=2.440583，P=0.007331785，由于P<0.05，拒绝H₀，可以证明该生产商的说法属实。