大学物理绪论组收集和分析

目录

​编辑

随机误差的估计

算术平均值的标准偏差

 不确定度（Uncertainty）是测量学中的一个重要概念，用于表示测量结果的可靠程度。它反映了测量值可能偏离真值（即被测量的客观真实值）的程度。

A类不确定度的计算方法

 

以下是一个Python代码示例，用于计算A类不确定度（标准偏差）：

 B类不确定度

 间接测量结果不确定度的合成

假设我们有一个间接测量量 \( Y = f(X_1, X_2, \ldots, X_n) \)，其中 \( X_i \) 是直接测量量，\( f() \) 是包含这些直接测量量的函数。我们已经知道了每个直接测量量 \( X_i \) 的不确定度 \( \Delta X_i \)。

以下是一个Python函数示例，它接受一个函数f（表示间接测量量与直接测量量之间的关系）、一个包含直接测量量值的列表x_values以及一个包含直接测量量不确定度的列表delta_x_values，然后返回间接测量结果的不确定度delta_y：

 对数微分法

 Python代码来演示对数微分法：

---

随机误差的估计

不可控制的因素影响而产生的误差。这些因素可能是测量环境的微小变化、测量设备的不稳定、甚至是操作人员的微小动作变化等。随机误差使得在同一条件下对同一量进行多次测量时，得到的结果会时大时小、时正时负，呈现出随机性。

随机误差的估计通常涉及以下几个方面：

1. 多次测量：通过多次测量并计算平均值，可以减小随机误差的影响。这是因为随机误差在多次测量中会有所抵消。多次测量的平均值比单次测量值更接近真实值。

2. 标准偏差：标准偏差（σ）是衡量随机误差大小的一个重要参数。它反映了测量数据的离散程度。在统计学中，标准偏差可以通过测量数据的平方差的平均值的平方根来计算。

3. 贝塞尔公式：贝塞尔公式用于估计随机误差的大小，它表明在一定置信水平下（例如68.3%），随机误差的绝对值不会超过某个数值。这为随机误差的控制提供了依据。

4. 置信区间：置信区间是根据一定置信水平（例如95%），由统计方法推断出的测量结果可能的区间范围。这意味着该区间包含真实值的概率为指定的置信水平。

5. 相对误差：相对误差是随机误差绝对值与测量结果之比，通常用来衡量随机误差对测量结果的影响程度。

算术平均值的标准偏差

算术平均值的标准偏差（或称为标准误差）通常用于估计样本均值与总体均值之间的差异。当我们只有样本数据时，我们不知道总体的真实均值，但我们可以使用样本均值作为估计，并使用标准偏差来量化这个估计的不确定性。

样本的标准偏差（SD）和样本大小（n）之间的关系用于计算算术平均值的标准偏差（也称为标准误差，SE）。标准误差的计算公式为：

SE = SD / √n

其中，SD 是样本的标准偏差，n 是样本大小（即样本中的观测值数量）。

以下是一个使用 Python 计算算术平均值的标准偏差的示例：

import numpy as np  
  
# 假设我们有一个样本数据  
sample_data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])  
  
# 计算样本的算术平均值  
sample_mean = np.mean(sample_data)  
  
# 计算样本的标准偏差  
sample_sd = np.std(sample_data, ddof=1)  # ddof=1 是为了得到样本的标准偏差的无偏估计  
  
# 计算算术平均值的标准偏差（标准误差）  
n = len(sample_data)  
se = sample_sd / np.sqrt(n)  
  
print(f"样本的算术平均值: {sample_mean}")  
print(f"样本的标准偏差: {sample_sd}")  
print(f"算术平均值的标准偏差（标准误差）: {se}")

 不确定度（Uncertainty）是测量学中的一个重要概念，用于表示测量结果的可靠程度。它反映了测量值可能偏离真值（即被测量的客观真实值）的程度。

1. A类不确定度（也称为统计不确定度）：来源于随机因素，如测量过程中的偶然误差，其大小可通过统计方法获得，例如通过观测测量结果的分布来估算。

2. B类不确定度（也称为系统不确定度）：来源于可确定的非随机因素，如仪器的校准误差、环境条件的变化等，其大小可通过分析和评估各种影响因素来估算。

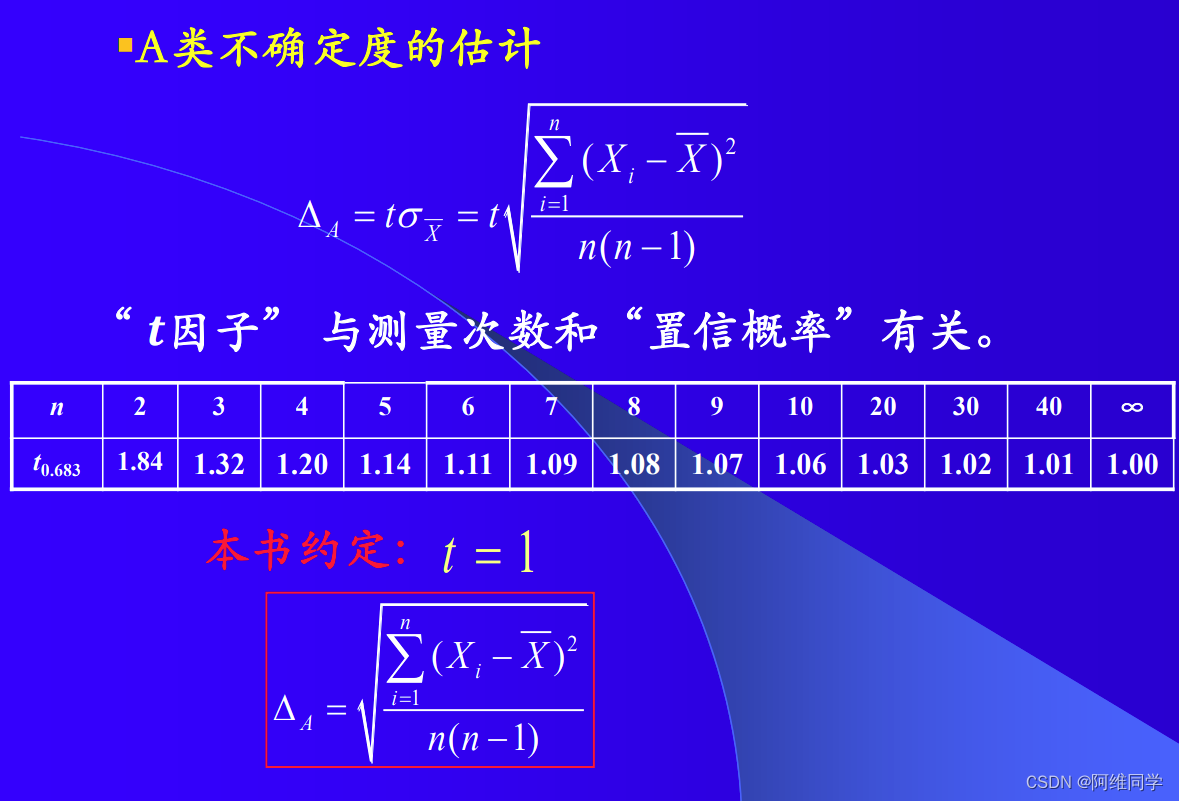
A类不确定度的计算方法

A类不确定度的计算方法通常基于贝塞尔公式（Bessel's formula）或标准偏差（standard deviation）的估计。以下是详细的计算步骤：

1. 进行多次独立重复测量：
   首先，在相同的测量条件下，对被测量进行多次（至少5次）独立重复测量。确保每次测量都是独立的，即每次测量之间不存在相互影响。

2. 计算测量结果的平均值：
   将所有测量结果相加，然后除以测量次数，得到测量结果的平均值（算术平均值）。

   公式为：(\bar{x} = \frac{1}{N} \sum_{i=1}^{N} x_i)

   其中，(\bar{x}) 是平均值，(N) 是测量次数，(x_i) 是第 (i) 次的测量结果。

3. 计算测量结果的偏差：
   对于每次测量，计算其与平均值的偏差（残差）。

   公式为：(d_i = x_i - \bar{x})

   其中，(d_i) 是第 (i) 次测量的偏差。

4. 计算偏差的平方和：
   将所有偏差的平方相加。

   公式为：(\sum_{i=1}{N} d_i2)

5. 计算A类不确定度：
   将偏差的平方和除以测量次数减一（(N-1)），然后取平方根，得到A类不确定度（标准偏差）。

   公式为：(s = \sqrt{\frac{1}{N-1} \sum_{i=1}{N} d_i2})

   其中，(s) 是A类不确定度（标准偏差）。

6. 自由度：
   在A类不确定度的计算中，自由度（degrees of freedom）是一个重要的参数，它等于测量次数减一（(N-1)）。

以下是一个Python代码示例，用于计算A类不确定度（标准偏差）：

import math  
  
# 假设这是你的测量数据列表  
measurements = [10.1, 10.2, 9.9, 10.0, 10.3]  
  
# 计算平均值  
mean = sum(measurements) / len(measurements)  
  
# 计算偏差的平方和  
sum_of_squared_deviations = sum((x - mean) ** 2 for x in measurements)  
  
# 计算A类不确定度（标准偏差）  
standard_deviation = math.sqrt(sum_of_squared_deviations / (len(measurements) - 1))  
  
# 输出结果  
print(f"平均值: {mean}")  
print(f"A类不确定度（标准偏差）: {standard_deviation}")

 B类不确定度

 

 间接测量结果不确定度的合成

 

 

间接测量结果不确定度的合成是指将所有影响间接测量结果的不确定度分量综合起来，得到一个总的不确定度。这个过程涉及到对不确定度分量的量化、合成以及最终的不确定度表达。

间接测量结果的不确定度合成涉及到误差传递的问题，即如何从一系列直接测量量的不确定度来评估最终间接测量结果的不确定度。这里介绍一种常用的合成方法——方和根合成法。

假设我们有一个间接测量量 \( Y = f(X_1, X_2, \ldots, X_n) \)，其中 \( X_i \) 是直接测量量，\( f() \) 是包含这些直接测量量的函数。我们已经知道了每个直接测量量 \( X_i \) 的不确定度 \( \Delta X_i \)。

首先，需要计算间接测量量 \( Y \) 对于每个直接测量量 \( X_i \) 的偏导数，然后利用这些偏导数来评估间接测量量的不确定度 \( \Delta Y \)。

具体步骤如下：

1. 计算间接测量量 \( Y = f(X_1, X_2, \ldots, X_n) \) 对每个直接测量量 \( X_i \) 的偏导数 \( \frac{\partial Y}{\partial X_i} \)。

2. 计算每个 \( \frac{\partial Y}{\partial X_i} \) 的不确定度 \( \Delta \frac{\partial Y}{\partial X_i} \)。这个值可以通过链规则来得到：

   \( \Delta \frac{\partial Y}{\partial X_i} = \frac{\partial Y}{\partial X_i} \cdot \frac{\Delta X_i}{X_i} \)。

3. 合成 \( \Delta Y \) 的平方：

   \( (\Delta Y)^2 = \sum_{i=1}^{n} \left( \frac{\partial Y}{\partial X_i} \cdot \frac{\Delta X_i}{X_i} \right)^2 \)。

4. 求出 \( \Delta Y \) 的值：

   \( \Delta Y = \sqrt{(\Delta Y)^2} \)。

这样，我们就得到了间接测量结果 \( Y \) 的不确定度 \( \Delta Y \)。注意，这里的 \( \Delta Y \) 是合成的标准差，它代表了由于各个直接测量量的不确定性所带来的综合影响。

在实际应用中，可能还需要考虑其他因素，例如非线性效应、相关性等，这会使得不确定度的合成变得更加复杂。不过，对于许多简单的情况，上述方法是足够使用的。

 这也太难了吧：

我们可以编写一个函数来执行间接测量结果的不确定度合成。但是，需要注意的是，通常我们不会直接计算偏导数的不确定度（(\Delta \frac{\partial Y}{\partial X_i})），而是直接使用偏导数和直接测量量的不确定度来合成间接测量结果的不确定度。

以下是一个Python函数示例，它接受一个函数f（表示间接测量量与直接测量量之间的关系）、一个包含直接测量量值的列表x_values以及一个包含直接测量量不确定度的列表delta_x_values，然后返回间接测量结果的不确定度delta_y：

⬇️⬇️⬇️

import numpy as np  
  
def propagate_uncertainty(f, x_values, delta_x_values):  
    # 计算偏导数（这里假设f是一个可微分的函数，我们使用numpy的梯度近似）  
    def numerical_gradient(f, x):  
        h = 1e-7  # 选择一个小的步长  
        grad = np.zeros_like(x)  
        it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])  
        while not it.finished:  
            ix = it.multi_index  
            old_value = x[ix]  
            x[ix] = old_value + h  
            fxh1 = f(x)  
            x[ix] = old_value - h  
            fxh2 = f(x)  
            grad[ix] = (fxh1 - fxh2) / (2 * h)  
            x[ix] = old_value  # 还原值以用于下一次迭代  
            it.iternext()  
        return grad  
  
    # 计算间接测量量的值  
    y_value = f(x_values)  
      
    # 计算间接测量量的不确定度  
    grad = numerical_gradient(f, x_values)  
    delta_y_squared = sum((grad[i] * delta_x_values[i] / x_values[i])**2 for i in range(len(x_values)))  
    delta_y = np.sqrt(delta_y_squared)  
      
    return delta_y  
  
# 示例：计算 Y = X1 + X2 的不确定度，其中 X1 = 10 (± 0.1), X2 = 20 (± 0.2)  
def f(x):  
    return x[0] + x[1]  
  
x_values = np.array([10, 20])  
delta_x_values = np.array([0.1, 0.2])  
  
delta_y = propagate_uncertainty(f, x_values, delta_x_values)  
print(f"Indirect measurement uncertainty: {delta_y}")

 对数微分法

 

 

对数微分法是在处理某些特定函数（如幂函数或多项积函数）时，通过求函数的对数导数来简化求导过程的一种方法。

1. 求对数导数：
   • 对函数f取对数，然后求导，得到的对数导数可以方便地转化为原函数的导数。
2. 利用链式法则：
   • 对数微分法依赖于链式法则和对数的性质，将复杂的乘积或幂函数转化为和或差的形式，从而简化求导过程。
3. 应用于不确定度计算：
   • 在间接测量值的不确定度计算中，当函数关系复杂时，可以使用对数微分法来简化计算过程。具体做法是先将函数转化为对数形式，然后应用全微分公式和链式法则来计算不确定度。

使用sympy库来处理符号计算，包括函数的对数导数、全微分以及不确定度的计算。以下是一个使用sympy来演示对数微分法以及如何将其应用于不确定度计算的例子。

首先，需要安装sympy库（如果你还没有安装的话）：

pip install sympy

 Python代码来演示对数微分法：

import sympy as sp  
  
# 定义变量  
x1, x2, x3 = sp.symbols('x1 x2 x3')  
uc_x1, uc_x2, uc_x3 = sp.symbols('uc_x1 uc_x2 uc_x3', real=True, positive=True) # 变量为正实数  
  
# 假设的复杂函数（例如多项积函数）  
f = x1**2 * x2 * sp.exp(x3)  
  
# 对数微分法  
# 对函数取对数  
log_f = sp.log(f)  
  
# 对对数函数求导  
diff_log_f_x1 = sp.diff(log_f, x1)  
diff_log_f_x2 = sp.diff(log_f, x2)  
diff_log_f_x3 = sp.diff(log_f, x3)  
  
# 转换为原函数的导数（链式法则）  
df_dx1 = f * diff_log_f_x1  
df_dx2 = f * diff_log_f_x2  
df_dx3 = f * diff_log_f_x3  
  
# 现在，假设我们要计算不确定度  
# 假设直接测量值的不确定度是已知的  
# 使用全微分公式计算合成不确定度  
du_f = sp.sqrt(  
    (df_dx1.subs({x1: 1, x2: 1, x3: 1}) * uc_x1)**2 +  
    (df_dx2.subs({x1: 1, x2: 1, x3: 1}) * uc_x2)**2 +  
    (df_dx3.subs({x1: 1, x2: 1, x3: 1}) * uc_x3)**2  
)  
  
# 打印结果  
print(f"df/dx1 = {df_dx1}")  
print(f"df/dx2 = {df_dx2}")  
print(f"df/dx3 = {df_dx3}")  
print(f"The combined uncertainty is: {du_f}")  
  
# 注意：在实际应用中，x1, x2, x3的值将不会是1，而是你测量或估计的值。  
# 这里为了简化计算，我们假设了x1=x2=x3=1。

 定义了一个复杂的函数f，然后使用对数微分法来找到它的导数。

接着，利用全微分公式来计算合成不确定度，这里假设了x1=x2=x3=1和相应的不确定度uc_x1, uc_x2, uc_x3。在实际情况中，需要将x1, x2, x3替换为实际的测量值。

 休息