扩散c++（floyd和Kruskal+并查集）

扩散

题目描述

一个点每过一个单位时间就会向四个方向扩散一个距离，如图。

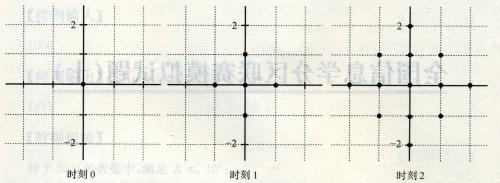
两个点a、b连通，记作e(a,b),当且仅当a、b的扩散区域有公共部分。连通块的定义是块内的任意两个点u、v都必定存在路径e(u,a0),e(a0,a1),…,e(ak,v)。给定平面上的n给点，问最早什么时刻它们形成一个连通块。

输入格式

第一行一个数n，以下n行，每行一个点坐标。

【数据规模】

对于20%的数据，满足1≤N≤5; 1≤X[i],Y[i]≤50;

对于100%的数据，满足1≤N≤50; 1≤X[i],Y[i]≤10^9。

输出格式

一个数，表示最早的时刻所有点形成连通块。

样例 #1

样例输入 #1

2
0 0
5 5

样例输出 #1

5

Floyd算法的解题过程

简单思考方式的所需时间（没有中转点干扰）

struct node{
	int a,b;
};//a，b代表的是x坐标和y坐标
inline int calc(node x,node y)
{
	int m=abs(x.a-y.a);
	int n=abs(x.b-y.b);
	return ceil((m+n)/2.0);
}

m表示的是横坐标之间的距离，n表示的是纵坐标之间的距离，m+n表示的是扩散的两点间的距离，但因为是同时扩散，扩散时间要 / 2（注意ceil向上取整，不考虑0.5s）

for(int i=1;i<=n;i++)
	   for(int j=1;j<=n;j++)
	   {
	   		int tep=calc(a[i],a[j]);
	   		dis[i][j]=tep;
	   }

我们用d i s [ i ] [ j ]来储存从 i 点到 j 点扩散所需要的时间，我们对点阵上任意两点间扩散所用的时间进行初始化

核心代码：

for(int k=1;k<=n;k++)
	   	    for(int i=1;i<=n;i++)
	   	    	for(int j=1;j<=n;j++)
	   	    		dis[i][j]=min(max(dis[i][k],dis[k][j]),dis[i][j]);

代码注释：

思路：

我们可以想到，扩散的过程中两个点之间如果有一个点在同时扩散的话，效率会比只有两个点在扩散快很多，那么由此可以我们可以把这个设想的点定义为k，那么从开始 i 扩散到中点 k 的时间可以记为d i s [ i , k ] ,从 k 扩散到结束点 j 的时间可以记为d i s [ k , j ] ，如此一来因为我们无法确定 i 到 k 的距离与 k 到 j 的距离谁更大一点，所以由此得到初步公式：
$$max(dis[i][k],dis[k][j])$$
我们确定了有中转站的路径所需的时间。不过这时也就有一个问题：因为我们是用for循环枚举的k，所以也就有d i s [ i ] [ j ]的距离更短的现象，由此得到最终的公式：
$$dis[i][j]=min(max(dis[i][k],dis[k][j]),dis[i][j])$$
*需要注意的是，因为要枚举到每个k 所以k层循环在最外面。

思考的奇怪问题：

1
问：我们枚举了每个k作为中转站，那么假如数据只有两个点，k不存在怎么办呢？？
答：我们枚举k时范围是到n，如果只有两个点，那么k枚举的范围也就只有两个点的范围，我们的方程只是将他自己与自己进行比较，因此不存在特判。
2
问：我们每次只枚举一个k的情况，那么当两点之间有两个k的时候怎么办呢？？？
答：我们设这四个点为 i ， j ， a ，b ，但根据我们的方程，我们会先枚举 i a，找到其最短路（最小时间）后，把这个时间储存下来，再枚举 j b 因此不用担心有多个中转站的情况。

最终代码

#include<bits/stdc++.h>
using namespace std;
struct node{
	int a,b;
};
node a[1000];
istream &operator >> (istream& in,node& x){
	in>>x.a>>x.b;
	return in;
}//运算符重载
inline int calc(node x,node y)
{
	int m=abs(x.a-y.a);
	int n=abs(x.b-y.b);
	return ceil((m+n)/2.0);
}
int n,dis[1000][1000];
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	   cin>>a[i];
	for(int i=1;i<=n;i++)
	   for(int j=1;j<=n;j++)
	   {
	   		int tep=calc(a[i],a[j]);
	   		dis[i][j]=tep;
	   }
	   for(int k=1;k<=n;k++)
	   	    for(int i=1;i<=n;i++)
	   	    	for(int j=1;j<=n;j++)
	   	    		dis[i][j]=min(max(dis[i][k],dis[k][j]),dis[i][j]);
	int ans=-1000000;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		   	ans=max(ans,dis[i][j]);//最后要找出其中时间最长的最为代表时间
	cout<<ans;
	return 0;
}

Kruskal+并查集做法

本题大致思路：

我们可以把它看成是图上的最短路问题，按Kruskal的思路，我们从最小的路开始找起（则两点之间扩散最短的路），直到所有的点形成连通块*（这个过程我们用到并查集），我们得到的两点扩散最长时间即为在这个过程中所需的最短时间。

最小的路：

inline int calc(node x,node y)
{
	int c=abs(x.a-y.a),d=abs(x.b-y.b);
	return ceil((c+d)/2.0);//向上取整
}

首先我们依然来求每个点之间的之间的距离

for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			if(i==j)continue;
			int tmp=calc(q[i],q[j]);
			u[cnt]=i;v[cnt]=j;w[cnt]=tmp;r[cnt]=cnt;
			cnt++;
		}

我们依次遍历每个点，找到每条路的权值 tmp ,我们把每条路的起点用u表示，每条路的终点用v表示，然后用w数组把每条边的权值储存下来，r记录w的序号（或位置），那么就得到了图上每两点之间的距离。

int cmp(int a,int b)
{
	return w[a]<w[b];
}
sort(r,r+cnt,cmp);

这里是间接排序，我们利用w的值来排r的顺序，在后续的调用中用r来指代w，如r [ i ]，我们就知道这是第i小的w的位置。（其实可以直接w，相对容易理解且更加简单）

并查集

for(int i=1;i<=n;i++)
	    p[i]=i;//将每个点的根节点初始化为它本身
int find(int a)
{
	if(p[a]!=a) p[a]=find(p[a]);//如果根节点不是他本身的话，我们就继续查找根节点，并更新总根节点
	return p[a];//直到找到根节点之后返回根节点的值
}
int ans;
	for(int i=1;i<=cnt-1;i++)
	{
		int q=r[i];
		int x=find(u[q]),y=find(v[q]);
		if(x!=y) 
		{
			p[x]=y;
			ans=w[q];
		}
	}

find函数用于将两个集合合并到一起，for循环将不断的合并集合，更新根节点，并且ans储存所需的时间（因为是从最小边开始的所以最后直接输出ans即可

思考的奇怪问题

if(x!=y) 
		{
			p[x]=y;
			ans=w[q];
		}

在这一段代码中，我们如果将他更新为：

if(x!=y) 
		{
			p[u[q]]=y;
			ans=w[q];
		}

那么我们将收获wa代码
在并查集中，需要注意的是更新根节点时候更新的是一整个集合的总根节点，如果写为第二段代码的样子，更新的只是u[p]的根节点，等于在这个集合中只改变了一个小分支，所以是错误的。

最终代码：

#include<bits/stdc++.h>
using namespace std;
int n;
struct node{
	int a,b;
};
node q[1000];
istream &operator >> (istream& in,node& x){
	in>>x.a>>x.b;
	return in;
}
inline int calc(node x,node y)
{
	int c=abs(x.a-y.a),d=abs(x.b-y.b);
	return ceil((c+d)/2.0);
}
int p[100000],u[100000],v[100000],w[100000],r[100000];
int cmp(int a,int b)
{
	return w[a]<w[b];
}
int find(int a)
{
	if(p[a]!=a) p[a]=find(p[a]);
	return p[a];
}
int main()
{
	int cnt=0;
	cin>>n;
	for(int i=1;i<=n;i++)
	   cin>>q[i];
	for(int i=1;i<=n;i++)
	    p[i]=i;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			if(i==j)continue;
			int tmp=calc(q[i],q[j]);
			u[cnt]=i;v[cnt]=j;w[cnt]=tmp;r[cnt]=cnt;
			cnt++;
		}
	sort(r,r+cnt,cmp);
	int ans;
	for(int i=1;i<=cnt-1;i++)
	{
		int q=r[i];
		int x=find(u[q]),y=find(v[q]);
		if(x!=y) 
		{
			p[x]=y;
			ans=w[q];
		}
	}
	cout<<ans;
	return 0;
}