【离散数学】图的基本概念

通路和回路

初级：不同点

简单：不同边

连通图

点割集

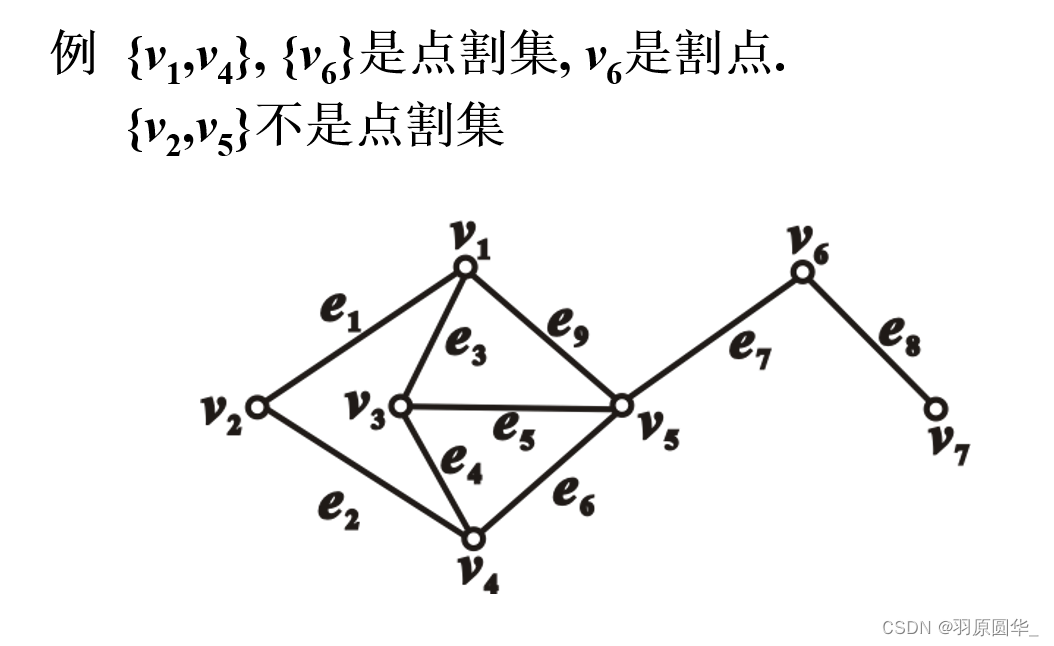
 ∵P【G-v5】= P【G-{v2，v5}】

∴{v2，v5}不是点割集

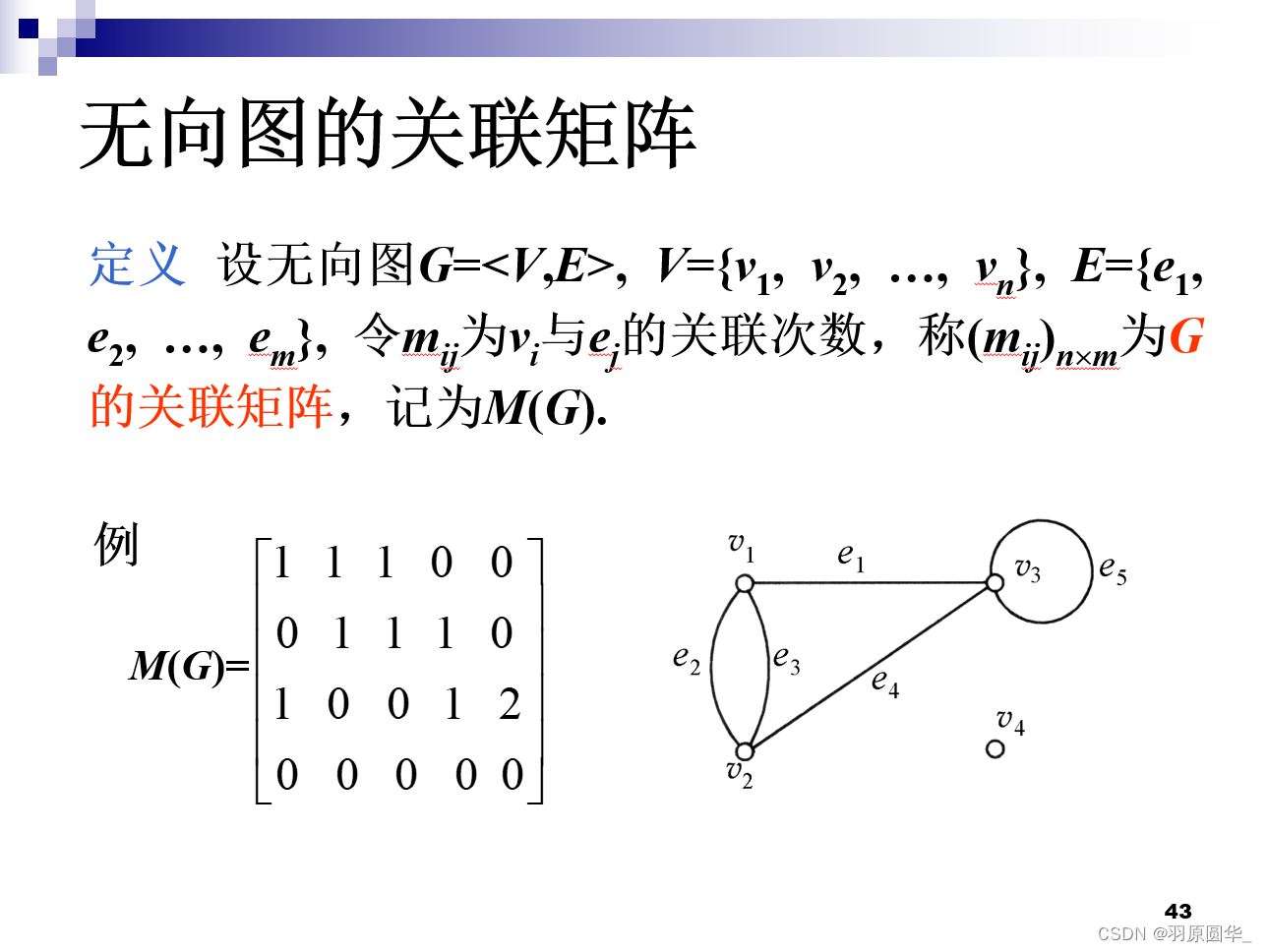
图的矩阵表示

关联矩阵：点和边

行是点，列是边

 

邻接矩阵：点和点

邻接矩阵求通路和回路

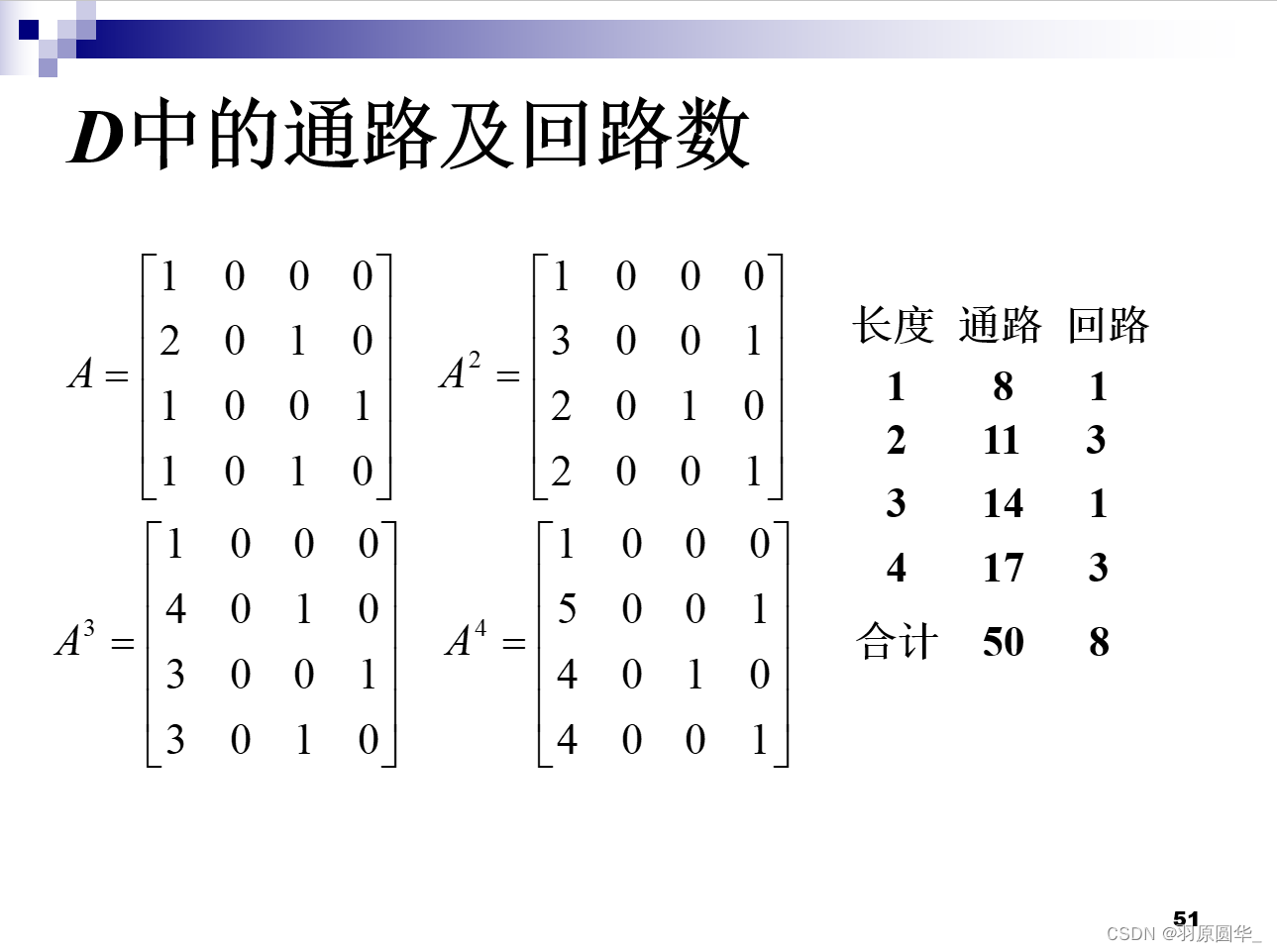
矩阵的平方计算

 

可达矩阵

两点是否可达 

最短路

迪杰斯特拉，每轮找一个最近的点对周围的点进行松弛，本质是贪心思维

*标星号的是下一轮遍历的中心点

着色

 应用

有 n项工作, 每项工作需要一天的时间完成. 有些工作由于需要相同的人员或设备因而不能同时进行, 问至少需要几天才能完成所有的工作?

用顶点表示工作，如果两项工作不能同时进行就用一条边连接对应的顶点。则工作的时间安排就对应于这个图的点着色：着同一种颜色的顶点对应的工作可以安排在同一天，所需的最少天数即为该图的色数。

计算机有 k个寄存器, 现正在编译一个程序, 要给每一个变量分配一个寄存器. 如果两个变量要在同一时刻使用, 则不能把它们分配给同一个寄存器.如何给变量分配寄存器?

此问题也可以转化为图的点着色问题：每个变量对应一个顶点，如果两个变量在同一时刻使用，则用一条边连接这两个变量。于是，这个图的色数即对应所需寄存器的数量：给同一种颜色的变量分配同一个寄存器是安全的。

【例】 学生会下设6个委员会, 第一委员会={张, 李, 王}, 第二委员会={李, 赵, 刘}, 第三委员会={张, 刘, 王}, 第四委员会={赵, 刘, 孙}, 第五委员会={张, 王}, 第六委员会={李, 刘, 王}. 每个月每个委员会都要开一次会, 为了确保每个人都能参加他所在的委员会会议, 这6个会议至少要安排在几个不同时间段?

将委员会化为图的点，将有人员冲突的委员会用用一条边连接，再次转化为图的点着色问题

总结

         图着色问题的应用主要是将问题抽象成对立的点，用着色法解决；