线段树（查询+求区间和、最值+单点、区间修改）

线段树的查询：假如需要查询区间为[x，y]，若区间[l，r]满足x<=l<=r<=y，则该区间已被完全覆盖，可直接返回该区间的权值或最大值，否则递归向下查找。

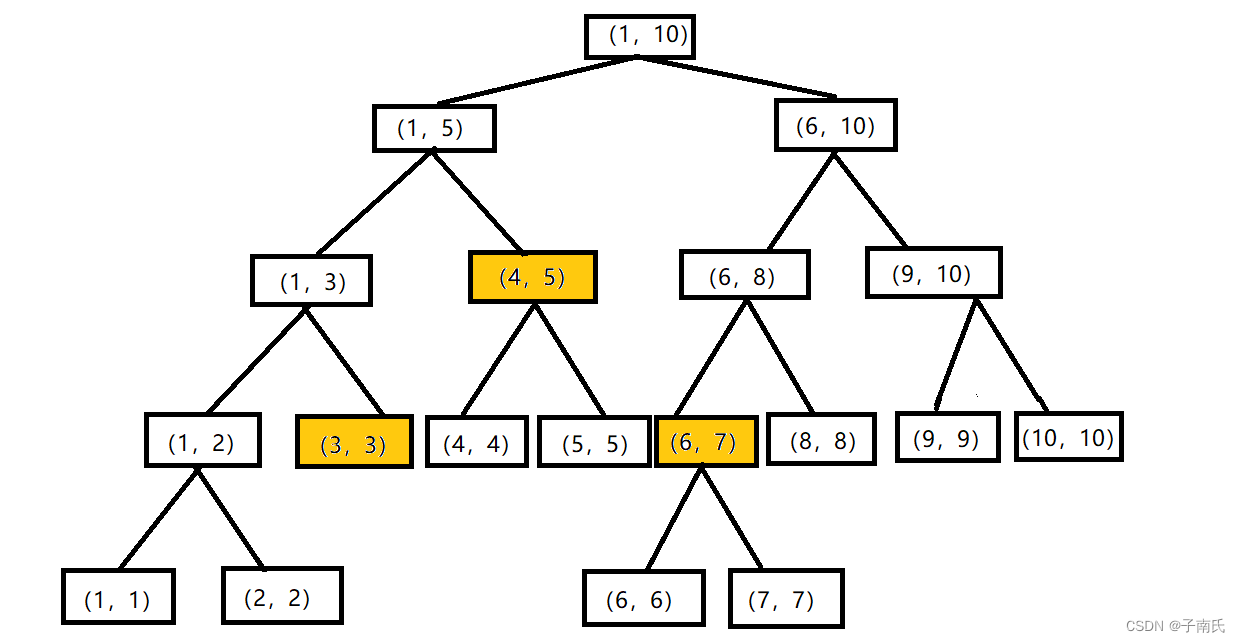
 例如查询[3，7]的区间和或最大值，由例图可知，直接返回[3，3]，[4，5]，[6，7]的总和即可，不必查询到[4，4]，[5，5]的值。

据此思想，可写

if (T[u].l == T[u].r && T[u].l == i) {   //找出叶子结点
		T[u].sum += v;
		T[u].Max += v;
}
else{
   递归……
}

递归时根据二叉树的特点，左孩子下标为父节点*2，右孩子下标为父节点*2+1，然后在左子树和右子树中分别递归。

下面是求区间和，单点修改，求最值的代码（附详细注释）——

输入：                   输出：
10 5                     26
3 2 4 5 6 8 1 2 3 7      8
1 1 5                    37
2 3 8                  
1 7 3
3 4 9
2 1 7

#include <iostream>
#include <algorithm>
#include <limits.h>
using namespace std;
const int n = 1000;
int N, M;          //总数与执行次数
int value[n];      //权值
typedef struct TNode {
	int l, r;      //左区间，右区间
	int sum, Max;  //权值，最大值
}Tree[4 * n];
Tree T;
void pushup(int u) {   //点更新  
	T[u].sum = T[u << 1].sum + T[u << 1 | 1].sum;
}
void build(int u, int l, int r) {    //建立线段树
	if (l == r) {
		T[u] = { l,r,value[l],value[l] };//因为叶子节点权值与最大值相同，所以直接赋值value[]
	}
	else {
		T[u] = { l,r };
		int mid = (l + r) >> 1;
		build(u << 1, l, mid);          //左子树递归建立
		build(u << 1 | 1, mid + 1, r);  //右子树递归建立
		pushup(u);                      //更新结点的权值
		T[u].Max = max(T[u << 1].Max, T[u << 1 | 1].Max); //更新结点的最大值
	}
}
void modify(int u, int i, int v) {    //单点修改
	if (T[u].l == T[u].r && T[u].l == i) {   //找到叶子结点直接修改
		T[u].sum += v;
		T[u].Max += v;
	}
	else {
		//如果该结点不是叶子结点，则开始递归往下查询
		int mid = (T[u].l + T[u].r) >> 1;
		if (i <= mid) {
			modify(u << 1, i, v);   //左子树中递归
		}
		else {
			modify(u << 1 | 1, i, v);   //右子树中递归
		}
		//记得修改权值与最大值
		pushup(u);
		T[u].Max = max(T[u << 1].Max, T[u << 1 | 1].Max);
	}
}
int query_sum(int u, int a, int b) { //区间求和
	if (a <= T[u].l && T[u].r <= b) {   //如果区间覆盖，可直接返回该区间的权值
		return T[u].sum;
	}
	else {
		//如果没有覆盖，则递归往下
		int sum = 0;
		int mid = (T[u].l + T[u].r) >> 1;
		if (a <= mid) {
			sum += query_sum(u << 1, a, b);
		}
		if (b > mid) {
			sum += query_sum(u << 1 | 1, a, b);
		}
		return sum;
	}
}
int query_Max(int u, int a, int b) { //区间求最大值，（求最大值与求和类似）
	if (a <= T[u].l && T[u].r <= b) { //已经是叶子节点
		return T[u].Max;
	}
	else {
		int mid = (T[u].l + T[u].r) >> 1;
		int MAX = INT_MIN;  //要求最大值，则需设一个最小值来比较
		if (a <= mid) {
			MAX = max(MAX, query_Max(u << 1, a, b));
		}
		if (b > mid) {
			MAX = max(MAX, query_Max((u << 1) | 1, a, b));
		}
		return MAX;
	}
}
int main() {    //主函数
	cin >> N >> M;
	for (int i = 1; i <= N; i++) {
		cin >> value[i];
	}
	build(1, 1, N);  //建树
	int k, a, b;
	for (int i = 0; i < M; i++) {
		cin >> k >> a >> b;
		if (k == 1) {      //1-单点修改
			modify(1, a, b);
		}
		if (k == 2) {     //2-求区间和
			cout << query_sum(1, a, b) << endl;
		}
		if (k == 3) {     //3-求区间最大值
			cout << query_Max(1, a, b) << endl;
		}
	}
	return 0;
}

区间修改：即修改所给区间[l，r]内所有的叶子结点的值，如果将区间拆分成（r-l+1）个单点修改，则算法的复杂度过高，我们可以尝试像区间查询一样，先把区间分成线段树上的若干个区间，然后分别修改这几个区间。

 例如我们要修改[3，7]的区间，仅需要修改[3，3]，[4，5]，[6，7]即可，如果查询不到[4，4]，[5，5]两个单点时，它们可以不用修改，只要在其父节点[4，5]上做个标记，待需要时将标记下放到左右孩子上，就可以修改子树里的值。

由于这种偷懒行经，我们称呼这种标记为懒标记。

对于标号为x的区间[l，r]，其左右孩子区间分别为[l，mid]，[mid+1，r]【 mid=(l+r)/2 】。

若设置[l，r]的懒标记为：lazy[x]，那么值：sum[x]=lazy[x]*(l-r+1).【这是因为区间所加值=该区间下所有结点累加值的总和，比如[4，5]区间，需要2*lazy】。

那么左右孩子：

lazy[2*x]+=lazy[x]，sum[2*x]+=lazy[x]*(mid-l+1)

lazy[2*x+1]+=lazy[x]，sum[2*x+1]+=lazy[x]*(r-mid+1+1)

lazy[x]=0

此处是将父节点的标记下放到左右孩子上，并且将父节点的标志清空。

清空父节点的标志非常重要，否则运行到这一行会重复累加导致结果错误。

且懒标记与值的更新需要“+=”，这是为了防止下放标记时左右孩子本身就有懒标记

下面是洛谷例题与代码(附详细注释)，末尾附有原题链接——

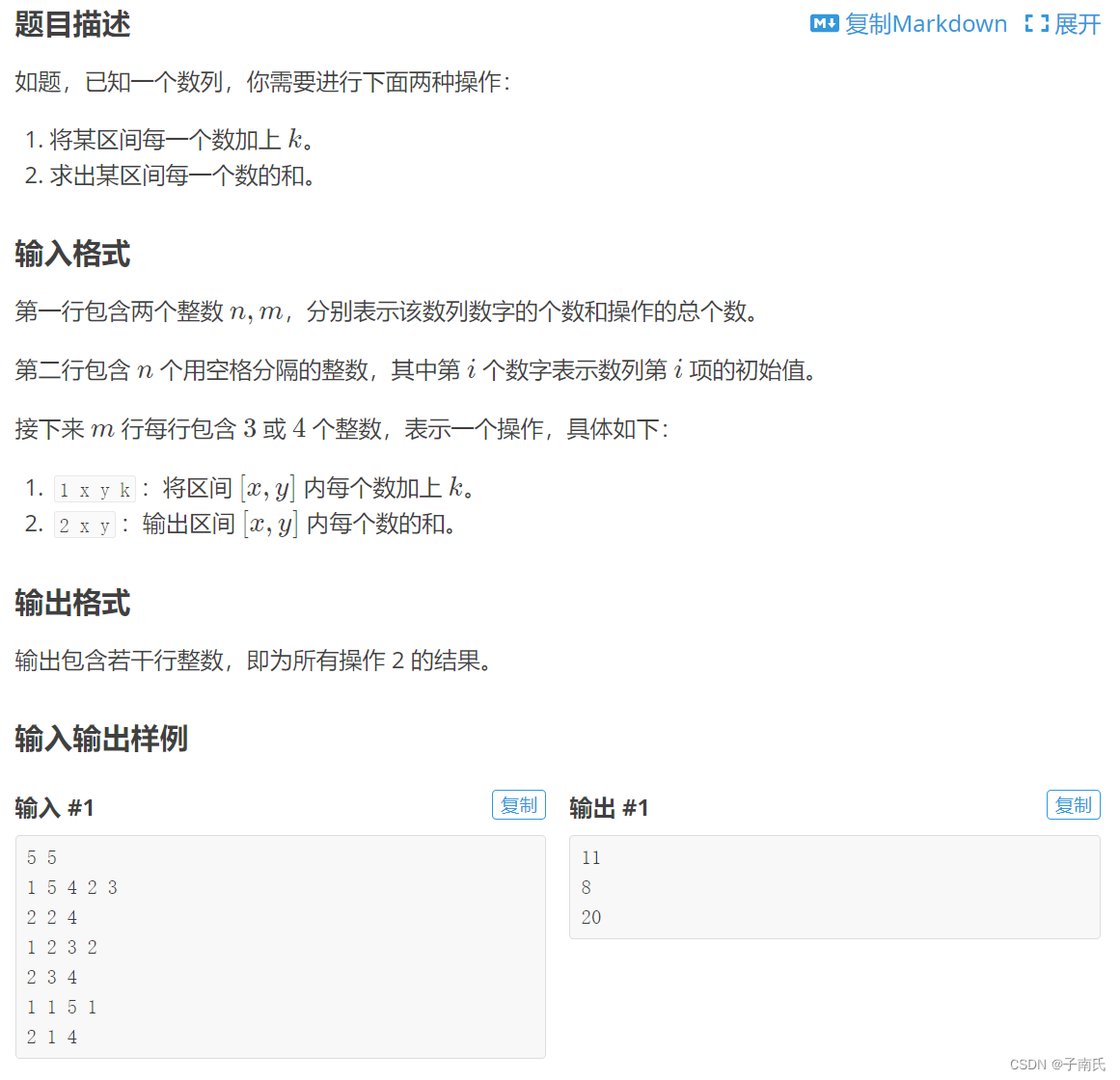
#include <iostream>
#include <algorithm>
using namespace std;
const int n = 100010;
int value[n], N, M;
typedef struct TNode {
	int l, r;
	long long lazy, sum;     //左区间，右区间，懒标记，节点总和
}Tree[4 * n];
Tree T;
//点更新
void pushup(int u) {         
	T[u].sum = T[u << 1].sum + T[u << 1 | 1].sum;  //一个结点的值为其左右孩子值的总和
}
//懒标记向下传递
void pushdown(int u) {       
	if (T[u].lazy) {         //如果懒标记不为0，向下传递
		T[u << 1].lazy += T[u].lazy;   //将其懒标记下传给左子树，‘+=’为了防止该节点的左子树本身就有懒标记
		T[u << 1].sum += T[u].lazy * (T[u << 1].r - T[u << 1].l + 1);  //该左孩子的增加的值为其所有子节点增加的总和
		T[u << 1 | 1].lazy += T[u].lazy;   //右子树同样
		T[u << 1 | 1].sum += T[u].lazy * (T[u << 1 | 1].r - T[u << 1 | 1].l + 1);
		T[u].lazy = 0;     //此时应把该节点的标记清零
	}
}
//建立线段树
void build(int u, int l, int r) {          
	if (l == r) {
		T[u] = { l,r,0,value[l]};       //懒标记初始值为0
	}
	else {
		T[u] = { l, r, 0 };
		int mid = (l + r) >> 1;
		build(u << 1, l, mid);          //递归建立左子树
		build(u << 1 | 1, mid + 1, r);  //递归建立右子树
		pushup(u);
	}
}
//区间修改
void update(int u, int l, int r, int k) {   
	if (l <= T[u].l && T[u].r <= r) {     //区间覆盖     
		T[u].sum += (long long)k * (T[u].r - T[u].l + 1);
		T[u].lazy += k;   //防止该节点本身有懒标记
	}
	else {
		pushdown(u);
		int mid = (T[u].l + T[u].r) >> 1;
		if (l <= mid) {
			update(u << 1, l, r, k);
		}
		if (r > mid) {
			update(u << 1 | 1, l, r, k);
		}
		pushup(u);
	}
}
//区间求和
long long query(int u, int l, int r) {          
	if (l <= T[u].l && T[u].r <= r) {     //区间覆盖     
		return T[u].sum;
	}
	else {
		pushdown(u);
	    long long sum = 0;
	    int mid = (T[u].l + T[u].r) >> 1;
	    if (l <= mid) {                       //左子树中递归查找
		sum += query(u << 1, l, r);
	    } 
	    if (r > mid) {                        //右子树中递归查找
		sum += query(u << 1 | 1, l, r);
	    }
	    return sum;
	}
}
//主函数
int main() {            
	scanf("%d %d", &N, &M);
	for (int i = 1; i <= N; i++) {
		scanf("%d", &value[i]);
	}
	build(1, 1, N);     //建树
	int f, l, r, k;
	while (M--) {
		scanf("%d", &f);
		if (f == 1) {   //区间修改
			scanf("%d %d %d", &l, &r, &k);
			update(1, l, r, k);
		}
		if (f == 2) {   //区间求和
			scanf("%d %d", &l, &r);
			printf("%lld\n", query(1, l, r));
		}
	}
	return 0;
}

 https://www.luogu.com.cn/problem/P3372