原神中关于C语言的基本算法-二分查找（带代码）

当你的好朋友叫你一起来当op的时候

你-会不会犹豫呢？？你会不会想要和他一起玩呢？玩就对了！超！原神这么好玩，一定要玩的！！这是正确的！！

所以，你一定要去加他的UID然后一起来当op哈哈哈。

那么，你有没有想过？

只要输入他的UID，就会准确的弹出好朋友的UID，一点都不带差的（哈哈，有点废话）

所以，初步当程序员你，会不会想过，这些（原神/王者)类大型游戏中这种最简单的去（搜索ID查找到好友)的基本算法原理是怎么实现的呢？

那就跟着雷电将军来看一看

 不得不说！是真的👍🏻

咳咳，好了，步入正题

在搜索UID添加好友的基本流程操作中

让我们看到了一个最简单的程序设计，二分查找！！！对，也就是折半查找！相对于暴力查找效率高了一半！

二分查找的基本算法概念

• 二分法(折半查找）是一个查找算法
• 要求：数据必须是有序列表
• 核心思想：掐头结尾取中间
• 初始条件：left = 0, right = length - 1
• 终止条件：left > right
• 向左查找：right = mid - 1
• 向右查找：left = mid + 1
• 折半查找法：一种实现二分查找的高级方法
• 查找条件需要访问元素的直接右邻居
• 使用元素的右邻居来确定是否满足条件，并决定是向左还是向右
• 保证查找空间在每一步中至少有2个元素
• 需要进行后处理。当你剩下1个元素的时候，循环/递归结束，需要评估剩余元素是否满足条件
• 折半查找法 也称为二分查找法，它充分利用了元素间的次序关系，采用分治策略，可在最坏的情况下用O(log n)完成搜索任务。它的基本思想是：（这里假设数组元素呈升序排列）将n个元素分成个数大致相同的两半，取a[n/2]与欲查找的x作比较，如果x=a[n/2]则找到x，算法终止；如 果x<a[n/2]，则我们只要在 数组 a的左半部继续搜索x；如果x>a[n/2]，则我们只要在数组a的右 半部继续搜索x.
• 

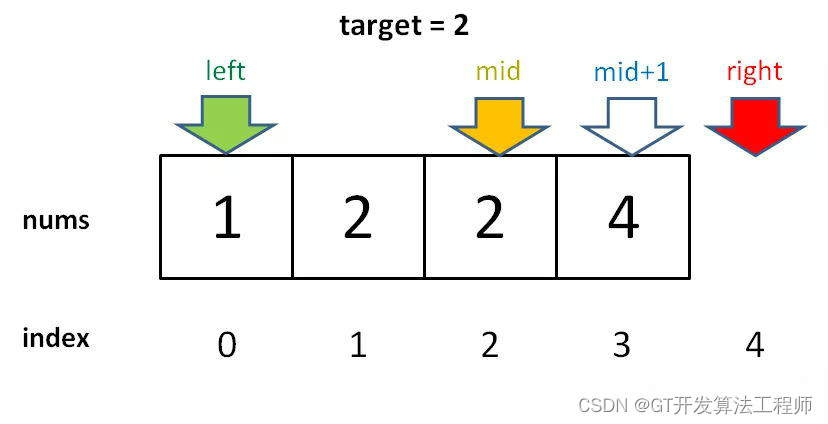
比如说查找第一个K 

就是根据元素下标去 找

 这样是不是更清楚了呢？

接下来代码演示一下：

二分查找（二分法查找在有序数组中查找具体的某个数字n）

下面是8种代码演示：

第一种：C语言/ C++代码演示

# include<stdio. h>

int main()

//二分法查找在有序数组中查找具体的某个数字n

{

        int arr[] = { 1,2,3,4,5,6,7,8,9,10 };

        int k = 7;//找7

        int sz = sizeof(arr) / sizeof(arr[0]);//计算元素个数

        int left = 0;//左下标

        int right = (sz - 1);//右下标

        while (left <= right)

        {

               int mid = (left + right) / 2;

               if (arr[mid] > k)//要是比要找的数字大，左下标不变，右下标减一

               {

                       right = mid - 1;

               }

               else if (arr[mid] < k)//要是比要找的数字小，右下标不变，左下标加一

               {

                       left = mid + 1;

               }

               else

               {

                       printf("找到了，下标为：%d\n", mid);

                       break;

               }

        }

        if (left > right)

        {

               printf("找不到\n");

        }

        return 0;

}

C语言/ C++第二种方法演示：

int bsearchWithoutRecursion(int array[],int low,int high,int target)

{

    while(low<=high)

        {

            int mid=low+(high-low)/2;//还是溢出问题

            if(array[mid]>target)

                high=mid-1;

            else if(array[mid]<target)

            low=mid+1;

            else

                return mid;

        }

    return-1;

}

第二种：phython代码演示：

def bin_search(data_list, val):    

    low = 0 # 最小数下标    

    high = len(data_list) - 1 # 最大数下标    

    while low <= high:        

        mid = (low + high) // 2 # 中间数下标        

        if data_list[mid] == val: # 如果中间数下标等于val, 返回            

            return mid        

        elif data_list[mid] > val: # 如果val在中间数左边, 移动high下标            

            high = mid - 1        

        else: # 如果val在中间数右边, 移动low下标            

            low = mid + 1    

    return # val不存在, 返回None

ret = bin_search(list(range(1, 10)), 3)

print(ret)

第三种：PHP代码演示

function binsearch($x,$a){

    $c=count($a);

    $lower=0;

    $high=$c-1;

    while($lower<=$high){

        $middle=intval(($lower+$high)/2);

        if($a[$middle]>$x){

            $high=$middle-1;

        } elseif($a[$middle]<$x){

            $lower=$middle+1;

        } else{

            return $middle;

        }

    }

    return -1;

}

第四种：

JavaScript代码

var Arr = [3, 5, 6, 7, 9, 12, 15];
function binary(find, arr, low, high) {
    if (low <= high) {
        if (arr[low] == find) {
            return low;
        }
        if (arr[high] == find) {
            return high;
        }
        var mid = Math.ceil((high + low) / 2);
        if (arr[mid] == find) {
            return mid;
        } else if (arr[mid] > find) {
            return binary(find, arr, low, mid - 1);
        } else {
            return binary(find, arr, mid + 1, high);
        }
    }
    return -1;
}
binary(15, Arr, 0, Arr.length - 1);

第5种：C#代码演示

public static int Method(int[] nums, int low, int high, int target)

        {

            while (low <= high)

            {

                int middle = (low + high) / 2;

                if (target == nums[middle])

                {

                    return middle;

                }

                else if (target > nums[middle])

                {

                    low = middle + 1;

                }

                else if (target < nums[middle])

                {

                    high = middle - 1;

                }

            }

            return -1;

        }

第6种：

Go源代码

func binarySearch(checkSlice []int, findVal int) int {

    pos := -1

    left, right := 0, len(checkSlice)  //此处right长度不减1 ， 如果最大值为查找值，此处减一代码进入死循环

Loop:

    for {

        if(left >= right){
            break Loop
        }

        mid := (left + right) / 2

        switch true {

        case checkSlice[mid] < findVal :
            left = mid
        case checkSlice[mid] == findVal :
            pos = mid
            break Loop
        case checkSlice[mid] > findVal :
            right = mid

        }

    }

    return pos

}

第7种：Swift源代码演示

func binarySearch<T: Comparable>(_ a: [T], key: T) -> Int? {    

    var lowerBound = 0    

    var upperBound = a.count    

    while lowerBound < upperBound {        

        let midIndex = lowerBound + (upperBound - lowerBound) / 2        

        if a[midIndex] == key {            

            return midIndex        

        } else if a[midIndex] < key {            

            lowerBound = midIndex + 1        

        } else {            

            upperBound = midIndex        

        }    

    }    

    return nil

}

它的结构模型：

讲到这里的你，是不是还没听清呢？

那么，再次总结一下加深印象：

• 二分法(折半查找）是一个查找算法
• 要求：数据必须是有序列表
• 核心思想：掐头结尾取中间
• 初始条件：left = 0, right = length - 1
• 终止条件：left > right
• 向左查找：right = mid - 1
• 向右查找：left = mid + 1
• 折半查找法：一种实现二分查找的高级方法
• 查找条件需要访问元素的直接右邻居
• 使用元素的右邻居来确定是否满足条件，并决定是向左还是向右
• 保证查找空间在每一步中至少有2个元素
• 需要进行后处理。当你剩下1个元素的时候，循环/递归结束，需要评估剩余元素是否满足条件
• 折半查找法 也称为二分查找法，它充分利用了元素间的次序关系，采用分治策略，可在最坏的情况下用O(log n)完成搜索任务。它的基本思想是：（这里假设数组元素呈升序排列）将n个元素分成个数大致相同的两半，取a[n/2]与欲查找的x作比较，如果x=a[n/2]则找到x，算法终止；如 果x<a[n/2]，则我们只要在 数组 a的左半部继续搜索x；如果x>a[n/2]，则我们只要在数组a的右 半部继续搜索x.
•