台北房价数据分析-CSDN博客

这里我使用的数据集是台北房产数据集[1]，该数据集以xlsx的格式进行存储，共有414条记录，NA代表缺失数据，有6个解释变量，分别为：X1=交易年月、X2=房龄（单位：年）、X3=最近公交站距离（单位：米）、X4=附近便利店家数（整数）、X5=地理坐标纬度（单位：度）、X6=地理坐标经度（单位：度），被解释变量：Y=单位面积房价（每坪价格，新台币计，1坪=3.3平米）。

2.2数据集基本结构预览

这里使用Pandas读取得到的数据是Pandas特有的DataFrame数据格式，可以使用head和tail方法来查看数据的前10份和后10份。

代码如下：

data = pd.read_excel("台北房产数据集.xlsx")

data.head(10)

data.tail(10)

效果如下

2.3 输出数据集中变量的类型

通过dtypes来查看数据集中变量的类型。代码为data.dtypes,效果如下：

2.4 查看房龄和单位面积房价的关系

查看二者关系的代码如下：

fig, ax = plt.subplots()

ax.scatter(x=data["X2 房龄"], y=data["Y 单位面积房价"])

plt.ylabel("Y 单位面积房价",fontproperties=myfont, fontsize=13)

plt.xlabel("X2 房龄",fontproperties=myfont, fontsize=13)

plt.show()

效果如下：

从图显示的结果可以看出，房龄与单位面积房价大致呈线性负相关关系。也就是说，房龄越大，房价越低。此外，细心观察可以发现，上图中左上角有一个数据有点不正常，通常将这类点称之为异常值点。现在将其删除，并且再次画图。

# 删除异常值点

data_drop = data.drop(

    data[(data['Y 单位面积房价'] > 90)].index)

fig, ax = plt.subplots()

# 绘制散点图

ax.scatter(x=data_drop["X2 房龄"], y=data_drop["Y 单位面积房价"])

plt.ylabel("Y 单位面积房价",fontproperties=myfont, fontsize=13)

plt.xlabel("X2 房龄",fontproperties=myfont, fontsize=13)

plt.show()

plt.savefig(fname="房龄2.png",figsize=[10,10])

2.5 分析离散变量X4附近的便利店家数与单位面积房价的关系

上面主要画出的是房龄与单位面积房价的关系，而房龄和单位面积房价都是连续的数值，因比可以直接画出它们的关系。而在数据集中还存在另一种离散型特征，对于这类数据，可以通过箱线图进行画出。例如，在数据集中附近的便利店家数是一个离散型特征，现在画出该特征与单位面积房价的关系。

var = "X4 附近便利店家数"

data = pd.concat([data_drop["Y 单位面积房价"], data_drop[var]], axis=1)

# 画出箱线图

f, ax = plt.subplots(figsize=(8, 6))

fig = sns.boxplot(x=var, y="Y 单位面积房价", data=data)

fig.axis(ymin=0, ymax=80)

plt.savefig(fname="箱线图.png",figsize=[10,10])

从上图中可以看出，附近便利店家数越多，房价越高。

2.6 通过热图来分析所有特征之间的相关性以及与单位面积房价的关系

上面分析了单个特征与单位面积房价的关系，现在可以通过热力图来分析所有特征之间的相关性以及与单位面积房价的关系。由于序号一列仅仅为了表示数据的个数，无实际意义，现在将其删除。代码如下：

data_drop = data_drop.drop(columns="序号")

data_drop.head()

cm1 = data_drop.corr()

hm = sns.heatmap(cm1,cbar=True, annot=True, square=True, fmt='.2f')

plt.show()

从图中可以看出单位面积房价和距离公交车站的远近相关程度大，这也很符合常识，毕竟交通便利很重要。下面在画出这些特征之间的关系。

cols = ['Y 单位面积房价', 'X1 交易年月', 'X2 房龄',

        'X3 最近公交站距离', 'X5 纬度', 'X6 经度']

zd = sns.pairplot(data_drop[cols], size=2.5)

plt.show()

这三张图其实是一张图，都是用来分析各个特征之间的关系。

三数据清洗

3.1 分析单位面积房价的数据是否满足正态分布

单位面积房价也即是所要预测的列，这里先对其进行分析（其余的将在确定好特征列时分析）。使用describe方法查看数据的基本情况。data_drop['Y 单位面积房价'].describe()

这里由于删掉了一个异常值和一个单位面积房价缺失的值所以是412行。然后利用相关代码画出分布图。

from scipy.stats import norm, skew

data_drop1 = data_drop.drop(index=207)

sns.distplot(data_drop1['Y 单位面积房价'], fit=norm)

# 获得均值和方差

(mu, sigma) = norm.fit(data_drop1['Y 单位面积房价'])

print('\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))

# 画出数据分布图

plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],loc='best')

plt.ylabel('频率')

# 设置标题

plt.title('单位面积房价分布',fontproperties=myfont)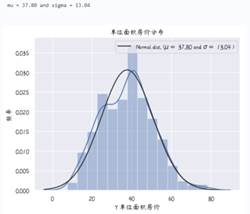

可以看到，该数据集貌似是常见的正态分布，即高斯分布。现在画出其Q-Q图

from scipy import stats

fig = plt.figure()

res = stats.probplot(data_drop1['Y 单位面积房价'], plot=plt)

plt.show()

从图上可以看出该列确实符合正态分布。

3.2 缺失值处理，利用多种补缺方式处理

使用相关函数查找数据集中的缺失值data_drop.isnull().sum().sort_values(ascending=False)

通过分析我发现该数据集存在两个缺失值。计算该数据的缺失率，代码如下

data_na = (data_drop.isnull().sum() / len(data))

data_na = data_na.drop(data_na[data_na == 0].index).sort_values(ascending=False)

missing_data = pd.DataFrame({'Missing Ratio': data_na})

这里我采用了三种方法来进行填充缺失值：

方法1：

#沿Y轴方向，进行填充选择前面的值

data1 = data_drop.fillna(axis=0,method='ffill')

方法2：

#沿Y轴方向，进行填充选择后面的值

data2 = data_drop.fillna(axis=0,method='bfill')

方法3：

data3 = data_drop.fillna(data_drop.mean())

在下文中我将使用data2做为数据进行操作。

3.3 特征提取

在数据集中，特征主要分为两种，分别是数值型特征和类别型特征。数值型特征就是连续数值组成的特征，例如房子的年龄；而类别型特征则是由两类或两类以上类别组成的特征，例如房子是否带周围的便利店，即包含是和否两个类别。

在数据集中有一些特征属于类别型特征，但却用数值来表示，例如交易年月。因此，要转换其成为类别型特征。

data2["X1 交易年月"] = data2["X1 交易年月"].apply(str)

接下来对类别型的特征列进行编码。将其转换成为用数值来表示的类别型特征。

from sklearn.preprocessing import LabelEncoder

lbl = LabelEncoder()

lbl.fit(list(data2["X1 交易年月"].values))

data2["X1 交易年月"] = lbl.transform(list(data2["X1 交易年月"].values))

data2["X1 交易年月"].head(10)

如下图所示

四数据整理

4.1 分析数据的特征列是否符合正态分布

在前文分析房子单位面积价格时，检测了其是否符合正态分布。这里这对数据集中的数值特征列进行同样的分析。先通过SciPy提供的接口scipy.stats.skew来判断其偏度。

numeric_feats = data2.dtypes[data2.dtypes != "object"].index

# 检测特征值

skewed_feats = data2[numeric_feats].apply(

    lambda x: skew(x.dropna())).sort_values(ascending=False)

print("\nSkew in numerical features: \n")

skewness = pd.DataFrame({'Skew': skewed_feats})

skewness.head(7)

从图上可知，各个特征列的偏度并未很大，因此代表着这些特征列都很接近正态分布，无需用额外的方法进行矫正。

4.2 将各特征列进行标准化

data2.apply(lambda x:(x-np.min(x))/(np.max(x)-np.min(x)))

4.3 根据数据清洗结果对数据集转化并生成新的数据集

data_y = data2['Y 单位面积房价']

data_X = data2.drop(['Y 单位面积房价'], axis=1)

data_X.shape,data_y.shape

结果为((413, 6), (413,))

4.4 数据集随机分割 2/3 用于训练，1/3 用于测试

from sklearn.model_selection import train_test_split

from sklearn import metrics

X_train, X_test, y_train, y_test = train_test_split(data_X_v,data_y_v, test_size = 0.33, random_state = 4)

五数据分析

5.1探索性数据分析，提供可视化结果

通过热力图来观测每个特征列之间的关系

cm1 = data2.corr()

hm = sns.heatmap(cm1,cbar=True, annot=True, square=True, fmt='.2f')

plt.show()

从图中可以看出单位面积房价和距离公家车站远近，经纬度，便利店数相关性比较大。

5.2 描述性数据分析，提供可视化结果

使用describe进行查看数据

data_X.describe()

data_y.describe()

cols = ['Y 单位面积房价', 'X1 交易年月', 'X2 房龄',

'X3 最近公交站距离', 'X5 纬度', 'X6 经度']

zd = sns.pairplot(data_drop[cols], size=2.5)

plt.show()

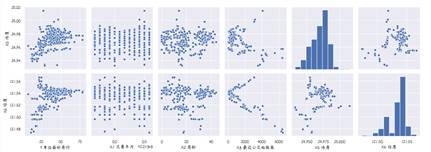
从上诉的一系列图中可以看出各个特征列之间的关系。

六回归预测分析

6.1介绍本次所用的四种预测模型

Linear Regression, Random Forest, XGBoost, Support Vector Machines上述四种模型时机器学习中常用的模型，具体的实现方法可以参考下文，本文会针对四种模型在这次的数据集上的表现做出对比。

6.2回归预测

6.2.0 本标题仅用于解释，下文中的四种模型全部包含回归预测、分析模型可靠性、误差分析、模型参数检验、报告回归结果

6.2.1 线性回归预测（Linear Regression）[2]

from sklearn.linear_model import LinearRegression

lm = LinearRegression()

lm.fit(X_train, y_train)

#print(lm.intercept_)

y_pred = lm.predict(X_train)

print('R^2:',metrics.r2_score(y_train, y_pred))

print('Adjusted R^2:',1 - (1-metrics.r2_score(y_train, y_pred))*(len(y_train)-1)/(len(y_train)-X_train.shape[1]-1))

print('MAE:',metrics.mean_absolute_error(y_train, y_pred))

print('MSE:',metrics.mean_squared_error(y_train, y_pred))

print('RMSE:',np.sqrt(metrics.mean_squared_error(y_train, y_pred)))

下面我来解释下打印的值的意思

𝑅^2 ：它是X和Y之间线性关系的度量。它被解释为因变量中可从自变量预测的方差的比例。

Adjusted 𝑅^2 ：调整后的 R-squared 比较包含不同数量预测变量的回归模型的解释力。

MAE ：它是误差绝对值的平均值。它测量两个连续变量之间的差异，这里是 y 的实际值和预测值。

MSE：均方误差 (MSE) 与 MAE 类似，但在对所有差值求和之前对差值进行平方，而不是使用绝对值。

RMSE：均方误差 (MSE) 与 MAE 类似，但在对所有差值求和之前对差值进行平方，而不是使用绝对值。

接下来可视化实际价格与预测值之间的差异（在训练集上预测）。

plt.scatter(y_train, y_pred)

plt.xlabel("Y 单位面积价格")

plt.ylabel("预测单位面积价格")

plt.title("真价格 vs 预测出的价格")

plt.show()

从图中可以看出线性回归模型在训练集上，预测和真实值基本一致。

接下来继续看残差和预测的关系（在训练集上预测）。

plt.scatter(y_pred,y_train-y_pred)

plt.title("预测 vs 残差")

plt.xlabel("预测")

plt.ylabel("残差")

plt.show()

可以看出残差大部分都是0上下，所以线性回归模型在训练集上的表现还是不错的。

接下来看残差直方图

sns.distplot(y_train-y_pred)

plt.title("残差直方图")

plt.xlabel("残差")

plt.ylabel("频率")

plt.show()

从图中可以看出残差符合正态分布，而且在0左右差不多对称。

刚才的一系列都是在训练集上测的，现在使用预测集进行测试。

y_test_pred = lm.predict(X_test)

acc_linreg = metrics.r2_score(y_test, y_test_pred)

print('R^2:', acc_linreg)

print('Adjusted R^2:',1 - (1-metrics.r2_score(y_test, y_test_pred))*(len(y_test)-1)/(len(y_test)-X_test.shape[1]-1))

print('MAE:',metrics.mean_absolute_error(y_test, y_test_pred))

print('MSE:',metrics.mean_squared_error(y_test, y_test_pred))

print('RMSE:',np.sqrt(metrics.mean_squared_error(y_test, y_test_pred)))

可以看出线性回归模型在测试集上的表现不如在训练集上的表现，但是总体来说，能预测出来大部分的结果。

6.2.2 使用随机森林预测[3]

from sklearn.ensemble import RandomForestRegressor

reg = RandomForestRegressor()

reg.fit(X_train, y_train)

y_pred = reg.predict(X_train)

print('R^2:',metrics.r2_score(y_train, y_pred))

print('Adjusted R^2:',1 - (1-metrics.r2_score(y_train, y_pred))*(len(y_train)-1)/(len(y_train)-X_train.shape[1]-1))

print('MAE:',metrics.mean_absolute_error(y_train, y_pred))

print('MSE:',metrics.mean_squared_error(y_train, y_pred))

print('RMSE:',np.sqrt(metrics.mean_squared_error(y_train, y_pred)))

在训练集上随机森林的表现和线性回归差不多

接下来可视化实际价格与预测值之间的差异（在训练集上预测）。

plt.scatter(y_train, y_pred)

plt.xlabel("Y 单位面积价格")

plt.ylabel("预测单位面积价格")

plt.title("真价格 vs 预测出的价格")

plt.show()

从图中可以看出随机森林和线性回归在训练集上差别不大，预测和真实值基本一致。

接下来继续看残差和预测的关系（在训练集上预测）。

plt.scatter(y_pred,y_train-y_pred)

plt.title("预测 vs 残差")

plt.xlabel("预测")

plt.ylabel("残差")

plt.show()

可以看出残差大部分都是0上下，所以随机森林模型在训练集上的表现还是不错的。

刚才的一系列都是在训练集上测的，现在使用预测集进行测试

y_test_pred = reg.predict(X_test)

acc_rf = metrics.r2_score(y_test, y_test_pred)

print('R^2:', acc_rf)

print('Adjusted R^2:',1 - (1-metrics.r2_score(y_test, y_test_pred))*(len(y_test)-1)/(len(y_test)-X_test.shape[1]-1))

print('MAE:',metrics.mean_absolute_error(y_test, y_test_pred))

print('MSE:',metrics.mean_squared_error(y_test, y_test_pred))

print('RMSE:',np.sqrt(metrics.mean_squared_error(y_test, y_test_pred)))

从这里可以看出随机森林在测试集上比线性回归模型好一些，但好的不多。

6.2.3 XGBoost模型（极端梯度增强模型）[4]

from xgboost import XGBRegressor

reg = XGBRegressor()

reg.fit(X_train, y_train)

y_pred = reg.predict(X_train)

print('R^2:',metrics.r2_score(y_train, y_pred))

print('Adjusted R^2:',1 - (1-metrics.r2_score(y_train, y_pred))*(len(y_train)-1)/(len(y_train)-X_train.shape[1]-1))

print('MAE:',metrics.mean_absolute_error(y_train, y_pred))

print('MSE:',metrics.mean_squared_error(y_train, y_pred))

print('RMSE:',np.sqrt(metrics.mean_squared_error(y_train, y_pred)))

这里可以看出XGBoost是比上述的两个模型都要优秀。

接下来看预测的真实度，这里代码不在重复粘贴了，代码和线性回归中的一样，横轴是真实值，纵轴是预测的值。（在测试集上）

可以看出两者基本完全一致，目前这个模型效果最好。

同样接下来看残差图，横轴是预测的值，纵轴是残差。

从残差这里可以看出，模型的预测存在不准的值，而且还不少。

刚才的一系列都是在训练集上测的，现在使用预测集进行测试。

y_test_pred = reg.predict(X_test)

acc_xgb = metrics.r2_score(y_test, y_test_pred)

print('R^2:', acc_xgb)

print('Adjusted R^2:',1 - (1-metrics.r2_score(y_test, y_test_pred))*(len(y_test)-1)/(len(y_test)-X_test.shape[1]-1))

print('MAE:',metrics.mean_absolute_error(y_test, y_test_pred))

print('MSE:',metrics.mean_squared_error(y_test, y_test_pred))

print('RMSE:',np.sqrt(metrics.mean_squared_error(y_test, y_test_pred)))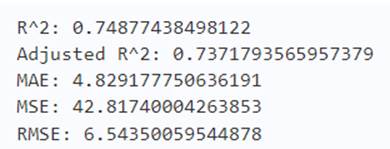

测试集上的表现就不行了，由此可见一味的拟合测试集不是好事。

6.2.4 支持向量机（SVM）[5]

from sklearn import svm

reg = svm.SVR()

reg.fit(X_train, y_train)

y_pred = reg.predict(X_train)

print('R^2:',metrics.r2_score(y_train, y_pred))

print('Adjusted R^2:',1 - (1-metrics.r2_score(y_train, y_pred))*(len(y_train)-1)/(len(y_train)-X_train.shape[1]-1))

print('MAE:',metrics.mean_absolute_error(y_train, y_pred))

print('MSE:',metrics.mean_squared_error(y_train, y_pred))

print('RMSE:',np.sqrt(metrics.mean_squared_error(y_train, y_pred)))

很显然，支持向量机不擅长这个工作。这样的话残差也不用看来一定效果不好。

不如直接看测试集上的效果。

y_test_pred = reg.predict(X_test)

acc_svm = metrics.r2_score(y_test, y_test_pred)

print('R^2:', acc_svm)

print('Adjusted R^2:',1 - (1-metrics.r2_score(y_test, y_test_pred))*(len(y_test)-1)/(len(y_test)-X_test.shape[1]-1))

print('MAE:',metrics.mean_absolute_error(y_test, y_test_pred))

print('MSE:',metrics.mean_squared_error(y_test, y_test_pred))

print('RMSE:',np.sqrt(metrics.mean_squared_error(y_test, y_test_pred)))

从上图可以看出在测试集上支持向量集，依然不行，应该是这四个模型里较差的一个了。

6.2.5 四个模型对比

对比四个模型在测试集上的表现

models = pd.DataFrame({

    'Model': ['Linear Regression', 'Random Forest', 'XGBoost', 'Support Vector Machines'],

    'R-squared Score': [acc_linreg*100, acc_rf*100, acc_xgb*100, acc_svm*100]})

models.sort_values(by='R-squared Score', ascending=False)