棒球数据分析

第1章 绪论

1.1 选题背景

美国职业棒球大联盟（MLB）一直以来都是全球最受关注的职业体育联赛之一。在现代体育竞技中，数据分析已经成为提升运动员表现和制定比赛策略的关键因素。MLB特别注重数据分析，其中击球出速度（Exit Velocity）和击球距离（Distance）是两个重要的指标。这些指标不仅可以衡量球员的击球力量，还能为教练和球探提供有价值的参考，帮助他们评估球员的潜力和表现。

尽管击球出速度和击球距离的数据已经被广泛收集和分析，但如何利用现有数据来预测未来的击球距离仍然是一个具有挑战性的问题。击球距离受到多种因素的影响，包括击球角度、击球甜蜜区（Sweet Spot）、硬击球率等。因此，通过构建一个有效的预测模型，可以帮助球队更好地理解和利用这些影响因素，从而优化训练计划和比赛策略。

本研究所使用的数据集涵盖了2015年至2022年间MLB球员的击球出速度数据，来源于知名的Baseball Savant网站。数据经过清洗和预处理，包含了多个相关特征，如球员的击球事件数（Batted Ball Events）、发射角度（Launch Angle）、甜蜜区百分比（Sweet Spot Percentage）、最大击球出速度（Max Exit Velocity）、平均击球出速度（Average Exit Velocity）等。

1.2 选题的意义和目的

本研究的主要目标是利用这些特征构建一个预测模型，准确预测球员的击球距离（Max Distance）。具体来说，我们希望通过机器学习技术，探索各个特征与击球距离之间的关系，并找出最具预测力的特征组合。

为了实现这一目标，我们将采用随机森林回归（Random Forest Regression）作为主要的预测模型。随机森林回归是一种集成学习方法，通过构建多个决策树并综合其结果来提高预测精度。我们将首先对数据进行标准化处理，以确保各特征在同一量级上进行比较。随后，我们将数据分割为训练集和测试集，训练模型并评估其性能。此外，我们还将尝试其他机器学习模型，如线性回归、梯度提升树和神经网络，以比较不同模型的效果。

通过本研究，我们期望能够构建一个高精度的击球距离预测模型，为MLB球队和球员提供实用的参考工具。这不仅有助于球员优化击球技术，也可以为教练在制定比赛策略时提供科学依据。最终，精准的预测和分析将有助于提升球队的整体竞争力。

数据分析在现代体育竞技中的作用日益重要，特别是在MLB这样的高水平联赛中。通过深入分析和预测击球出速度数据，我们可以更好地理解击球距离的影响因素，从而为球员和球队提供有价值的指导。这不仅体现了数据科学在体育领域的应用潜力，也为未来的研究提供了坚实的基础。

第2章 数据预处理

2.1 数据来源

本次数据来源于 Kaggle上的一个竞赛：最远击球距离预测。

图2.1 原始数据部分截图

图2.1中各列所表示的含义如下。
rank: 排名

year: 年份

player: 球员

batted_ball_events: 击球事件数

launch_angle: 发射角度

sweet_spot_percentage: 甜蜜区百分比（击球落在最佳击球角度范围内的次数占比）

max_ev: 最高击球出速度

average_ev: 平均击球出速度

fly_ball_line_drive_ev: 飞球和线驱球的击球出速度

ground_ball_ev: 滚地球的击球出速度

max_distance: 最远击球距离

average_distance: 平均击球距离

average_homerun: 平均本垒打距离

hard_hit_95mph+: 硬击球数（击球速度达到或超过95英里的次数）

hard_hit_percentage: 硬击球百分比（硬击球次数占比）

hard_hit_swing_percentage: 硬击球挥棒百分比（挥棒击出硬击球的比例）

total_barrels: 总强击球次数（强击球是一种衡量击球质量的指标，通常是指击球速度和发射角度都在一定范围内的击球）

barrels_batted_balls_percentage: 强击球占击球事件的百分比

barrels_plate_appearance_percentage: 强击球占打席数的百分比

2.2 数据导入以及预览

首先，导入了多个Python库，包括NumPy、Pandas、Matplotlib、Plotly和Seaborn，这些库用于数据处理、分析和可视化。接着，代码设置了Seaborn和Matplotlib的绘图样式，以确保图表具有一致的视觉效果，并初始化了Plotly的离线模式，使其能够在Jupyter Notebook中显示交互式图表。然后，代码遍历当前目录及其子目录中的所有文件并打印它们的路径，以检查文件结构。随后，代码加载了一个名为“data.csv”的MLB击球出速度数据集，并通过显示数据的前几行、数据集的形状、数据集的基本信息（包括列名、数据类型和非空值数量）以及生成统计摘要（使用红色渐变背景增强可视化效果）来进行初步的数据检查。

图2.2 数据集的信息

这些步骤可以快速了解数据集的基本结构和特征，为后续的深入分析和建模做好准备。具体代码如下:

1. import numpy as np 
2. import pandas as pd 
3. import matplotlib.pyplot as plt 
4. import plotly.express as px 
5. import seaborn as sns 
7. sns.set(rc = {"figure.figsize":(14, 6)}) 
8. plt.style.use("fivethirtyeight")
10. from plotly.offline import plot, iplot, init_notebook_mode
11. import plotly.graph_objs as go
12. init_notebook_mode(connected=True)
14. import os
15. for dirname, _, filenames in os.walk('./'):
16.     for filename in filenames:
17.         print(os.path.join(dirname, filename))
19. df = pd.read_csv("./mlb-batter-exit-velocity.csv", encoding='unicode_escape')
21. df.head()
22. df.shape
23. df.info()
24. df.describe().style.background_gradient(cmap = "Reds")

第3章 数据预处理及各列可视化分析

3.1 发射角度可视化

使用Plotly库创建并展示一个带有箱线图边际的发射角度直方图，以便可视化并分析MLB数据集中击球发射角度的分布情况。首先，代码通过指定数据源和列名，设置直方图的边际类型为箱线图，并为发射角度添加标签和标题。颜色设置为一个特定的颜色序列（#FF6464）。然后，代码调整了直方图的柱间距，并应用了“plotly_dark”模板，使背景变暗，并设置了字体样式和颜色，以提高图表的可读性和视觉效果。最后，调用fig.show()显示生成的交互式图表。整体目的是提供一个清晰、易于解释的可视化图表，帮助我们理解发射角度数据的分布特征。

图3.1 平均击球角度

具体的代码如下：

1. fig = px.histogram(df, x = "launch_angle", marginal = "box",
2.                    labels = {"launch_angle": "Average Launch Angle"},
3.                    title = "Histogram of Average Launch Angle ", 
4.                    color_discrete_sequence = ["#FF6464"])
5. fig.update_layout(bargap = 0.2)
6. fig.update_layout(template = "plotly_dark", font = dict(family = "PT Sans", size = 18, color = "#FFFFFF"))
7. fig.show()

3.2 平均击球速度

创建并展示一个带有箱线图边际的击球平均出速度（Average Exit Velocity）直方图，以便可视化和分析MLB数据集中击球出速度的分布情况。首先，代码使用Plotly Express库创建了一个直方图，将数据集中的“average_ev”列作为X轴数据，并在图表的边缘添加一个箱线图，以提供额外的统计信息，如中位数和四分位数。直方图的颜色设置为一个特定的颜色序列（#FFAF64），使其具有一致的视觉风格。接着，代码为X轴添加了标签“Average Exit Velocity”，并为图表添加了标题“Histogram of Average Exit Velocity (MPH) ��”。随后，代码通过调整柱间距（bargap）来优化图表的可读性，并应用了“plotly_dark”模板，使背景变暗，从而突出图表内容。字体样式和颜色也进行了设置，使用了“PT Sans”字体，字体颜色为白色，大小为18，以提高整体视觉效果和可读性。最后，代码调用fig.show()显示生成的交互式图表。总体而言，这段代码旨在提供一个清晰且信息丰富的可视化工具，帮助我们更好地理解击球平均出速度的数据分布及其统计特征。

图3.2 平均击球速度

具体代码如下:

1. fig = px.histogram(df, x = "average_ev", marginal = "box",
2.                    labels = {"average_ev": "Average Exit Velocity"},
3.                    title = "Histogram of Average Exit Velocity (MPH) ��",
4.                    color_discrete_sequence = ["#FFAF64"])
5. fig.update_layout(bargap = 0.2)
6. fig.update_layout(template = "plotly_dark", font = dict(family = "PT Sans", size = 18, color = "#FFFFFF"))
7. fig.show()

3.3 最大击球速度

创建并展示一个带有箱线图边际的最大击球出速度（Max Exit Velocity）直方图，以便可视化和分析MLB数据集中最大击球出速度的分布情况。首先，代码使用Plotly Express库创建了一个直方图，将数据集中的“max_ev”列作为X轴数据，并在图表的边缘添加一个箱线图，以提供额外的统计信息，如中位数和四分位数。直方图的颜色设置为一个特定的颜色序列（#FF64FF），以确保图表具有一致的视觉效果。接着，代码为X轴添加了标签“Max Exit Velocity”，并为图表添加了标题“Histogram of Max Exit Velocity (MPH) ��”。随后，代码通过调整柱间距（bargap）来优化图表的可读性，并应用了“plotly_dark”模板，使背景变暗，从而突出图表内容。字体样式和颜色也进行了设置，使用了“PT Sans”字体，字体颜色为白色，大小为18，以提高整体视觉效果和可读性。最后，代码调用fig.show()显示生成的交互式图表。总体而言，这段代码旨在为提供一个清晰且信息丰富的可视化工具，帮助我们更好地理解最大击球出速度的数据分布及其统计特征。

图3.3 最大击球速度

具体代码如下：

1. fig = px.histogram(df, x = "max_ev", marginal = "box",
2.                    labels = {"max_ev": "Max Exit Velocity"},
3.                    title = "Histogram of Max Exit Velocity (MPH) ��",
4.                    color_discrete_sequence = ["#FF64FF"])
5. fig.update_layout(bargap = 0.2)
6. fig.update_layout(template = "plotly_dark", font = dict(family = "PT Sans", size = 18, color = "#FFFFFF"))
7. fig.show()

3.4 各个特征相关性分析

进行特征之间的相关性分析，并使用热力图可视化展示相关性矩阵。首先，代码通过select_dtypes方法从DataFrame中选择数值类型的列，生成一个包含数值型数据的子数据集numeric_df。接着，使用corr方法计算numeric_df中各列之间的相关系数，得到一个相关性矩阵correlation_matrix。然后，代码创建一个大小为10x10的新图形（figure），并使用Seaborn库的heatmap函数绘制热力图。在热力图中，相关性矩阵中的每个值都用颜色表示，颜色的深浅程度表示相关性的强度，同时在每个方块中显示相关系数的数值，并通过参数annot=True实现。另外，通过设置cbar=False隐藏颜色条，cmap='Spectral'指定颜色映射为'Spectral'，fmt='.1f'指定显示的数字格式为一位小数。整体而言，这段代码的目的是通过热力图直观地展示特征之间的相关性，以帮助我们理解数据集中各个特征之间的关系。

图3.4 各列相关性分析

具体代码如下:

1. numeric_df = df.select_dtypes(include=[np.number])
2. correlation_matrix = numeric_df.corr()
4. plt.figure(figsize = (10,10))
5. sns.heatmap(correlation_matrix, annot=True, cbar=False, cmap='Spectral', fmt='.1f')

3.5 发射角度和平均初速度的关系

遍历2015年到2022年的每一年数据，并根据每年的数据绘制一个极坐标散点图。首先，在每次循环中，代码根据当前循环的年份从数据框df中筛选出对应年份的数据，并存储在名为df0的新数据框中。接着，代码使用Plotly Express库的scatter_polar函数创建一个极坐标散点图。在散点图中，角度（theta）和径向距离（r）分别表示发射角度（launch_angle）和平均出速度（average_ev），颜色（color）表示平均出速度。散点图的参数设置包括了角度范围（range_theta）、起始角度（start_angle）、透明度（opacity）、标签（labels）、颜色范围（range_color）、颜色连续色阶（color_continuous_scale）以及旋转方向（direction）。随后，代码更新了图形的布局，使用了暗色背景模板（"plotly_dark"），并设置了字体样式和颜色，以提高图表的可读性。最后，代码更新了图表的标题，将当前循环的年份嵌入到标题中，并调用fig.show()显示生成的极坐标散点图。整体而言，这段代码的目的是通过循环遍历每年的数据，绘制多个极坐标散点图，以便比较不同年份间平均发射角度和平均出速度的关系，并观察可能存在的趋势和变化。

图3.5 15年平均击球角度和速度

图3.6 16年平均击球角度和速度

图3.7 17年平均击球角度和速度

具体代码如下:

1. for year in range(2015, 2023):
2.     
3.     df0 = df[df["year"] == year]
4.     
5.     fig = px.scatter_polar(df0, r="launch_angle", theta= "launch_angle", color = "average_ev",
6.                            range_theta=[0,30],
7.                            start_angle=0, opacity = 0.8,
8.                            labels = {"average_ev": "EV"},
9.                            range_color = (83, 90),
10.                            color_continuous_scale = "Turbo",
11.                            direction="counterclockwise")
12.     fig.update_layout(template = "plotly_dark", font = dict(family = "PT Sans", size = 14, color = "#FFFFFF"))
13.     fig.update_layout(title = f"Average Launch Angle and Average Exit Velocity in {year} ⚾")
14.     fig.show()

3.6 击球事件中的桶击球百分比

创建一个散点图，用于展示数据集中排名前50名球员的每年击球事件中的桶击球百分比。首先，代码从数据框df中筛选出排名在前50名以内的球员数据，并将筛选结果存储在名为df0的新数据框中。接着，使用Plotly Express库的scatter函数创建一个散点图，其中x轴表示球员的排名（rank），y轴表示年份（year），颜色表示桶击球百分比（barrels_batted_balls_percentage）。散点图的参数设置包括了hover_data（悬停数据，即鼠标悬停在数据点上时显示的附加信息，这里显示球员姓名）、颜色连续色阶（color_continuous_scale）以及标签（labels）和标题（title）。接着，代码使用update_traces方法更新散点的样式，将散点大小设置为8，形状设置为方形，以改善图表的可读性。最后，代码更新了图形的布局，使用了暗色背景模板（"plotly_dark"），并设置了字体样式和颜色，以提高图表的可读性。最终，调用fig.show()显示生成的散点图。整体而言，这段代码的目的是通过散点图直观地展示排名前50名球员每年击球事件中的桶击球百分比，以便观察该指标随时间和排名的变化情况，并可能进行球员之间的比较。

图3.8 每年击球事件中的桶击球百分比散点图

1. df0 = df[df["rank"] <= 50]
2. fig = px.scatter(df0, x = "rank", y = "year", hover_data = ["player"],
3.                  color = "barrels_batted_balls_percentage", color_continuous_scale = "Turbo",
4.                  labels = {"barrels_batted_balls_percentage": "Barrel %"},
5.                  title = "Barrel Percentage of Batted Ball Events by Year and Rank")
7. fig.update_traces(marker = dict(size = 8, symbol = "square")) # scaling the markers
8. fig.update_layout(template = "plotly_dark", font = dict(family = "PT Sans", size = 18, color = "#FFFFFF"))
9. fig.show()

3.6 最远击球距离和其他列的关系

首先画散点图，分析最远击球距离和平均距离的关系。

图3.9 最远击球距离和平均距离散点图

barrels_plate_appearance_percentage和最远击球距离的关系。

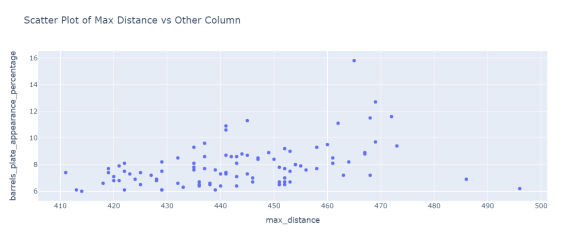
图3.10 最远击球距离和barrels_plate_appearance_percentage散点图

不同年份和最远击球距离的关系。

图3.11 最远击球距离和年份散点图

可以看出每一年的区别都不大。

第4章 建模分析

4.1 特征工程

我们已完成对数据的可视化分析，接下来进行特征提取。首先，我们删除了包含空值的行，以确保数据的完整性。然后，我们删除了名为 'player' 的列，因为在预测最大距离时，球员的名字并不是一个重要的特征。接下来，我们将数据的类型转换为数值型，这是因为机器学习模型通常只能处理数值型数据。然后，我们确定了特征列和目标列，特征列包括除了最大距离以外的所有列，而目标列则是最大距离。最后，我们使用 train_test_split 函数将数据集划分为训练集和测试集，其中测试集占总数据的 20%，而训练集则用于训练模型。具体代码如下：

1. # 删除包含空值的行
2. df.dropna(inplace=True)
4. # 删除 'player' 列
5. df.drop(columns=['player'], inplace=True)
7. # 转换数据类型为数值型
8. df = df.apply(pd.to_numeric)
10. # 确定特征和目标列
11. X = df.drop(columns=['max_distance'])
12. y = df['max_distance']
14. # 划分训练集和测试集
15. X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

4.2 模型构建训练和预测

多元线性回归是一种统计模型，用于分析多个自变量与一个因变量之间的线性关系。通过拟合一个包含多个自变量的线性模型，它可以预测因变量的数值。这种方法假设因变量与多个自变量之间存在线性关系，其目标是找到最佳的回归系数，以最小化预测值与实际观测值之间的误差。通常，多元线性回归使用最小二乘法来估计回归系数，通过最小化残差平方和来求解。这种方法能够得到回归系数的解析解，从而使得计算简单高效。在实际应用中，多元线性回归常用于解释因变量受多个自变量影响的情况，例如在经济学、金融学和社会科学等领域。它为研究人员提供了一种有效的分析工具，可以预测因变量在多个自变量影响下的变化趋势，为决策提供重要参考。随机森林算法是一种集成学习方法，通过构建多个决策树并取其结果的平均值来进行预测。它的原理基于决策树的思想，但在构建每棵树时引入了随机性。具体而言，随机森林会从训练集中随机选择样本和特征进行训练，使得每棵树都是不同的。在预测时，随机森林通过投票或取平均值的方式，综合多棵树的结果来获得最终预测结果。这种随机性和集成的方法使得随机森林具有较强的泛化能力和抗过拟合能力，适用于各种分类和回归问题。同时，由于每棵树的构建过程是独立的，随机森林的训练和预测速度也相对较快，适用于大规模数据集和实时应用场景。

这里我们选用不同的模型来预测数据，并且将画成了两张图，一张是散点图一张是折线图，从图中可以看出线性回归的效果并不好，随机森林的效果好。通过学习我们发现，随机森林通常比线性回归更好，特别是在处理复杂和非线性关系的数据时。这是因为随机森林是一种集成学习方法，通过构建多个决策树来提高预测性能和稳定性。每个决策树在训练时只使用数据的一个子集和特征的一个子集，从而减少过拟合的风险。随机森林能够捕捉数据中的非线性关系和复杂的交互作用，而线性回归假设变量之间存在线性关系，因此在面对非线性数据时性能有限。此外，随机森林具有较强的抗噪能力和鲁棒性，能够处理缺失值和异常值，提供更准确和可靠的预测结果。

图4.1 预测结果散点图

图4.2 预测结果折线图

具体代码如下：

1. import pandas as pd
2. from sklearn.model_selection import train_test_split
3. from sklearn.linear_model import LinearRegression
4. from sklearn.ensemble import RandomForestRegressor
5. import matplotlib.pyplot as plt
6. import seaborn as sns
7. from sklearn.model_selection import cross_val_predict
11. # 转换数据类型为数值型
12. df = df.apply(pd.to_numeric)
14. # 确定特征和目标列
15. X = df.drop(columns=['max_distance'])
16. y = df['max_distance']
18. # 划分训练集和测试集
19. X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
21. # 创建线性回归模型
22. lr_model = LinearRegression()
23. # 使用五折交叉验证进行预测
24. lr_pred = cross_val_predict(lr_model, X, y, cv=2)
26. # 创建随机森林模型
27. rf_model = RandomForestRegressor()
28. # 使用五折交叉验证进行预测
29. rf_pred = cross_val_predict(rf_model, X, y, cv=2)
31. # 可视化预测结果
32. plt.figure(figsize=(10, 6))
34. # 绘制线性回归模型的预测结果
35. plt.scatter(y, lr_pred, color='blue', label='Linear Regression')
36. # 绘制随机森林模型的预测结果
37. plt.scatter(y, rf_pred, color='red', label='Random Forest')
39. # 添加标签和图例
40. plt.xlabel('True Values')
41. plt.ylabel('Predictions')
42. plt.title('Predictions vs True Values')
43. plt.legend()
45. # 绘制一条完美预测的对角线
46. plt.plot([y.min(), y.max()], [y.min(), y.max()], color='black', linestyle='--')
48. plt.show()
50. # 创建线性回归模型
51. lr_model = LinearRegression()
52. # 使用五折交叉验证进行预测
53. lr_pred = cross_val_predict(lr_model, X, y, cv=2)
55. # 创建随机森林模型
56. rf_model = RandomForestRegressor()
57. # 使用五折交叉验证进行预测
58. rf_pred = cross_val_predict(rf_model, X, y, cv=2)
60. # 绘制前 100 个真实值和预测值的折线图
61. plt.figure(figsize=(10, 6))
63. # 绘制线性回归模型的前 100 个预测结果
64. plt.plot(range(100), y_test[:100], label='True Values', marker='o')
65. plt.plot(range(100), lr_pred[:100], label='Linear Regression Predictions', marker='x')
66. plt.plot(range(100), rf_pred[:100], label='rf Regression Predictions', marker='o')
67. # 添加标签和图例
68. plt.title('True Values vs Predictions (Linear Regression)')
69. plt.xlabel('Index')
70. plt.ylabel('Max Distance')
71. plt.legend()
72. plt.grid(True)
74. plt.show()

1. 总结

本次实验旨在探讨如何利用历史棒球数据来预测击球的最远距离。具体而言，我们将击球数据视为一个回归任务，并尝试使用机器学习算法进行预测。在本次实验中，我们选择了随机森林和线性回归两种模型进行建模和预测。

首先，我们收集了历史棒球数据，包括击球事件数量、发射角度、甜蜜点百分比、最大击球速度、平均击球速度等。然后，我们将数据划分为训练集和测试集，并对数据进行预处理，包括删除缺失值、特征提取等步骤。接着，我们选择了随机森林和线性回归两种模型进行建模，并使用训练集对模型进行训练。训练完成后，我们利用测试集对模型进行评估，并比较不同模型的预测效果。

通过实验结果的分析，我们发现随机森林模型在预测击球最远距离方面表现较好，其预测结果与实际距离较为接近。而线性回归模型的预测效果相对较差，可能是由于模型过于简单，无法捕捉到击球数据的复杂关系。此外，我们还提到，虽然其他方法如神经网络可能在处理复杂数据上具有优势，但在本次实验中未加以实现。

综上所述，本次实验通过机器学习方法尝试了对棒球击球最远距离的预测，并进行了模型比较和评估。实验结果表明随机森林模型在这一任务中表现较佳，为未来的预测提供了一种有效的方法。然而，对于不同的数据集和问题，选择合适的模型和方法仍然需要进一步的研究和探讨。