高中物竞-第一章-运动学的基本概念（完整版）

1.参考系和坐标系

自然界的一切物体都处于永恒的运动中。要描述一个物体的运动，首先必须选定某个其他物体做参考，这种用来做参考的物体称为参考系。描述一个物体的运动，参考系可以任意选择。但是，选择不同的参考系对同一运动的描述一般说来是不同的。
应当注意的是，合理选择参考系，会使运动的研究变得简便。例如，我们研究地面上的物体运动时，通常选地面为参考系；研究卫星的运动时，通常选地心为参考系；研究地球的公转时，通常选太阳为参考系。
为了定量描述质点的位置及其变化规律，我们可以在参考系上建立一个适当的坐标系。这样，质点的位置就可以用位置坐标来表示了。

2.位矢和位移

（1）位矢

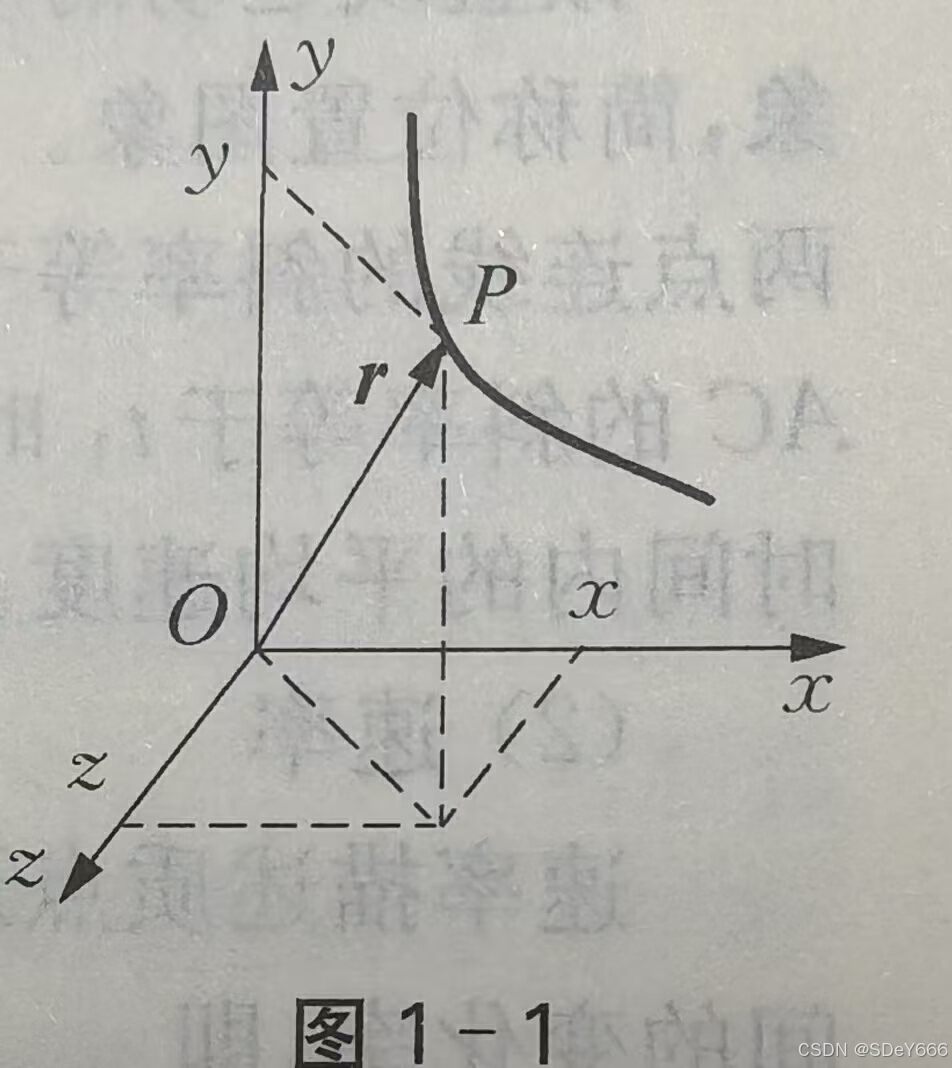
质点在某时刻的位置是质点在该时刻的空间所在。为了使位置的描述和位移的计算一致，引入位置矢量（简称位矢）。位矢定义为自坐标原点到质点位置的空间矢量。如图1-1所示，设某时刻质点位于 P 点，其坐标为$（x.y,z)$，则位矢$$r=xi+yi+zk,$$
其中$i、j、k$是$x、y、z$轴的单位矢量。
质点运动时，位矢随时间变化。位矢末端（质点位置）坐标随时间变化的方程称为运动方程。在直角坐标系中，运动方程可写为三个分量方程$$x=x(t),$$$$y=y(t),$$$$z=z(t)。$$
质点运动时，位矢末端在空间描绘的曲线，称为质点的运动轨迹，质点运动轨迹的曲线方程称为轨迹方程。在直角坐标系中，轨迹方程为$$f(x,y,z)=0。$$

（2）位移

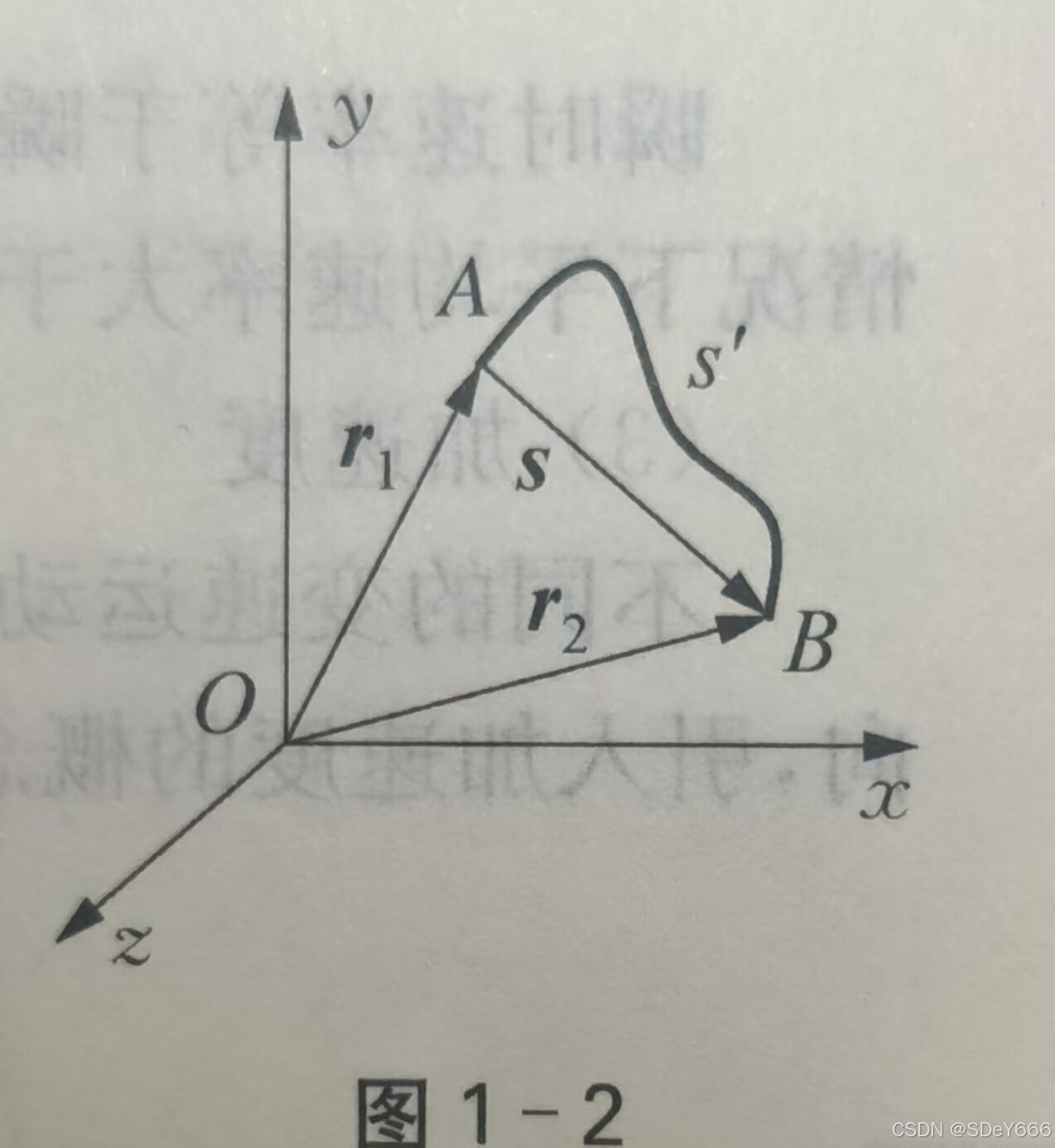如图1-2所示，设质点在△ t 的时间内沿曲线从 A 点运动到 B 点，位矢由r1变为r2，则位矢的变化 Ar =r2- r ，反映了质点位置的变化，称为位移，即$$s=△r=r_2-r_1。$$位移的大小也叫运动的距离。

（3）路程

质点通过的路径的长度叫做路程。
路程与位移是两个不同的物理量。路程是标量，位移是矢量，而且路程与位移的大小通常不相等。只有质点做单向直线运动，路程才等于位移的大小。但是，如果质点运动的时间极短$（△t\to 0)$，则可以认为路程等于位移的大小。

3.速度和加速度

（1）速度

不同的运动，质点位置变化的快慢和方向一般不同。为了描述质点位置变化的快慢和方向，引入速度的概念。质点在某时刻的速度称为瞬时速度，简称速度，定义为位矢对时间的变化率，即$$v=\frac{dr}{dt},$$
速度的方向轨沿迹的切线方向。
质点在一段时间$t$内的移位与所用时间的比值称为这段时间内的平均速度，即$$v=\frac{s}{t},$$
其方向与位移的方向相同。平均速度只能粗略地描述质点在一段时间内位置变化的平均快慢与方向。

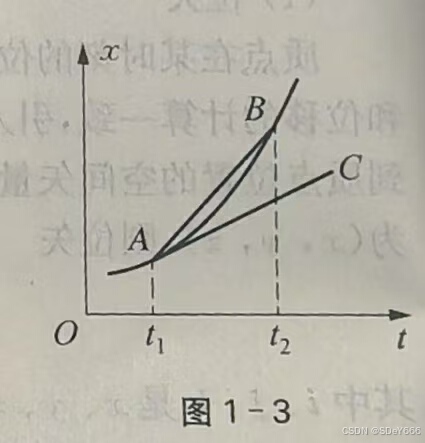
做直线运动的质点,位置坐标随时间的关系图象称为位置一时间图4工方向。象,简称位置图象。位置图线上某点切线的斜率等于该时刻的瞬时速度两点连线的斜率等于这段时间内的平均速度。如图1-3所示,$A$点切线$AC$的斜率等于$t$时刻的瞬时速度,$A、B$两点连线$AB$的斜率等于$t_1-t_2$时间内的平均速度。

（2）速率

速率描述质点运动的快慢。瞬时速率(简称为速率)定义为路程对时间的变化率,即$$v‘=\frac{ds‘}{dr}。$$
平均速率定义为路程与所用时间的比值$$v‘=\frac{s‘}{t}。$$
瞬时速率等于瞬时速度的大小。质点做单向直线运动时平均速率等于平均速度的大小,其他情况下平均速率大于平均速度的大小。

(3)加速度

不同的变速运动,质点速度变化的快慢和方向一般不同。为了描述质点速度变化的快慢和方向,引人加速度的概念。加速度定义为速度对时间的变化率,即$$a=\frac{dv}{dt}。$$做直线运动的质点,速度随时间的关系图象称为速度一时间图象,简称速度图象。速度图线上某点切线的斜率等于该时刻的瞬时加速度,两点连线的斜率等于这段时间内的平均加速度。速度一时间图线下的“面积”等于这段时间内的位移。应当注意的是,当图线在横轴上方时，“面积”取正值,表示位移的方向与规定的正方向相同;当图线在横轴下方时,“面积”取负值,表示位移的方向与规定的正方向相反。

本课节已结束，感谢您的观看，下节更精彩

作者留言：本系列为 高中物竞，全系列限免至2026.01.01 - SDeY666