给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:s = "abc" 输出:3 解释:三个回文子串: "a", "b", "c"
示例 2:
输入:s = "aaa" 输出:6 解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
提示:
1 <= s.length <= 1000s由小写英文字母组成
思路:
动规五部曲:
1.确定dp数组(dp table)以及下标的含义
dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话,我们会发现很难找到递归关系。
dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
注意 j >= i
2.确定递推公式
当s[i]与s[j]不相等
dp[i][j]一定是false。
当s[i]与s[j]相等时
情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
情况二:下标i 与 j相差为1,例如aa,也是回文子串
情况三:下标:i 与 j相差大于1的时候
这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
if(s.charAt(i)!=s.charAt(j)){dp[i][j]=false; }
if(s.charAt(i)==s.charAt(j)){
if(j-i<=1){
//情况1,2
dp[i][j]=true;
result++;
}else{
//情况3
if(dp[i+1][j-1]){
dp[i][j]=true;
result++;
}
}
}
3.dp数组如何初始化
dp[i][j]初始化为false
4.确定遍历顺序
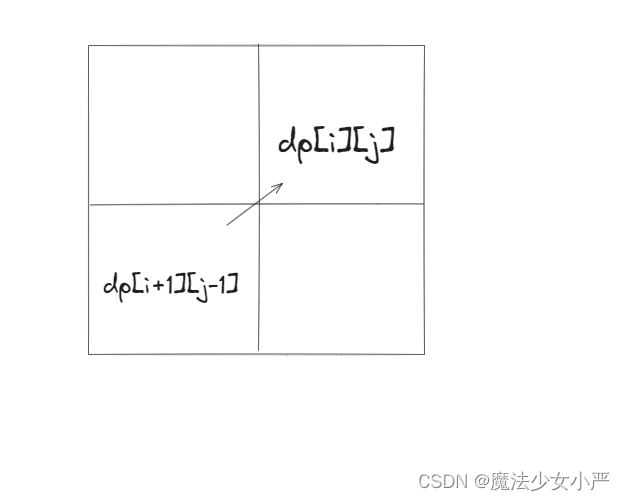
首先从递推公式中可以看出,情况三是根据dp[i + 1][j - 1]是否为true,在对dp[i][j]进行赋值true的
dp[i + 1][j - 1] 在 dp[i][j]的左下角
所以一定要从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的
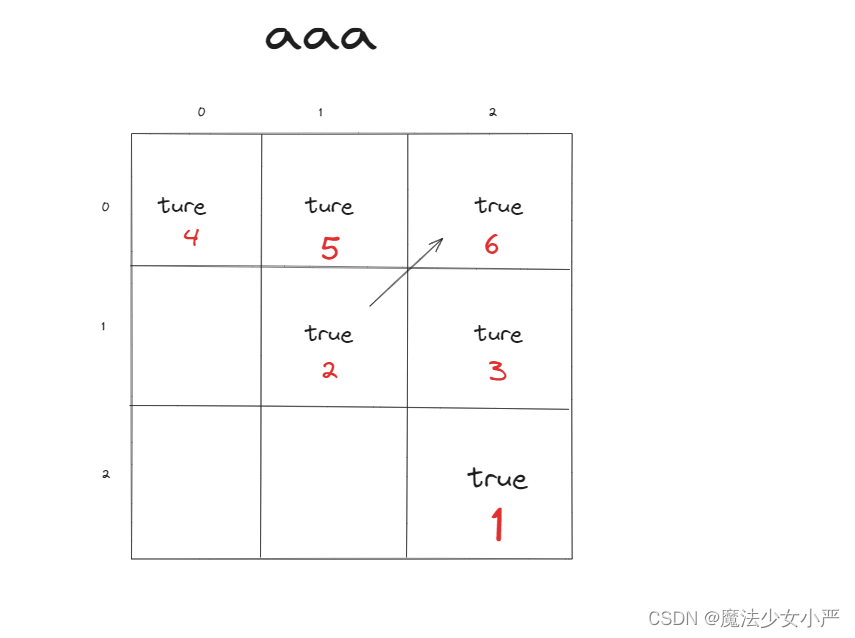
5.举例推导dp数组
代码参考:
class Solution {
public int countSubstrings(String s) {
boolean[][] dp=new boolean[s.length()][s.length()];
int result=0;
for(int i=s.length()-1;i>=0;i--){
for(int j=i;j<s.length();j++){
if(s.charAt(i)!=s.charAt(j)){
dp[i][j]=false;
}else{
if(j-i<=1){
dp[i][j]=true;
result++;
}else{
if(dp[i+1][j-1]){
dp[i][j]=true;
result++;
}
}
}
}
}
return result;
}
}给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
示例 1:
输入:s = "bbbab" 输出:4 解释:一个可能的最长回文子序列为 "bbbb" 。
示例 2:
输入:s = "cbbd" 输出:2 解释:一个可能的最长回文子序列为 "bb" 。
提示:
1 <= s.length <= 1000s仅由小写英文字母组成
思路:
本题是求回文子序列,而不是回文子串,回文子串是要连续的,回文子序列可以不是连续的!
动规五部曲分析如下:
1确定dp数组(dp table)以及下标的含义
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
2.确定递推公式
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}3.dp数组如何初始化
需要手动初始化一下,当i与j相同,那么dp[i][j]一定是等于1的,即:一个字符的回文子序列长度就是1。其他情况dp[i][j]初始为0
4.确定遍历顺序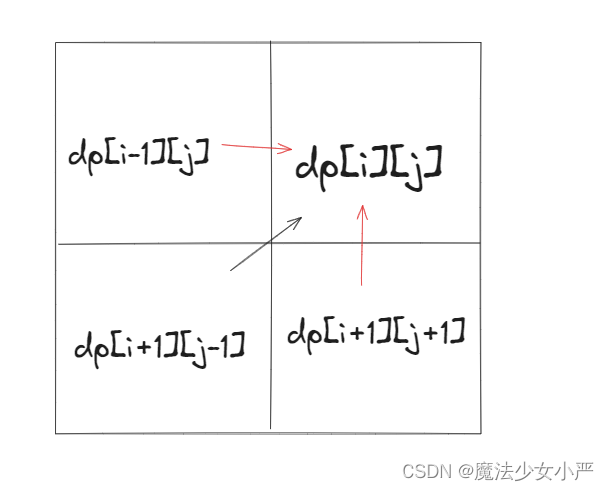
遍历i的时候一定要从下到上遍历,这样才能保证下一行的数据是经过计算的。
j的话,可以正常从左向右遍历。
5.举例推导dp数组
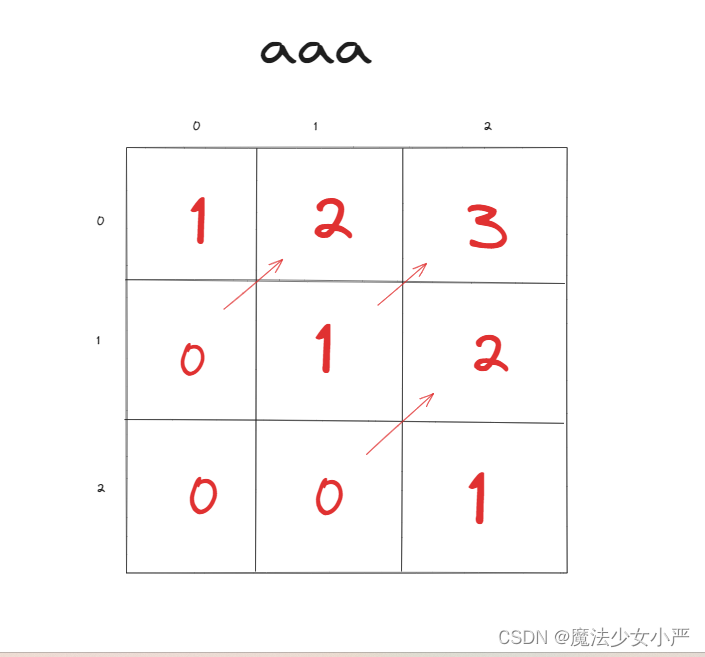
代码参考:
class Solution {
public int longestPalindromeSubseq(String s) {
int [][] dp=new int[s.length()][s.length()];
//初始化
for(int i=0;i<s.length();i++){
dp[i][i]=1;
}
for( int i=s.length()-2;i>=0;i--){
for(int j=i+1;j<s.length();j++){
if(s.charAt(i)==s.charAt(j)){
dp[i][j]=dp[i+1][j-1]+2;
}else{
dp[i][j]=Math.max(dp[i][j-1],dp[i+1][j]);
}
}
}
return dp[0][s.length()-1];
}
}




















 1235
1235











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








