算法学习过程——欧拉（费马小定理、欧拉函数、欧拉定理、欧拉降幂、欧拉筛法）_1

引言

        正文开始之前先说一说废话，在学习数论系列的算法有一种勿入高端局的感觉，其实也正常，毕竟一些定理从名字上拗口，如果见识多了了解多了，再说出一些以洋人名字命名的定理公式总会让人觉得很牛逼，其实学习的内容并不难，只要思路跟着走。

正文

        标题标注的即为讲解顺序，后面内容的讲解需要前面内容的基础，内容较多，分为两篇讲解，本篇主要讲解费马小定理、欧拉函数、欧拉定理。

费马小定理

        

定义

        看似乎不难，那再详细讲解一下：

        p 为素数（质数），且 a 与 p 互素（即 gcd（a，p）= 1 ），则有

• 注： 是在对 p 取模的情况下恒等于 1

证明：

        设 p 是一个 质数，且 a 是不为 p 的倍数的数。

设一个序列 A = { 1, 2, 3, ... , p-1 }，则有  ( p 是质数 ) ，

因为 a 不是 p 的倍数，所以无论 1 ~ p - 1 之间谁乘 a 都是独一无二，即 每一个  独一无二

且都不是 p 的倍数，所以 在 mod p 的情况下 每一个  也独一无二（难理解的在这一点）

可以理解为从 0 开始每次都加 a 直到恰好小于 p ，再多一个 a 就大于 p 时，再加一个 a

再 mod p 会使得结果不为 0 ，再回到第一步每次都加 a ，因为初始值不再为 0 所以每次加 a 都和

mod p 之前每次加 a 的数都不一样，如此可证的在 mod p 的情况下 每一个  也独一无二

设  则 

            

至此证明完成，还有其他证明方法，在此不再说明。

欧拉函数

定义

        定义比较简单，但是可能不知道怎么求？确实让人头大，要一个一个判断前面没一个数是否和 n 互质吗？

证明

        这个编辑器好难用，还是直接放图片了

代码实现

        设   ，p 为质数，则 

根据唯一分解定理（不了解的可以先看我之前发的数论基础的素数部分（tip：素数与质数是一样的，只是叫法不同）算法学习过程——数论基础）可得

设 （符号表示连乘）  ，可以用 for 循环实现连乘

#include <cmath>

int phi(int n)//求欧拉函数的值
{
	int res = n;
	int m = sqrt(x);
	for(int i = 2;i <= m;++i)//相当于质因数分解
	{
		if(x % i)continue;
		res = res / i *(i-1);
		while(x % i == 0)x /= i;//由于每个数都只乘一次，所以把多余部分去掉
	}
	if(n > 1)res = res / n * (n-1);//如果最后不为1，则表示最后一个数也是质因数
	return res;
}

也可以改写成以下形式，会提升一点点效率

#include <cmath>

int phi(int n)//求欧拉函数的值
{
	int res = n;
	for(int i = 2;i <= n / i;++i)//相当于质因数分解 防止i*i超出限制
	{
		if(x % i)continue;
		res = res / i *(i-1);
		while(x % i == 0)x /= i;//由于每个数都只乘一次，所以把多余部分去掉
	}
	if(n > 1)res = res / n * (n-1);//如果最后不为1，则表示最后一个数也是质因数
	return res;
}

欧拉定理

        定义较为简单，只有一个公式

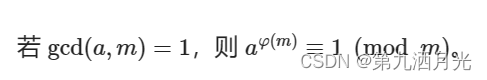
当 m 是质数的时候有 ,与费马最小定理一致。

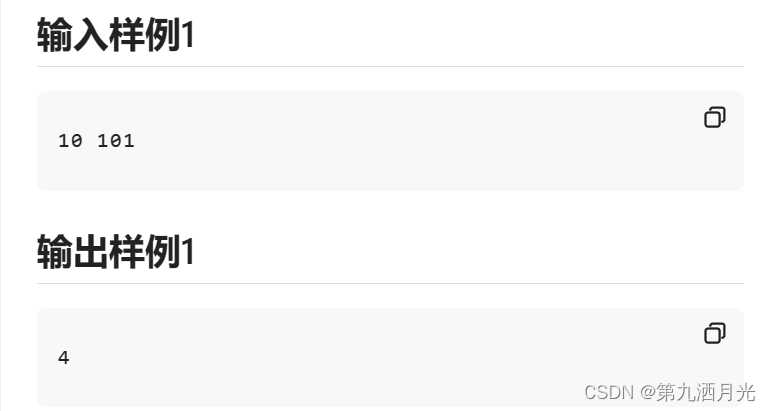
实践练习

        

思路：按照所学，似乎 n - 1 就是可以满足答案的数，可是让我们寻找最小，在满足题目等式成立的情况下可以去 n - 1 的因数中寻找答案。

#include "bits/stdc++.h"
using namespace std;
const int MOD = 998244353;
const int p = 1e6+7;
const int N = 209;
#define int long long
int a, n;

int qmi(int a,int b,int p)//快速幂
{
	int res = 1;
	while(b)
	{
		if(b & 1)res = res * a % p;
		a = a * a % p;
		b >>= 1;
	}
	return res;
}
int phi(int x)//求欧拉函数的值
{
	int res = x;
	int m = sqrt(x);
	for(int i = 2;i <= m;++i)
	{
		if(x % i)continue;
		res = res / i *(i-1);
		while(x % i == 0)x /= i;
	}
	if(x > 1)res = res / x * (x-1);
	return res;
}
void solve(){
	cin >> a >> n;
	int ph = phi(n);
	int ans = ph;
	int m = sqrt(n);
	for(int i = 1;i <= m;++ i)
	{
		if(ph % i)continue;
		
		if(qmi(a,i,n) == 1)ans = min(ans,i);
		if(i != ph / i)//两个因数不一样
		{
			if(qmi(a,ph / i,n) == 1)ans = min(ans,ph / i);
		}
	}
	cout << ans << '\n';
}
signed main() {
	ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(0);
	int _ = 1;
	//cin >> _;
	while(_--)solve();
	return 0;
}

这类模板题只要样例调试对了一般不会出错，大家放心。

总结

        初步数论中欧拉函数、欧拉定理，自用复习以及分享给大家，有任何问题可以留言或私信。