学习了一天matlab,把自己从书上学到的知识写出来。
重要的概念
常微分方程 (ordinary differential equation,简称ODE)是未知函数中只含有一个自变量的微分方程。
偏微分方程(partial differential equation,简称PDE)是未知函数是多元函数的微分方程。
CAE求解方法一般有两种
显式(Explicit)第n步结果可以从n-1, n-2, ......1步的结果直接推导出来,迭代时每步的计算量很小,但迭代增量也有限制,不能太大,否则会出现发散。
隐式(Implicit)第n步的计算结果不能直接从前面的结果推导出来,必须做进一步的求解,这样,迭代时每步的计算量很大。
泰勒公式
若 f(x) 在 x = 0 点直到 n + 1 阶连续导数,则
称为 f(x) 在 x = 0 点关于 x 的幂函数展开式,又称为 Taylor 公式,式中Rn(x)叫做 Lagrange 余项。
欧拉方法
考虑一阶常微分方程的初值问题
前向欧拉方法
后向Euler算法或者后退Euler算法
梯形公式
改进的欧拉算法
其中,后向欧拉算法和梯形公式是隐式算法,前向欧拉算法和改进的欧拉算法是显式算法。欧拉算法计算容易,但是精度低,梯形公式精度高,但是是隐式形式,不易求解。将两式结合,则可以得到改进的欧拉公式。先用欧拉公式求出yn+1的一个粗糙的估计值,再用梯形方法进行精确化,称为校正值。
四阶龙格库塔算法(Runge-kutta method)
龙格-库塔算法是一种在工程上应用广泛的高精度单步算法,算法精度较高,如果预先取四个点就是四阶龙格-库塔算法。
欧拉方法和龙格-库塔算法的matlab实现
前向欧拉算法和后向欧拉算法
常微分方程y' = -y + x + 1;
x0 = 0; %时间起始
x1 = 30; %时间终止
h = 2.1; %间隔
y0 = 1; %初始值
代码:
%func.m文件 常微分方程为y' = -y + x + 1
function z = func(x, y)
z = -y + x + 1;
%forwardEuler.m文件
function [x, y] = forwardEuler(x0, y0, x1, h)
n = floor((x1 - x0)/h);
x = zeros(n + 1, 1);
y = zeros(n + 1, 1);
x(1) = x0;
y(1) = y0;
for i = 1 : n
x(i + 1) = x(i) + h;
y(i + 1) = y(i) + h * (-y(i) + x(i) + 1);
end
%backwardEuler.m文件
function [x, y] = backwardEuler(x0, y0, x1, h)
n = floor((x1 - x0)/h);
x = zeros(n + 1, 1);
y = zeros(n + 1, 1);
x(1) = x0;
y(1) = y0;
for i = 1 : n
x(i + 1) = x(i) + h;
y(i + 1) = 1/(1 + h) * (y(i) + h * x(i + 1) + h);
end
%命令
x0 = 0; %时间起始
x1 = 30; %时间终止
h = 2.1; %时间间隔
y0 = 1; %y起始值
[x, y] = forwardEuler(x0, y0, x1, h);
[p, q] = backwardEuler(x0, y0, x1, h);
hold on %将多个图均显示出来
plot(x, y,'r','LineWidth', 2)
plot(p, q, 'b','LineWidth', 2)
l = x0 : 0.01 : x1;
lu = exp(-l) + l;
plot(l, lu, 'g','LineWidth', 2)
legend('forwardEuler','backwardEuler','Theroy')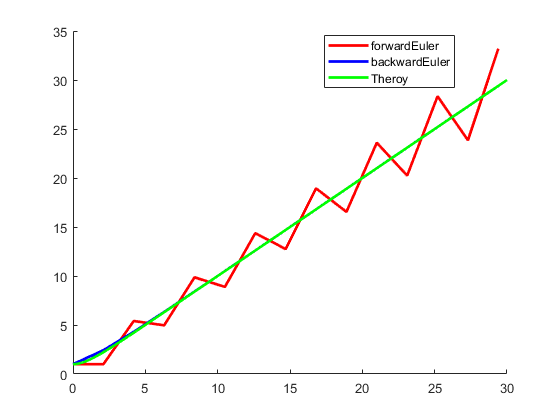
改进欧拉算法
常微分方程y' = y - 2x/y;
x0 = 0;
x1 = 1;
h = 0.1;
y0 = 1;
代码:
%常微分方程y' = y - 2x/y;
function z = func(x, y)
z = y - 2 * x / y;
useEuler.m文件 %向前欧拉算法代码
function [x, y] = useEuler(x0, x1, y0, h)
n = floor((x1 - x0)/h);
x = zeros(n + 1, 1);
y = zeros(n + 1, 1);
x(1, 1) = x0;
y(1, 1) = y0;
for i = 2 : n+1
x(i, 1) = x(i - 1, 1) + h;
y(i, 1) = y(i - 1, 1) + h * (y(i - 1, 1) - 2 * x(i - 1, 1) / y(i - 1, 1));
end
improvedEuler.m %改进的欧拉算法代码
function [x, y] = improvedEuler(x0, x1, y0, h)
n = floor((x1 - x0)/h);
x = zeros(n + 1, 1);
y = zeros(n + 1, 1);
x(1, 1) = x0;
y(1, 1) = y0;
for i = 2 : n+1
x(i, 1) = x(i - 1, 1) + h;
y(i, 1) = y(i - 1, 1) + h * (y(i - 1, 1) - 2 * x(i - 1, 1) / y(i - 1, 1));
y(i, 1) = y(i - 1, 1) + h / 2 * (y(i - 1, 1) - 2 * x(i - 1, 1) / y(i - 1, 1) + y(i, 1) - 2 * x(i, 1) / y(i, 1));%用上一步求得的值代入这一步,变为显式算法
end
untitle.m文件
x0 = 0;
x1 = 1;
y0 = 1;
h = 0.1;
[x, y] = useEuler(x0, x1, y0, h);
yy = sqrt(2 * x + 1); %精确解
[x, q] = improvedEuler(x0, x1, y0, h);
hold on
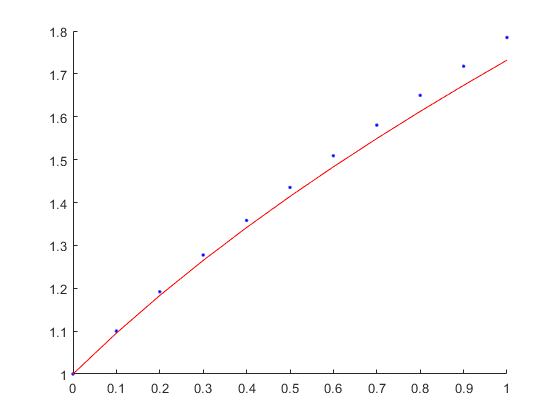
plot(x, y, 'b');
plot(x, yy, 'r');
plot(x, q, 'b.');结果:
常微分方程y' = (x - y)/2;
x0 = 0;
x1 = 3;
y0 = 1;
h = 0.25;
代码:
function [x, y] = runge(x0, x1, y0, h)
n = (x1 - x0) / h;
x = zeros(n + 1);
y = zeros(n + 1);
x(1) = x0;
y(1) = y0;
for i = 1:n
x(i + 1) = x(i) + h;
k1 = fun(x(i), y(i));
k2 = fun(x(i) + 0.5*h, y(i) + k1*h/2);
k3 = fun(x(i) + 0.5*h, y(i) + k2*h/2);
k4 = fun(x(i)+ h, y(i) + k3*h);
y(i + 1) = y(i) + h*(k1 + 2*k2 + 2*k3 + k4)/6;
end
end
function z = fun(x, y)
z = (x - y)/2;
end
x0 = 0;
x1 = 3;
y0 = 1;
h = 0.25;
[x, y] = runge(x0, x1, y0, h);
[p, q] = ode45(@fun, [0, 3], y0);
hold on
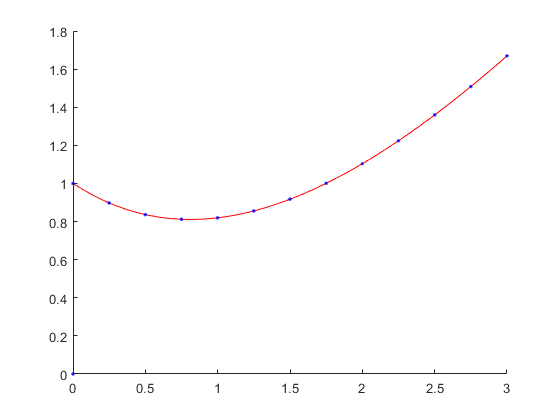
plot(p, q, 'r');
plot(x, y, 'b.');结果:
matlab中常用函数的总结
取整函数
floor函数朝负无穷方向取整,例如floor(-1.3) = -2, floor(2.8) = 2
ceil函数朝正无穷方向取整,例如ceil(1.2) = 2, ceil(-1.9) = -1
round函数 四舍五入, 例如round(3.3) = 3, round(-4.8) = -5
fix函数朝0方向取整, 例如fix(1.8) = 1, fix(-1.8) = -1
绘图时常用的函数
plot函数plot函数的常用的调用语法如下:
plot(Y),如果Y为实数向量,其维数为m,则plot(Y)等价于plot(X, Y), 其中X = 1:m。
例如,plot(t, y + 0.5)
plot(X1, Y1, X2, Y2.....),Xi和Yi成对出现,该函数分别按照顺序取两个数据Xi和Yi绘图。
plot(X1, Y1, LineSpec,...),将按顺序分别绘出由3个参数Xi、Yi和LineSpec定义的线条。其中参数LineSpec指明了线条的类型,再分别将配对的向量绘制出来。
例如,plot(x, y, axis('equal'), xlabel('x'), ylabel('y'))
曲线的线型和颜色参数
-, :, -., --,分别代表的是实线,虚线,点化线,双划线。
b, g, r, c, m, y, k, w,分别代表的是蓝,绿,红,青, 品红,黄,黑,白色。
hold on是当前轴及图形保持而不被刷新,准备接受此后的绘制。即在坐标轴内画了一个图后,再画另一个图时,原图还在,与新图共存;
hold off是使当前轴及图形不再具备被刷新的性质。即你在当前的坐标系中画了一幅图,此时的状态是hold off,则再画另一个图时,在轴上绘制的是新图,原图被替换了。
legend(S1, S2,...)绘制曲线所用线型、色彩或数据点型图例
subplot(m, n, p)或subplot(mnp), 子图函数所有的图按m行n列来排放,p表示该图所在的位置。








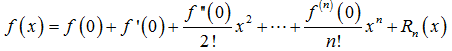
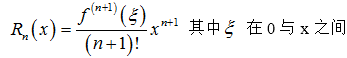
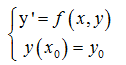
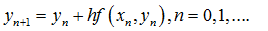
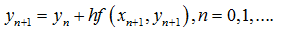
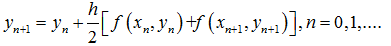
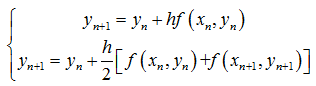
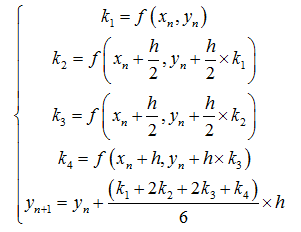














 876
876

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








