目录
前言
我们在第三章学了线性回归和softmax回归。这两个回归都只有一个输入层,一个输出层。这种并没有体现出深度学习的深度二字。
有了前面的基础,现在我们可以开始对深度神经网络的探索,神经网络的深度在这里体现。
那么好,我们现在开始。
一、隐藏层
1.1线性模型的局限性:
线性假设要求数据之间的关系必须是线性的,即输出必须是输入的线性组合。但在现实世界中,许多问题涉及非线性关系。
数据往往包含非线性结构,如曲线、簇状分布或交互作用。仿射变换只能创建直线或超平面决策边界,而非线性问题需要曲线边界。
而从模型的能力考量,softmax回归作为线性模型,其表达能力有限。如果数据不是线性可分的,即使加上softmax,也无法改变变换的线性本质。
所以,线性回归对于解决现实世界的问题,是远远不够的。
1.2加入隐藏层
书上的原话:我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制, 使其能处理更普遍的函数关系类型。最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到上面的层,直到生成最后的输出。
全连接层:相邻两层之间的所有神经元之间都有连接。如图:
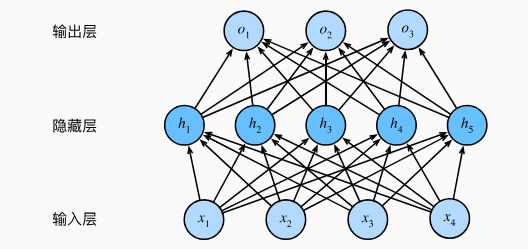
这种架构通常称为多层感知机,通常缩写为MLP。
因为输入层不进行计算,所以以上示例的多层感知机的层数为2。
1.3从线性到非线性
在添加影藏层后,模型现在需要跟踪和更新额外的参数。但是如果是我们隐藏层添加的仍然是仿射变换,那么这个跟踪和更新是毫无意义的。
因为仿射变换的仿射变换,仍然是仿射变换。
多加的几层,完全可以用一层来实现。如下图,H是隐藏层计算,O是输出层计算。
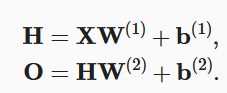
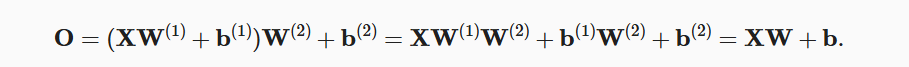
经过数学计算,最后O的形式仍然是XW+b,一个仿射变换就可以实现,为什么要用多几层来增加计算量呢?
所以,为了发挥多层的意义,我们还需要一个额外的关键要素: 在仿射变换之后对每个隐藏单元应用非线性的激活函数。
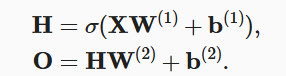
为了构建更通用的多层感知机, 我们可以继续堆叠这样的隐藏层,直到功能更强大,表现力更强的模型。
二、激活函数
激活函数是加在神经网络神经元输出上的一个非线性函数。它的主要目的是为神经网络引入非线性变换。
以下是常见的激活函数:
2.1ReLU函数
![]()
因为它实现简单,同时在各种预测任务中表现良好。所以也是最受欢迎的激活函数。
以下的代码就不说了,都用过很多次了。
import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'True'
import torch
import matplotlib.pyplot as plt
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
# 使用 matplotlib 绘制图形
plt.figure(figsize=(5, 2.5))
plt.plot(x.detach().numpy(), y.detach().numpy())
plt.xlabel('x')
plt.ylabel('relu(x)')
plt.title('ReLU Activation Function')
plt.grid(True)
plt.show()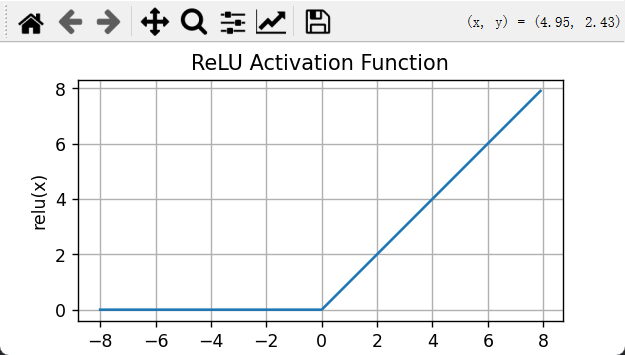
ReLU的导数也很简单,当输入为负时,ReLU函数的导数为0,而当输入为正时,ReLU函数的导数为1。
注意,这个函数在0点不可导,所以默认导数为0。我们可以忽略这种情况,因为输入可能永远都不会是0。
y.backward(torch.ones_like(x), retain_graph=True)
plt.figure(figsize=(5, 2.5))
plt.plot(x.detach().numpy(), x.grad.numpy())
plt.xlabel('x')
plt.ylabel('grad of relu')
plt.grid(True)
plt.show()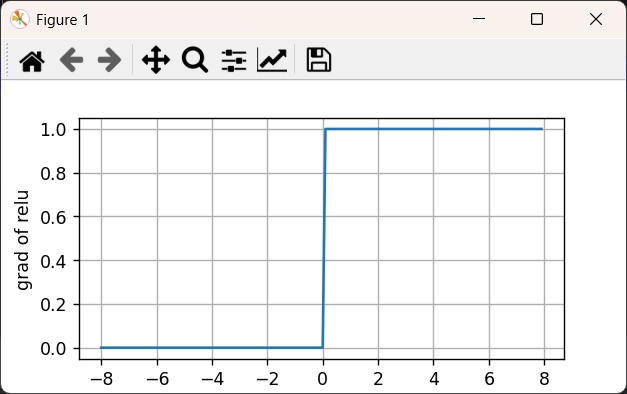
书上原文:
使用ReLU的原因是,它求导表现得特别好:要么让参数消失,要么让参数通过。 这使得优化表现得更好,并且ReLU减轻了困扰以往神经网络的梯度消失问题(稍后将详细介绍)。
2.2sigmoid函数
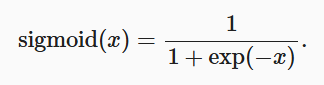
应用场景:当我们想要将输出视作二元分类问题的概率时, sigmoid仍然被广泛用作输出单元上的激活函数。
二元分类,就是非此即彼,一堆图片,只有两个标签,{猫,狗},输出不是猫就是狗。
目前,sigmoid在隐藏层中已经较少使用, 它在大部分时候被更简单、更容易训练的ReLU所取代。
在后面关于循环神经网络的章节中,我们将描述利用sigmoid单元来控制时序信息流的架构。
我们也可以汇出它和它导数的图形:
sigmoid函数:
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.sigmoid(x)
plt.figure(figsize=(5, 2.5))
plt.plot(x.detach().numpy(), y.detach().numpy())
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.grid(True)
plt.show()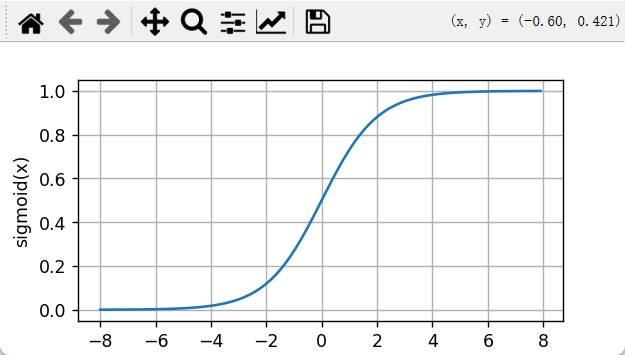
sigmoid导数:(注意,如果之前求过x的梯度,得把x的梯度清零)
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
plt.figure(figsize=(5, 2.5))
plt.plot(x.detach().numpy(), x.grad.numpy())
plt.xlabel('x')
plt.ylabel('grad of sigmoid')
plt.grid(True)
plt.show()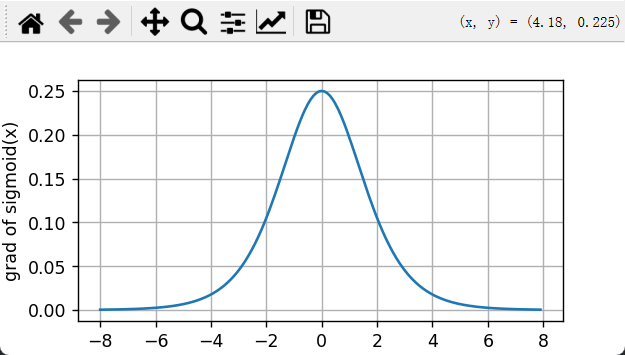
2.3tanh函数
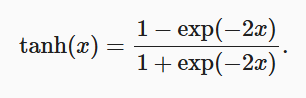
书中原话:当输入在0附近时,tanh函数接近线性变换。 函数的形状类似于sigmoid函数, 不同的是tanh函数关于坐标系原点中心对称。
y = torch.tanh(x)
plt.figure(figsize=(5, 2.5))
plt.plot(x.detach().numpy(), y.detach().numpy())
plt.xlabel('x')
plt.ylabel('tanh(x)')
plt.grid(True)
plt.show()
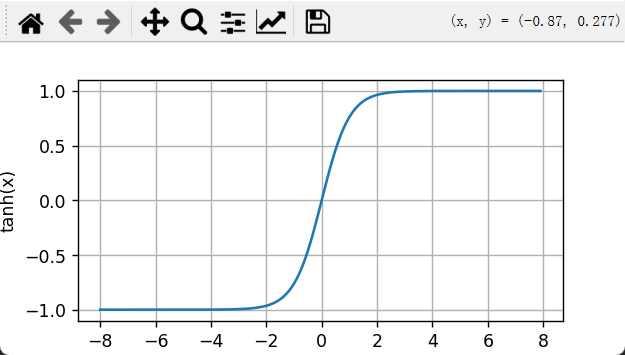
用数学的方法,很容易求出来它的导数:
当输入接近0时,tanh函数的导数接近最大值1。 与我们在sigmoid函数图像中看到的类似, 输入在任一方向上越远离0点,导数越接近0。
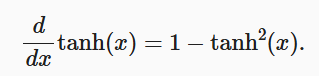
x.grad.zero()
y.backward(torch.ones_like(x),retain_graph=True)
plt.figure(figsize=(5, 2.5))
plt.plot(x.detach().numpy(), x.grad.numpy())
plt.xlabel('x')
plt.ylabel('grad of tanh(x)')
plt.grid(True)
plt.show()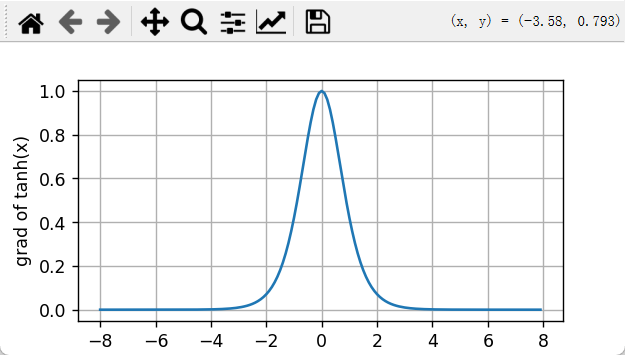
tanh的主要应用场景:
-
RNN家族网络(LSTM/GRU)
-
输出需要限制在[-1,1]范围的场景
-
需要零中心化激活值的网络
-
对梯度消失敏感但又不适合ReLU的场景




















 575
575

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








