第 9 章 数据的决策分析及可视化

9.1 确定性分析

9.1.1 单目标求解及图示

（1）读取数据

import pandas as pd
Tv=pd.read_excel('./data/DaPy_data.xlsx','Target',index_col=0)
Tv #目标值 

（2）计算年收益金额

Tv['年收益']=Tv.年销售量*(Tv.销售单价-Tv.单件成本)-Tv.设备投资
Tv 

（3）年收益的直观分析

import matplotlib.pyplot as plt            
plt.rcParams['font.sans-serif']=['SimHei']
#plt.rcParams['figure.dpi']=90  #分辨率
Tv['年收益'].plot(kind='bar')

（4）确定最佳方案：收益率最大者为最佳方案。

Tv['年收益'].idxmax()

9.1.2 多目标求解及图示

（1）计算理想值:

Ev=[min(Tv.设备投资), min(Tv.单件成本), max(Tv.年销售量), max(Tv.销售单价), max(Tv.年收益)]
Ev #理想值 

（2）计算差距: 

Tv_Ev2=((Tv-Ev))**2    #差值的平方 
Tv_Ev2

Dv=(Tv_Ev2).sum(1)
Dv   #差距

Tv['差距']=Dv
Tv

（3）差距的直观分析

Dv.plot(kind='bar');

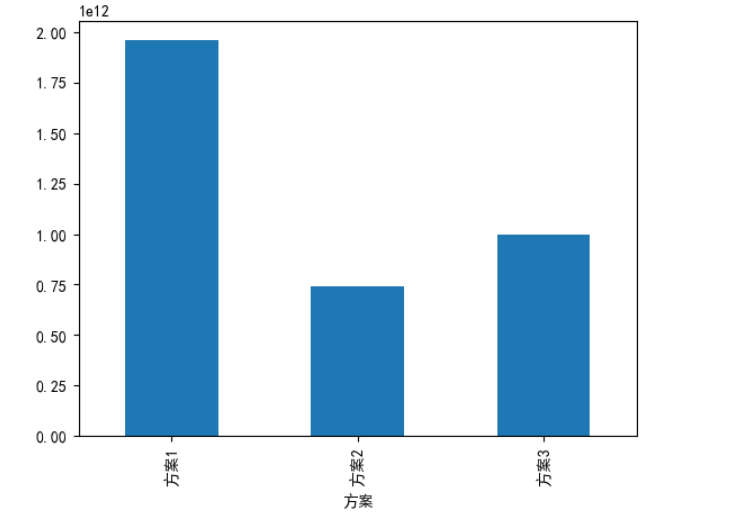
（4）确定最佳方案

Dv.idxmin() 

pd.DataFrame({'单目标':Tv['年收益'],'单目标方案':Tv['年收益']==Tv['年收益'].max(),
              '多目标':Tv['差距'],'多目标方案':Tv['差距']==Tv['差距'].min()})

9.2 不确定性决策分析

9.2.1 分析方法简介

PLm=pd.DataFrame();    #构建损益矩阵 ProfitLoss matrix 
PLm['畅销']= 12000*(Tv.销售单价-Tv.单件成本)-Tv.设备投资; 
PLm['一般']= 8000*(Tv.销售单价-Tv.单件成本)-Tv.设备投资; 
PLm['滞销']= 1500*(Tv.销售单价-Tv.单件成本)-Tv.设备投资;
PLm 

9.2.2 不确定分析原则

9.2.2.1 乐观原则

lg=PLm.max(axis=1)
lg  #每列最大者

BQD=PLm.copy()
print(PLm)
BQD['乐观']=lg
print(BQD)

lg.plot(kind='bar')

lg.idxmax() 

9.2.2.2 悲观原则

bg=PLm.min(1)
bg

BQD['悲观']=bg
BQD

plt.rcParams['axes.unicode_minus']=False;  #正常显示图中负号
bg.plot(kind='bar')

bg.idxmax() 

9.2.2.3 折中原则

a=0.35 
zz= a*lg + (1-a)*bg
zz

BQD['折中']=zz
BQD

zz.plot(kind='bar')

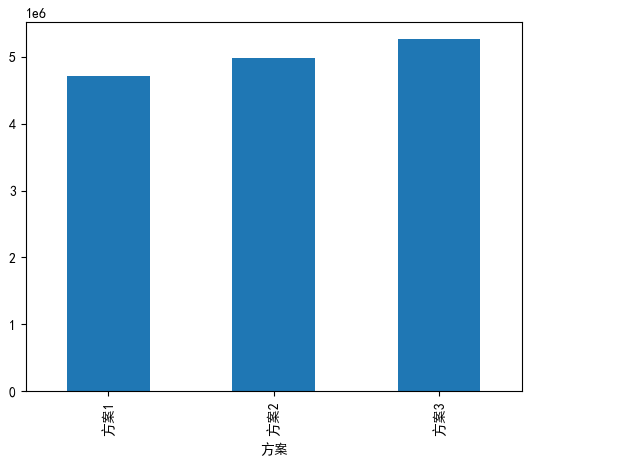
zz.idxmax() 

9.2.2.4 后悔原则

Rm=PLm.max()-PLm
Rm  #构建后悔矩阵 Regret matrix 

hh=Rm.max(1)
hh 

BQD['后悔']=hh
BQD

hh.plot(kind='bar')

hh.idxmin() 

pd.DataFrame({'乐观':lg,'乐观方案':lg==lg.max(),'悲观':bg,'悲观方案':bg==bg.max(),
              '折中':zz,'折中方案':zz==zz.max(),'后悔':hh,'后悔方案':hh==hh.min()})

9.3 概率型风险分析

9.3.1 期望值法及直观分析

probE=[0.1,0.65,0.25]  #初始概率 
qw=(probE*PLm).sum(1)
qw

qw.plot(kind='bar')

qw.idxmax()

9.3.2 后悔期望值法及直观分析

Rm

probE=[0.1,0.65,0.25]
hhqw=(probE*Rm).sum(1)
hhqw

hhqw.plot(kind='bar')

hhqw.idxmin()

pd.DataFrame({'期望值':qw,'期望方案':qw==qw.max(),
              '后悔期望值':qw,'后悔期望方案':hhqw==hhqw.min()})