Leetcode刷题笔记—array （10）

462. Minimum Moves to Equal Array Elements II

class Solution:
    def minMoves2(self, nums: List[int]) -> int:
        res = 0
        nums.sort()
        median = nums[len(nums) // 2]
        for num in nums:
            if num == median:
                continue
            res += abs(num - median)
        return res

        '''
        中位数是使得一组数到这个点的距离总和最小的点。
        这是一个统计学上的结论，用在这个问题上，
        意味着如果我们将数组中的所有数都调整到中位数，所需的操作次数是最少
        '''

        

453. Minimum Moves to Equal Array Elements

class Solution:
    def minMoves(self, nums: List[int]) -> int:
        min_ele = min(nums) # 找到数组中的最小元素
        # calculate the sum of difference between each ele and the min ele
        sum_diff = sum(nums) - len(nums) * min_ele
        return sum_diff

        '''
        通过反转思维，将所有元素变为相等的最小值所需的操作次数，
        等价于将数组中的所有元素减到等于最小值的操作次数。
        每次将 n-1 个元素增加1，等价于将剩下的那个元素减少1。
        最终需要的操作次数就是所有元素与最小值的差值之和
        '''
        

740. Delete and Earn

class Solution {
    public int deleteAndEarn(int[] nums) {
        // nums[i]<= 10000，将nums中每个数字出现的次数记录下来，
        int number[] = new int[10001];
        // 前一个数字包含和不包含情况
        int include = 0, exclude =0;
        // 记录出现次数
        for(int num : nums) {
            number[num]++;
        }
        for(int i = 0; i < 10001; i++) {
            int curInclude = number[i] * i + exclude;
            // 不包含取前面include和exclude中的最大值，因为前面一个数也是可取 
            // 可不取的 我们需要的是最大值即可
            int curExclude = Math.max(include, exclude);
            include = curInclude;
            exclude = curExclude;
        }
        return Math.max(include, exclude);
    }
}

229. Majority Element II 默尔投票

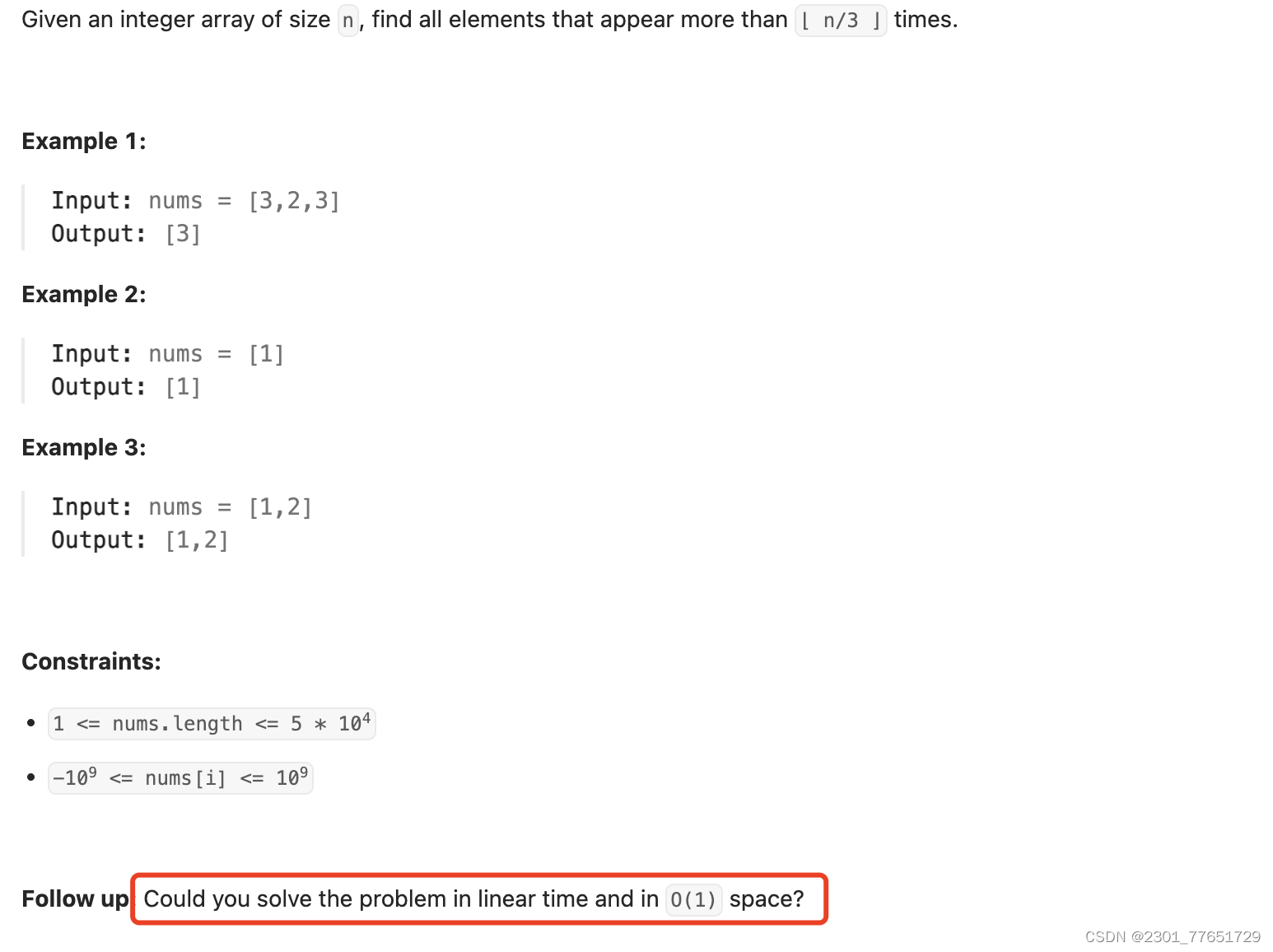
class Solution {
    public List<Integer> majorityElement(int[] nums) {
        /*  Boyer-Moore Majority Voting Algorithm.
    This algorithm can be used to return the highest K elements that appeared in the array more than array_size/(K+1) times. In our case, K = 2.
    he major Intuition behind this algorithm is that maintaining voting variable for the candidates:
    Increase the variable if you faced the candidate in your iteration.
    Decrease the variable if you faced another element.
    If the variable reaches 0, look for another promising candidate.
    1. Boyer-Moore Majority Voting Solution
    Create variables to track counts and candidates for potential majority elements.
    First Pass - Find Potential Majority Elements:
    Iterate through the input array and identify potential majority element candidates.
    Update the candidates based on specific conditions.
     Maintain counts for each candidate.
    Second Pass - Count Occurrences:
    Iterate through the input array again to count the occurrences of the potential majority elements.
    Compare the counts with a threshold to determine the majority elements.
    Return Majority Elements.
Since we are iterating over the array in two passes then the complexity is 2 * N which is O(N).
Space complexity: O(1)O(1)O(1)
Since we are only storing constant variables then the complexity is O(1).
*/
int count1 = 0, count2 = 0; // Counters for the potential majority elements
        int candidate1 = 0, candidate2 = 0; // Potential majority element candidates

        // First pass to find potential majority elements.
        for (int i = 0; i < nums.length; i++) {
            // If count1 is 0 and the current number is not equal to candidate2, update candidate1.
            if (count1 == 0 && nums[i] != candidate2) {
                count1 = 1;
                candidate1 = nums[i];
            } 
            // If count2 is 0 and the current number is not equal to candidate1, update candidate2.
            else if (count2 == 0 && nums[i] != candidate1) {
                count2 = 1;
                candidate2 = nums[i];
            } 
            // Update counts for candidate1 and candidate2.
            else if (candidate1 == nums[i]) {
                count1++;
            } else if (candidate2 == nums[i]) {
                count2++;
            } 
            // If the current number is different from both candidates, decrement their counts.
            else {
                count1--;
                count2--;
            }
        }

        List<Integer> result = new ArrayList<>();
        int threshold = nums.length / 3; // Threshold for majority element

        // Second pass to count occurrences of the potential majority elements.
        count1 = 0;
        count2 = 0;
        for (int i = 0; i < nums.length; i++) {
            if (candidate1 == nums[i]) {
                count1++;
            } else if (candidate2 == nums[i]) {
                count2++;
            }
        }

        // Check if the counts of potential majority elements are greater than n/3 and add them to the result.
        if (count1 > threshold) {
            result.add(candidate1);
        }
        if (count2 > threshold) {
            result.add(candidate2);
        }

        return result;
    }
}

169. Majority Element

class Solution {
    public int majorityElement(int[] nums) {
        int n = nums.length;
        Map<Integer, Integer> map = new HashMap();
        for(int i = 0; i < n; i++) {
            map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
        }
        for(Map.Entry<Integer, Integer> entry: map.entrySet()){
            if(entry.getValue() > n / 2) {
                return entry.getKey();
            }
        }
        return 0;
    }
}

162. Find Peak Element

class Solution {
    public int findPeakElement(int[] nums) {
        // 找到mid元素，基于local找peak值
        // 基于mid，两种情况：mid + 1 大于 mid 则left变为 mid + 1，
        // mid + 1 小于 mid peak值在左边，right变成 mid — 1
        int left = 0, right = nums.length - 1;
        while(left < right) {
            int mid = left + (right - left) / 2;
            if(nums[mid] < nums[mid + 1]) {
                left = mid + 1;
            } else {
                right = mid; // 右边呈下降趋势时，mid有可能是peak，所以right不能为mid - 1；
            }
        }
        return left;
    }
}

66. Plus One

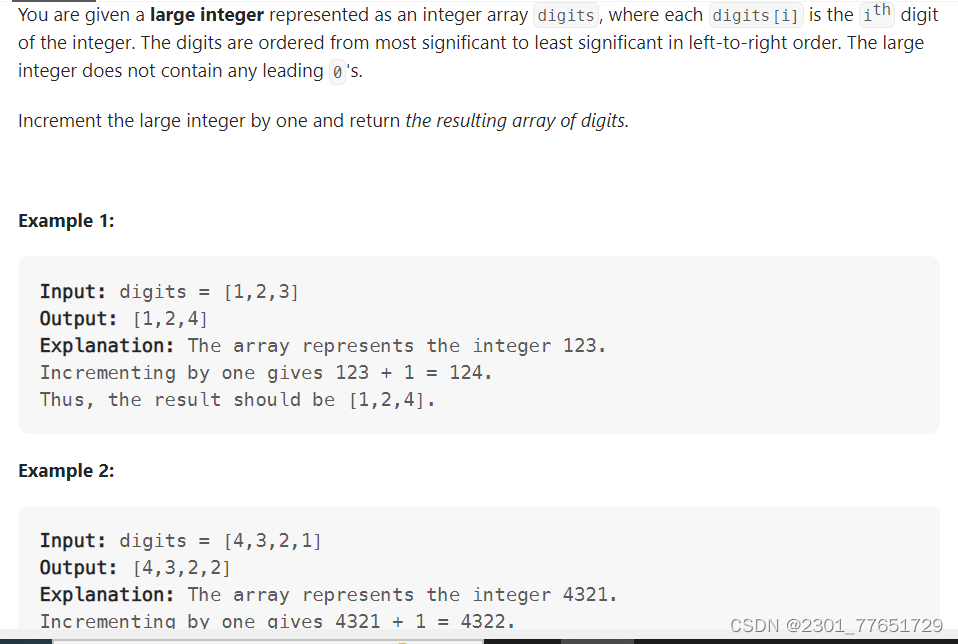
class Solution {
    public int[] plusOne(int[] digits) {
       for(int i = digits.length - 1; i >= 0; i--) {
           if(digits[i] < 9) {
               digits[i]++;
               return digits;
           }
           digits[i] = 0;
       } 
       digits = new int[digits.length + 1];
       digits[0] = 1;
       return digits;
    }
}

58. Length of Last Word 

class Solution {
    public int lengthOfLastWord(String s) {
       s = s.trim(); //用于去除字符串两端的空白字符（例如空格、制表符、换行符等）
                    //这个操作通常返回一个新的字符串，其中移除了原始字符串开头和结尾的空格。
       int count = 0;
       for(int i = s.length() - 1; i >= 0; i--) {
           if(s.charAt(i) != ' ') {
               count++;
           } else {
               break;
           }
       }
       return count;
    }
}

389. Find the Difference

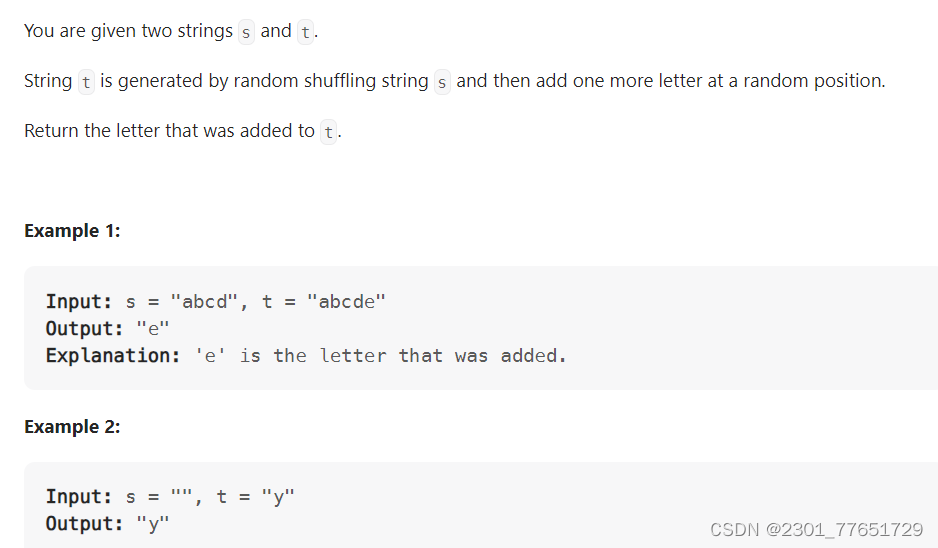
class Solution {
    public char findTheDifference(String s, String t) {
       char c = 0;
       for(char cs : s.toCharArray()) {
           c ^= cs; 
// 任何数与0进行异或操作都会保持不变（A XOR 0 = A）
//任何数与0进行异或操作都会保持不变：A XOR 0 = A
//任何数与自身进行异或操作的结果为0：A XOR A = 0
//异或运算是可交换的：A XOR B = B XOR A
       }
       for(char ct : t.toCharArray()) {
           c ^= ct;
       }
       return c;
    }
}



class Solution {
    public char findTheDifference(String s, String t) {
       int[] ch = new int[26];
       for(char cs : s.toCharArray()) {
           ch[cs - 'a']++;
       }
       for(char ct : t.toCharArray()) {
           ch[ct - 'a']--;
       }
       for(int i = 0; i < 26; i++) {
           if(ch[i] < 0) {
               return (char) (i + 'a');
           }
       }
       return ' ';
    }
}

268. Missing Number 

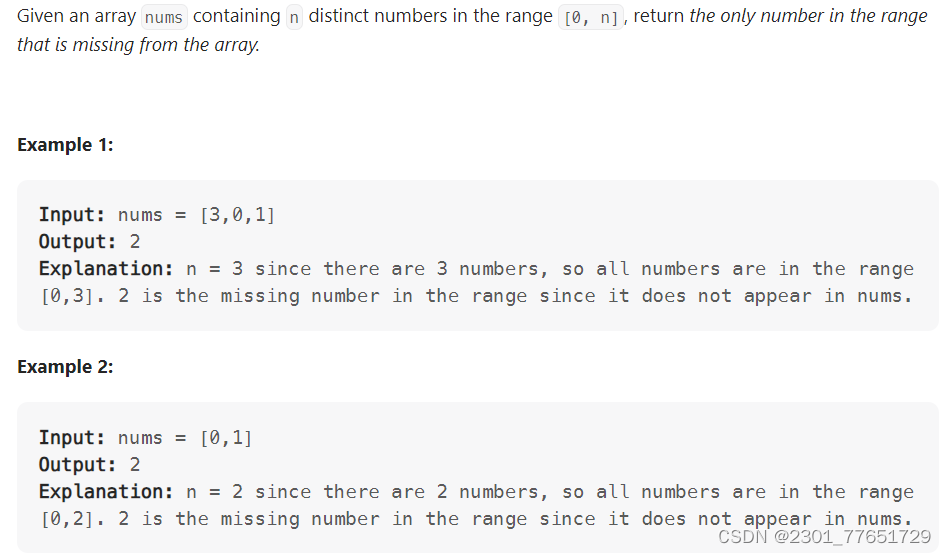
class Solution {
    public int missingNumber(int[] nums) {
        int num = 0;
        for(int i = 0; i < nums.length; i++) {
            num += i + 1 - nums[i];
        }
        return num;
    }
}