约瑟夫环问题

1.输出出圈人序号

 

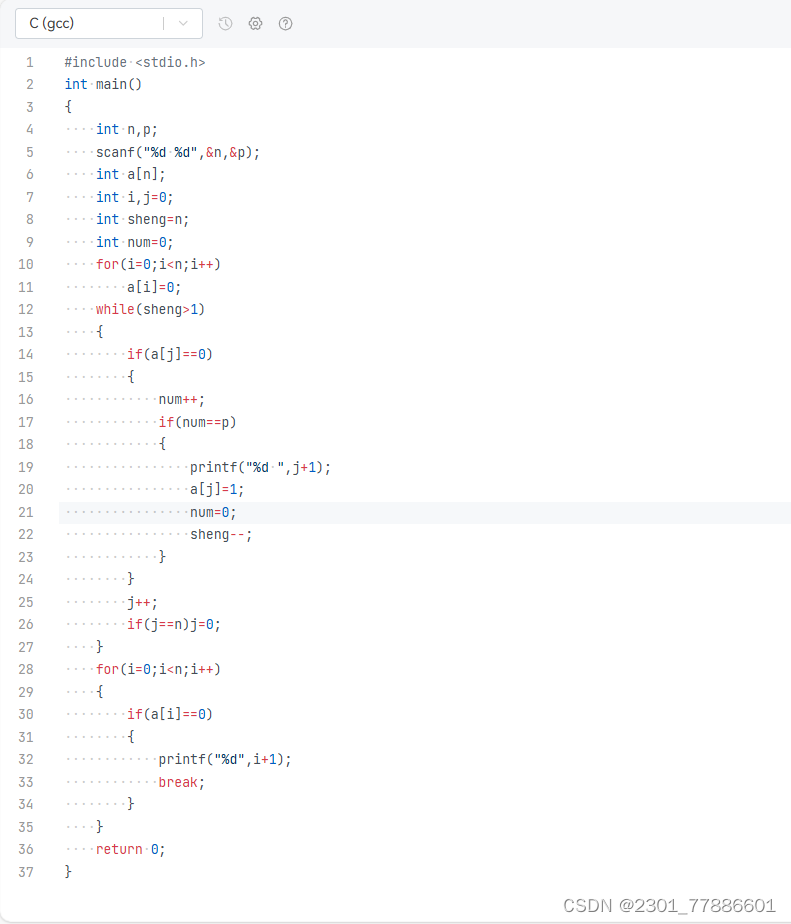
 2.猴子选大王（输出最后一个剩余的猴）

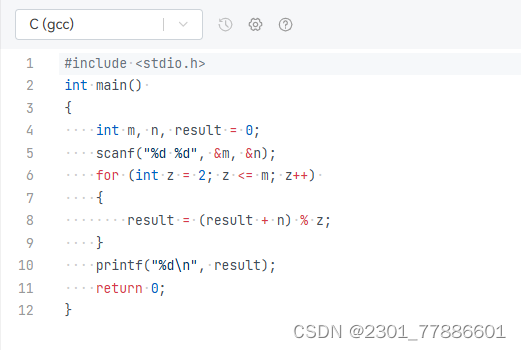
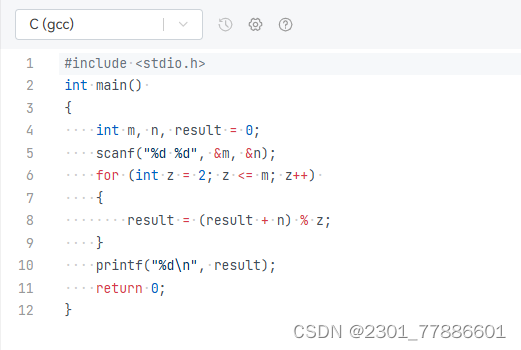 这是基于约瑟夫环问题的数学推导思路。假设初始有  n  个猴子（对应代码里输入的第一个数，也就是猴子总数），每次报数到  m  （对应代码里输入的第二个数，报数的数字）的猴子出圈。
 
可以通过逐步推导来理解，当只有1只猴子时，那这只猴子就是最后的“猴王”，编号为0。当有2只猴子时，经过一轮报数（报数到  m  的出圈），剩下那只猴子的编号就可以通过计算  (0 + m) % 2  得出（这里的0是上一轮（只有1只猴子时）剩下猴子的编号）。
 
随着猴子数量不断增多，比如有  z  只猴子时（ z  从2逐步递增到  n ），每一轮都可以根据上一轮剩下猴子的编号按照  (上一轮编号 + m) % 当前猴子总数  这样的规律来计算这一轮剩下猴子的编号，不断递推下去，最后得出的  result  就是经过多轮报数后剩下那只猴子（猴王）在初始  n  只猴子中的编号。