C++二叉搜索树

已于 2024-03-28 21:41:50 修改
阅读量1k 收藏 28
点赞数 10
分类专栏： C++修炼之路 文章标签： c++ 开发语言
于 2024-03-24 23:09:17 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2301_77934192/article/details/136590003
版权

💓博主CSDN主页:麻辣韭菜-CSDN博客💓
 
⏩专栏分类：C++知识分享⏪
 
🚚代码仓库:C++高阶🚚
 
🌹关注我🫵带你学习更多C++知识
  🔝🔝

目录

一.二叉搜索树的定义

二. 二叉搜索树循环操作

1. 二叉搜索树的插入

2. 二叉搜索树的查找

3. 二叉搜索树的删除

三.二叉搜索树递归操作

1.二叉搜索树递归算法的插入实现

2.二叉搜索树递归算法的查找实现

3.二叉搜索树递归算法的删除实现

四.二叉搜索树拷贝构造（赋值重载）与析构函数

五.二叉搜索树应用场景

1. K模型

2. KV模型

3.二叉搜索树的性能分析

一.二叉搜索树的定义

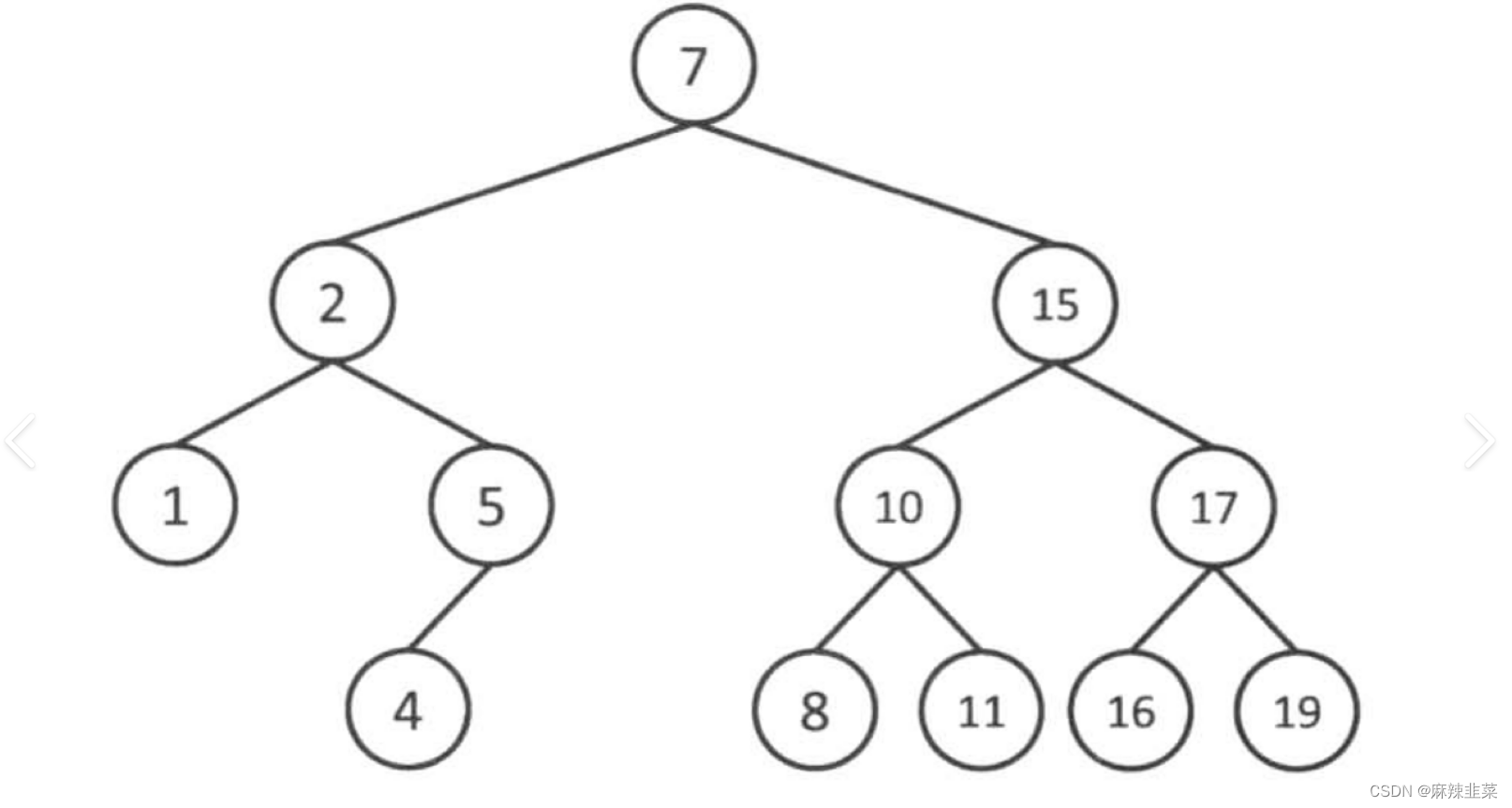
观察上图，我们可以发现根节点7的左边节点是小于右边的节点，左子树的上所有的节点都小于根节点，右子树的所有节点都大于根节点。而且根的左右子树也都是搜索二叉树

二. 二叉搜索树循环操作

1. 二叉搜索树的插入

先定义出二叉搜索树结构 

//定义二叉树节点
template<class K>
struct BSTreeNode
{
	BSTreeNode* _left;
	BSTreeNode* _right;
	K _key;
	BSTreeNode(const K& key)
		:_left(nullptr)
		,_right(nullptr)
		,_key(key)
	{}
	
};
template<class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
public:
private:
	Node* _root = nullptr;

};

二叉搜索树插入实现方法↓

public:
    //二叉搜索树插入实现
	bool Insert(const K& key)
	{
		if (_root == nullptr) //第一次就不用说了。
		{
			_root = new Node(key);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key) //小于要插入的数就在右子树
			{	
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key) //大于要插入的数就在左子树
			{
				parent = cur;
				cur = cur->_left;
			}
			else  // 相等后面AVL 红黑在说。
			{
				return false;
			}

		}
		cur = new Node(key);
		//链接
		if (parent->_key < key)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		return true;
	}

这里有个细节必须要说以下记录下父节点，cur出了作用域就销毁了，我们在链接过程中是找不到cur，就存在内存泄漏了野指针问题。先编写个中序遍历函数打印看看是不是对的

//中序遍历函数
void Inorder() 
	{
		_InOrder(_root);
		cout << endl;
	}
	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;
		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}

我们在主函数中，调中序函数传参是个问题，我们在类的内部再实现一个调用中序遍历的函数。

打印结果没有问题，接着实现查找和删除

2. 二叉搜索树的查找

bool Find(const K& key)
	{
		if (_root == nullptr) //如果二叉树为空直接返回假
		{
			return false;
		}
		Node* cur = _root;
		while (cur)//遍历左右子树
		{
			if (cur->_key < key) // 根小于要查找数右子树找
			{
				cur = cur->_right;
			}
			else if (cur->_key > key) // 根大于要查找数左子树找
			{
				cur = cur->_left;
			}
			else    //等于就是找到了 返回真
			{
				return true;
			}
		}
		return false; //循环结束没找到返回假
	}

3. 二叉搜索树的删除

删除比较复杂，先画图考虑各种左右子树情况

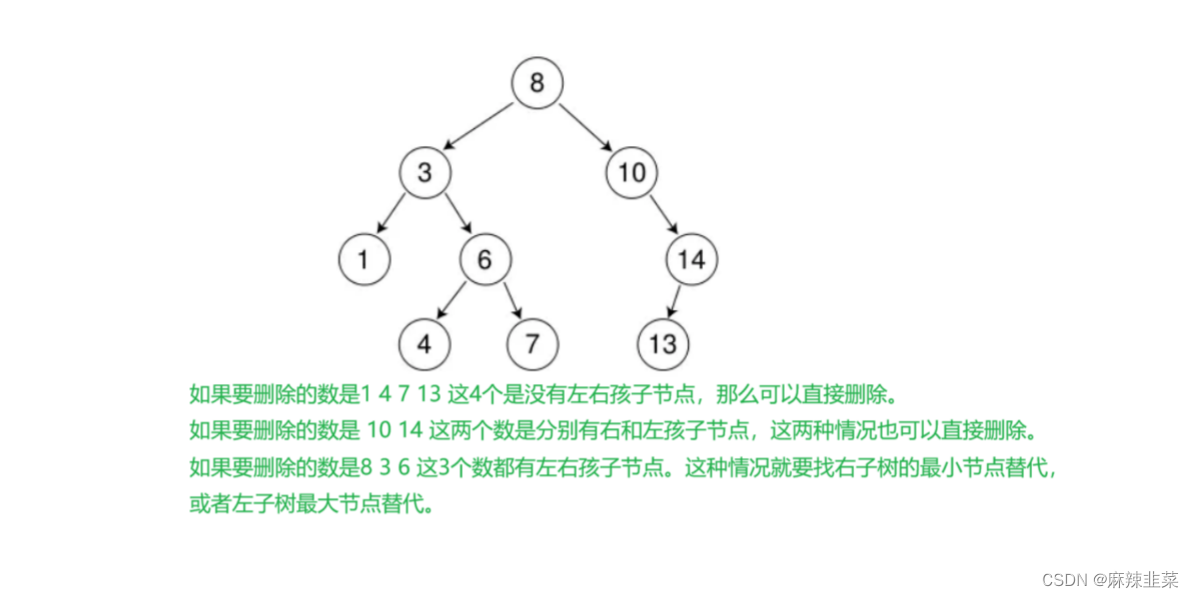
删除1 4 7 13 10 14 这6个数没有问题，直接无脑删除 父节点的左右指针指向nullptr就行。

问题的关键在于如何删除 8 3 6 这3个数？

替换法 比如 我要删除8 那就去左子树找到最大的那个节点 7。

把8修改成7 再删除7 这样就没有破坏二叉搜索树的结构。

bool Earse(const K& key)
	{
		if (_root == nullptr)
			return false; //树为空直接返回
		//遍历找到要删除的数
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else  //删除
			{
				//左为空
				if (cur->_left == nullptr)
				{
					if (cur == _root) //如果左子树全部为空，这时如果删除根节点，根节点是没有父亲节点。下面判断就是空指针。
					{
						_root = cur->_right;
					}
					else
					{
						if (parent->_left == cur)
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}
					delete cur;
				}
				//右为空
				else if (cur->_right == nullptr)
				{
					if (cur == _root) //同理左子树
					{
						_root = cur->_left;
					}
					else
					{
						if (parent->_left == cur)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
					}
					delete cur;
				}
				//两边都不为空 选择右子树小的节点或者左子树最大的节点。
				//以左子树最大节点为例
				else
				{
					Node* pmaxLeft = cur; //如果最大左子树的父亲节点设置为空，下面循环没有进去，父亲没有更新，下面条件判断就会出现空指针问题。
					Node* maxLeft = cur->_left;
					while (maxLeft->_right)
					{
						pmaxLeft = maxLeft;
						maxLeft = maxLeft->_right;
					}
					cur->_key = maxLeft->_key;
					if (pmaxLeft->_right == maxLeft) //这判断也是一样 如果上面循环没有进去 那么 8这个节点右子树就打乱结构了。
					{
						pmaxLeft->_right = maxLeft->_left;
					}
					else
					{
						pmaxLeft->_left = maxLeft->_left;
					}

					delete maxLeft;
					
				}
				return true;
			}
		}
		return false;
	}

三.二叉搜索树递归操作

1.二叉搜索树递归算法的插入实现

    bool InsertR(const K& key)
	{
		return _InsertR(_root, key);
	}
	bool _InsertR(Node* &root, const K& key)
	{
		if (root == nullptr)
			root = new Node(key);
		
		if (root->_key < key)
		{
			return _InsertR(root->_right, key);
		}
		else if (root->_key > key)
		{
			return _InsertR(root->_left, key);
		}
		else
		{
			return false;
		}
		
		
	}

用递归算法插入，这里有个小细节，我们在类内部实现是需要再套一层函数如上图代码所示

套的那层实现递归算法。如果我们要插入的值大于根的值那就往右子树递归，反之就往左子树递归。一直递归到空，在空这里new一个节点，关键的来了，如果我们传参的值不是引用，那么函数递归返回 栈帧销毁，新开的节点，在上一层递归函数父亲节点没有连接的。

我们传参时用引用就非常巧妙，引用本来就是它自己，父节点的右或左都是它，天然连接。

2.二叉搜索树递归算法的查找实现

    bool FindR(const K& key)
	{
		return _FindR(_root, key);
		
	}
	bool _FindR(Node* root ,const K& key)
	{
		if (root == nullptr)
			return false;
		if (root->_key == key)
			return true;
		else if(root->_key < key)
			return _FindR(root->_right, key);
		else
			return _FindR(root->_left, key);
	}

递归查找就非常简单了，大于就右边找，反之左边找，找到返回真，递归到空还是没有返回假，或者本来就是空。

3.二叉搜索树递归算法的删除实现

bool EraseR(const K& key)
	{
		return _EraseR(_root, key);
	}

	bool _EraseR(Node*& root, const K& key)
	{
		if (root == nullptr)
			return false;
		//小于根就左边找
		if (root->_key > key)
		{
			return _EraseR(root->_left, key);
		}
		//大于根就右边找
		else if (root->_key < key)
		{
			return _EraseR(root->_right, key);
		}
		//相等
		else
		{	//删除
			
			Node* del = root; //先记录要删除的节点，
            //右为空直接删除			
            if (root->_right == nullptr)
				root = root->_left;
			//左为空直接删除
            else if (root->_left == nullptr)
				root = root->_right;
			
            //两边都不为空，以右子树为例 找最小的            
            else
			{
				Node* MinRight = root->_right;
				while (MinRight->right)
				{
						MinRight = MinRight->left; //找到右边最小的节点
				}
				swap(root->_key, MinRight->_key);//替换法：右边节点最小的值和根交换值
				return _EraseR(root->_right, key);//替换了之后我们要删除就是它，
                //我们再次递归是不是就变成了上面两种情况，左右各为空的情况。
			}
			delete del;
			return true;
		}
	}

递归算法删除的实现 我直接在代码讲解了。有那个地方不懂得可以私信我

四.二叉搜索树拷贝构造（赋值重载）与析构函数

    BSTree() = default; // 制定强制生成默认构造
	BSTree(const BSTree<K>& k)
	{
		_root = Copy(k._root);
	}
	//现代拷贝写法
	BSTree<K>& operator=(BSTree<K> t)
	{
		swap(_root, t._root);
		return *this;
	}

	~BSTree()
	{
		Destroy(_root);
	}
    //构造
    Node* Copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;

		Node* newRoot = new Node(root->_key);
		newRoot = Copy(root->_left);
		newRoot = Copy(root->_right);
		return newRoot;
	}
    //析构
	void Destroy(Node* &root)
	{
		if (root == nullptr)
			return;
		Destroy(root->_left);
		Destroy(root->_right);
		delete root;
		root = nullptr;
	}

这3个默认成员函数这里不在多讲 ，不太理解的可以先看C++类和对象-CSDN博客。对于递归算法不太理解，自己可以下去多画一画递归展开图

五.二叉搜索树应用场景

1. K模型

K 模型即只有 key 作为关键码，结构中只需要存储 Key 即可，关键码即为需要搜索到
的值 。
比如： 给一个单词 word ，判断该单词是否拼写正确 ，具体方式如下：
以词库中所有单词集合中的每个单词作为 key ，构建一棵二叉搜索树
在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。

2. KV模型

每一个关键码 key ，都有与之对应的值 Value ，即 <Key, Value> 的键值对 。
该种方式在现实生活中非常常见：
比如 英汉词典就是英文与中文的对应关系 ，通过英文可以快速找到与其对应的中文，英
文单词与其对应的中文 <word, chinese> 就构成一种键值对；
再比如 统计单词次数 ，统计成功后，给定单词就可快速找到其出现的次数， 单词与其出
现次数就是 <word, count> 就构成一种键值对 。

 先讲之前K模型改造成KV模型

namespace gx
{
	template<class K, class V>
	struct BSTreeNode
	{
		BSTreeNode<K, V>* _left;
		BSTreeNode<K, V>* _right;
		K _key;
		V _value;

		BSTreeNode(const K& key, const V& value)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
			, _value(value)
		{}

	};
	template<class K, class V>
	class BSTree
	{
		typedef BSTreeNode<K, V> Node;
	public:
		
		
		bool Erase(const K& key)
		{
			if (_root == nullptr)
				return false; //树为空直接返回
			//遍历找到要删除的数
			Node* cur = _root;
			Node* parent = nullptr;
			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else  //删除
				{
					//左为空
					if (cur->_left == nullptr)
					{
						if (cur == _root) //如果左子树全部为空，这时如果删除根节点，根节点是没有父亲节点。下面判断就是空指针。
						{
							_root = cur->_right;
						}
						else
						{
							if (parent->_left == cur)
							{
								parent->_left = cur->_right;
							}
							else
							{
								parent->_right = cur->_right;
							}
						}
						delete cur;
					}
					//右为空
					else if (cur->_right == nullptr)
					{
						if (cur == _root) //同理左子树
						{
							_root = cur->_left;
						}
						else
						{
							if (parent->_left == cur)
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;
							}
						}
						delete cur;
					}
					//两边都不为空 选择右子树小的节点或者左子树最大的节点。
					//以左子树最大节点为例
					else
					{
						Node* pmaxLeft = cur; //如果最大左子树的父亲节点设置为空，下面循环没有进去，父亲没有更新，下面条件判断就会出现空指针问题。
						Node* maxLeft = cur->_left;
						while (maxLeft->_right)
						{
							pmaxLeft = maxLeft;
							maxLeft = maxLeft->_right;
						}
						cur->_key = maxLeft->_key;
						if (pmaxLeft->_right == maxLeft) //这判断也是一样 如果上面循环没有进去 那么 8这个节点右子树就打乱结构了。
						{
							pmaxLeft->_right = maxLeft->_left;
						}
						else
						{
							pmaxLeft->_left = maxLeft->_left;
						}

						delete maxLeft;

					}
					return true;
				}
			}
			return false;
		}
		Node* Find(const K& key)
		{
			if (_root == nullptr) //如果二叉树为空直接返回假
			{
				return nullptr;
			}
			Node* cur = _root;
			while (cur)//遍历左右子树
			{
				if (cur->_key < key) // 根小于要查找数右子树找
				{
					cur = cur->_right;
				}
				else if (cur->_key > key) // 根大于要查找数左子树找
				{
					cur = cur->_left;
				}
				else    //等于就是找到了 返回真
				{
					return cur;
				}
			}
			return nullptr; //循环结束没找到返回假
		}
		bool Insert(const K& key, const V& value)
		{
			if (_root == nullptr)
			{
				_root = new Node(key,value);
				return true;
			}
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}

			}
			cur = new Node(key,value);
			//链接
			if (parent->_key < key)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}
			return true;
		}
		void InOrder()
		{
			_InOrder(_root);
			cout << endl;
		}
		protected:
			void _InOrder(Node* root)
			{
				if (root == nullptr)
					return;

				_InOrder(root->_left);
				cout << root->_key << ":" << root->_value << endl;
				_InOrder(root->_right);
			}
	private:
		Node* _root = nullptr;

	};
}

在主函数写一个测试函数，看看结果 

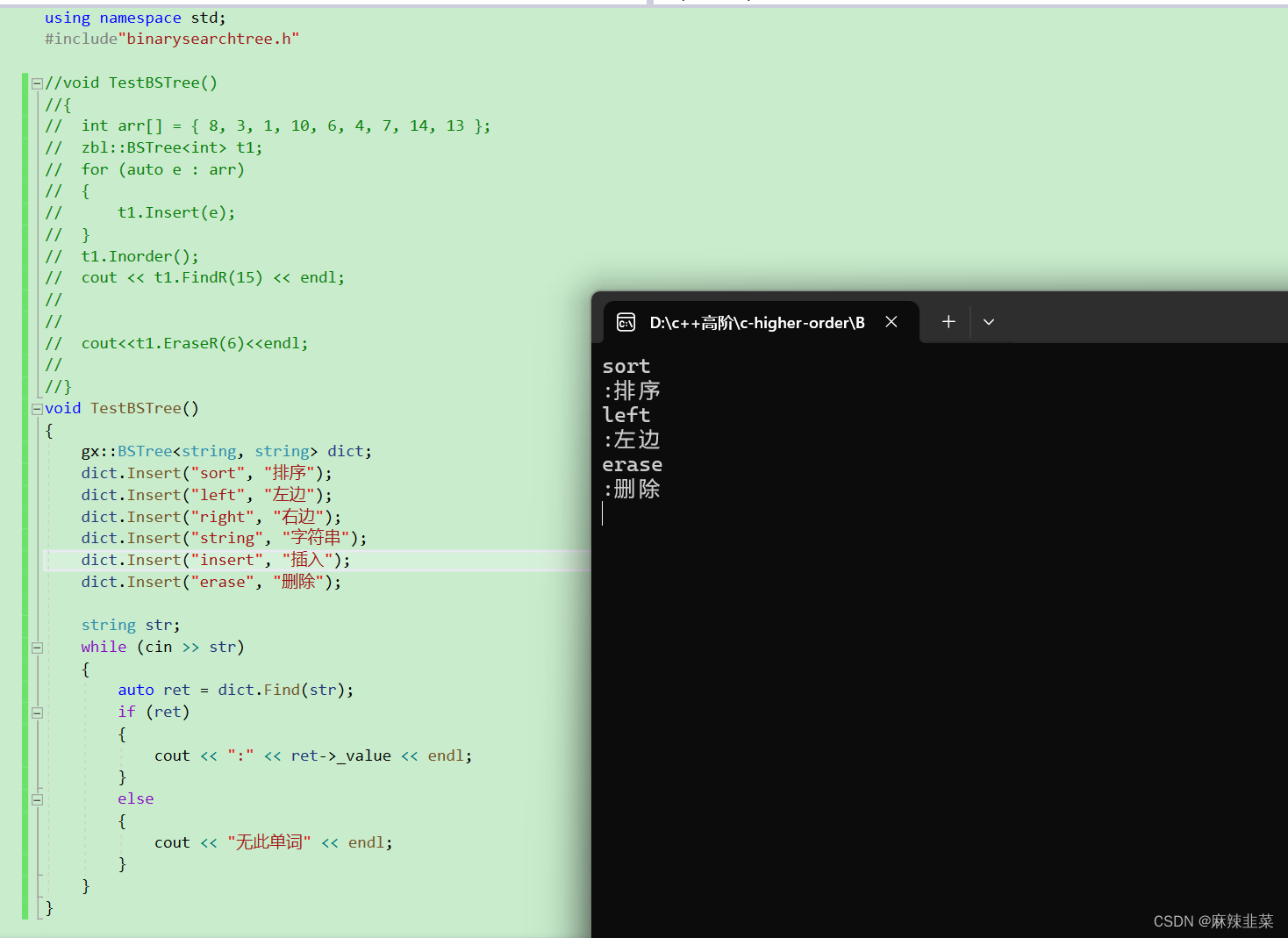
3.二叉搜索树的性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。
对有 n 个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二 叉搜索树的深度的函数，即结点越深，则比较次数越多。
但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜树：
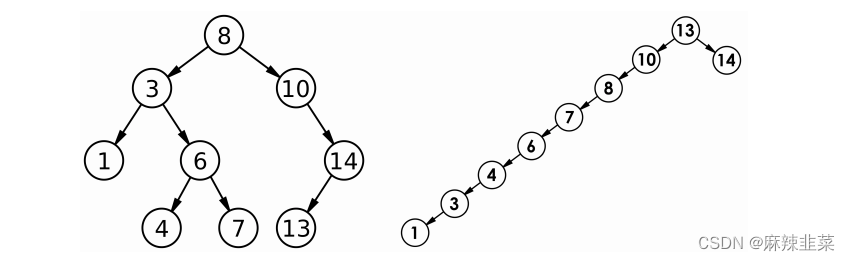
最优情况下，二叉搜索树为完全二叉树 ( 或者接近完全二叉树 ) ，其平均比较次数为： $log_2 N$
最差情况下，二叉搜索树退化为单支树 ( 或者类似单支 ) ，其平均比较次数为： $\frac{N}{2}$
问题：如果退化成单支树，二叉搜索树的性能就失去了。那能否进行改进，不论按照什么次序插
入关键码，二叉搜索树的性能都能达到最优？下篇讲解 AVL 树和红黑树就可以上场了。

麻辣韭菜
关注
  • 10
    点赞
  • 踩
  • 28
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
C++ 二叉搜索树BinarySearchTree
冰果滴的博客
07-30 972
二叉搜索树是为学习map和set做的铺垫，了解了二叉搜索树的特性，有助于更好的理解map和set。
C++ 二叉搜索树
m0_61548909的博客
07-23 575
或者是具有以下性质的二叉树若它的左子树不为空，则左子树上所有节点的值都小于根节点的值若它的右子树不为空，则右子树上所有节点的值都大于根节点的值它的左右子树也分别为二叉搜索树。...
c++ 二叉搜索树
Hedenghui777的博客
06-22 264
在这里为什么我们需要学习二叉搜索树呢？ map和set特性需要先铺垫二叉搜索树，而二叉搜索树也是一种树形结构。 二叉搜索树的特性了解，有助于更好的理解map和set。 1.二叉搜索树 1.1 二叉搜索树概念 二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树: 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值 它的左右子树也分别为二叉搜索树 int a [] = {5,3,4,1,7,8,2,6,0,9}; 1.
【C++】二叉搜索树
qq_62939852的博客
04-18 909
从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。 最多查找高度次，走到到空，还没找到，这个值不存在非空右子树的所有值大于根节点的值 左右子树都是二叉搜索树第一个不满足，因为值为5的节点在值为10的节点的右边，正常来说10的右边都应该比10大分为两种情况 若插入的值在二叉树中不存在，则通过比较进行插入若插入11，因为11比8大，所以跟10比较，而11比10大，所以走10的右子树14，14与11比较，因14>11，所以走14的左子树13，11与13比较，因13>11，故作为13的左子树，遇见NU
C++——二叉搜索树
weixin_49449676的博客
11-30 1875
若要删除8，这里采用右树最左节点的替换法，右树的最左节点就是10自己，如果这样写会有错误，while循环都不会进去，minparent就是空，而后面minParent->_left = min->_right;用左子树的最大节1点或右子树的最小节点4，若采用右树的最小节点，交换3和4删除4之后，删除3，但还有一个子节点5，我们让5成为6的左节点。若果要删除跟节点，而且左为空，若要删除8，我们更新根节点即可，让根节点指向10。若果要删除跟节点，而且右为空，若要删除8，让根节点指向3即可。
c++——二叉搜索树
陌上人如玉，公子世无双。
08-17 311
关联式容器也是用来存储数据的，与序列式容器不同的是，其里面存储的是<key, value>结构的键值对，在数据检索时比序列式容器效率更高。 键值对： 用来表示具有一一对应关系的一种结构，该结构中一般只包含两个成员变量key和value，key代表键值， value表示与key对应的信息。 二叉搜索树： 二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树： ...
C++二叉搜索树——插入
qq_43640822的博客
05-31 464
​ 通过结构体作为节点，结构体包含四个成员，分别是键值key，指向父节点的指针 *parent，指向左子节点的指针 *left，指向右子节点的指针 *right。 struct Node{ int key; Node *left,right,parent; } ​ 从根以起点寻找节点 x 的插入位置。 设当前节点为 x，如果 z 的键值小于 x 则将当前节点的左子节点作为下一个 x，反之则以...
【 C++ 】二叉搜索树
bit_zyx的博客
09-03 918
目录 1、二叉搜索树的概念 2、二叉搜索树的实现 ①、结点类 ②、二叉搜索树的类 2.1、默认成员函数 构造函数 拷贝构造函数 赋值运算符重载函数 析构函数 2.2、中序遍历 2.3、Insert插入函数 ............
C++ 二叉搜索树的应用
m0_72563041的博客
04-20 479
【C++】二叉搜索树的应用场景
C++ 二叉搜索树(BST)的实现方法
08-30
主要介绍了C++ 二叉搜索树(BST)的实现方法，非常不错，具有参考借鉴价值，需要的的朋友参考下
二叉搜索树查找算法【实现】.rar_C++_C++ 二叉搜索树_organizationzme
09-23
C++实现的二叉搜索树的查找算法，查找效率高，速度快，欢迎交流和谈论
C++二叉搜索树的插入和删除例子
05-29
很简单的一个例子！非常适合新手观看！！！！！！！！！！！！！！！！！！！！！
二叉搜索树的c++实现
07-05
使用二叉链表和c++来实现二叉搜索树，提供插入、删除、遍历、求最小节点、最大最节点等操作。
【C++】——Stack与Queue（含优先队列（详细解读）
m0_74092462的博客
06-09 979
优先队列是一种容器适配器，根据严格的弱排序标准，它的第一个元素总是它所包含的元素中最大的。stack是一种容器适配器，专门用在具有后进先出操作的上下文环境中，其删除只能从容器的一端进行元素的插入与提取操作。 队列是一种容器适配器，专门用于在FIFO上下文(先进先出)中操作，其中从容器一端插入元素，另一端提取元素。
C++——计算不同的非空子串个数
我发布的博客，快来抄答案吧
06-09 132
BCSP-X 11题 C++代码详解
LeetCode 算法：轮转数组c++
小金牛来了
06-09 654
LeetCode 算法：轮转数组c++
手搓顺序表（C语言）
最新发布
m0_62646213的博客
06-12 1093
顺序表头插头删，尾插尾删，任意位置插入删除的实现和优劣分析
【2024最新华为OD-C/D卷试题汇总】[支持在线评测] CPU算力分配(100分) - 三语言AC题解(Python/Java/Cpp)
KK爱Coding的博客
06-11 267
### 问题描述 K小姐是某公司运营部门的主管,最近她需要对公司的两组服务器进行算力分配。每组服务器有多个算力不同的 $CPU$,其中 $A$ 组第 $i$ 个 $CPU$ 的运算能力为 $A[i]$,而 $B$ 组第 $i$ 个 $CPU$ 的运算能力为 $B[i]$。一组服务器的总算力是各 $CPU$ 的算力之和。 为了让两组服务器的算力相等,K小姐允许从每组各选出一个 $CPU$ 进行一次交换。她希望从 $A$ 组服务器中选出算力尽可能小的 $CPU$ 来交换,你能帮她计算出应该选择哪两个 $CP
c++二叉搜索树的创建
11-13
以下是C++中创建二叉搜索树的示例代码： ```c++ #include <iostream> using namespace std; // 定义二叉搜索树节点结构体 struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int x) : val(x), left(NULL), right(NULL) {} }; // 插入节点函数 TreeNode* insertNode(TreeNode* root, int val) { if (root == NULL) { return new TreeNode(val); } if (val < root->val) { root->left = insertNode(root->left, val); } else { root->right = insertNode(root->right, val); } return root; } // 创建二叉搜索树函数 TreeNode* createBST(int arr[], int n) { TreeNode* root = NULL; for (int i = 0; i < n; i++) { root = insertNode(root, arr[i]); } return root; } // 中序遍历函数 void inorderTraversal(TreeNode* root) { if (root == NULL) { return; } inorderTraversal(root->left); cout << root->val << " "; inorderTraversal(root->right); } int main() { int arr[] = {5, 3, 7, 1, 4, 6, 8}; int n = sizeof(arr) / sizeof(arr[0]); TreeNode* root = createBST(arr, n); inorderTraversal(root); // 输出：1 3 4 5 6 7 8 return 0; } ```

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值