预测陕西省非私营单位就业人员平均工资

1、原始数据可视化——全国、各地区、各行业

（1）数据

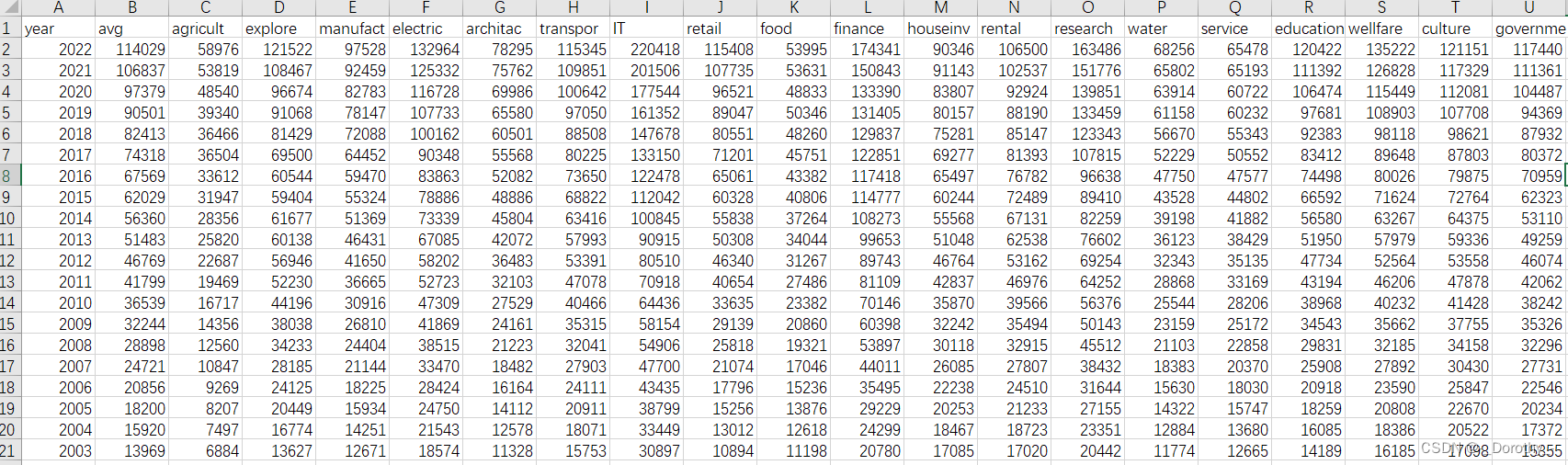
（2）利用arcgis将各个地区的工资可视化在地图上

（3）全国及各个行业地区平均工资的柱状图、箱线图

2、全国平均工资预测——ARIMA预测

（1）原始数据

（2）平稳性检验

ADF检验和差分，一阶差分没有消除趋势性，选择二阶差分效果有很大改善

（3）选参建模

（4）模型评估

残差可视化分析——该模型满足时间序列平稳性、残差独立性、残差正态性，残差同方差性的基本假设

（5）预测

3、地区平均工资预测

（1）ARIMA预测

（a）、原始数据可视化——检查数据趋势、季节性、异常值

（b）、平稳性检验

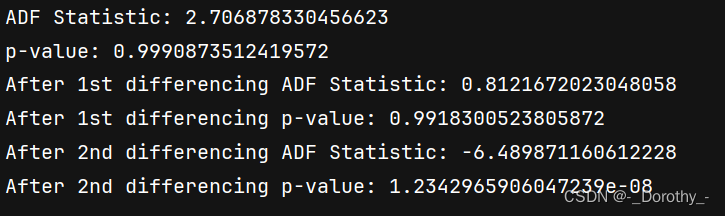
1. 原始数据的ADF检验结果：

   • ADF Statistic: 2.706878330456623
   • p-value: 0.9990873512419572

   这个p值非常高（接近1），表明原始数据序列不是平稳的。我们无法拒绝原假设，即数据存在单位根，数据是非平稳的。

2. 一次差分后的ADF检验结果：

   • ADF Statistic: 0.8121672023048058
   • p-value: 0.9918300523805872

   一次差分后，p值仍然非常高，表示差分后的序列依然是非平稳的。

3. 二次差分后的ADF检验结果：

   • ADF Statistic: -6.489871160612228
   • p-value: 1.2342965906047239e-08

   二次差分后的p值非常低，远小于0.05，这表明我们可以拒绝原假设，即二次差分后的序列是平稳的。

结论：

• 原始数据非平稳：原始数据存在显著的非平稳性。
• 一次差分后仍非平稳：一次差分后的数据依然非平稳。
• 二次差分后达到平稳：二次差分后的数据序列是平稳的。

单次差分结果

一次差分没有去除趋势影响，因此进行二次差分

（c）、确定ARIMA模型参数

图解

自相关和偏自相关——确定AR§、MA(q)阶数

ACF 表示自相关函数，它测量时间序列中每个观测值与之前观测值之间的相关性。如果ACF显示出随着时间间隔的增加而减小，并且最终趋于零，这可能表明时间序列是平稳的。

PACF 表示偏自相关函数，它测量了在控制其他滞后的情况下，两个特定滞后之间的相关性。PACF有助于确定时间序列的滞后阶数。

（d）、预测结果可视化

（e）、模型结果及诊断评估

结果

（f）残差分析

进一步检验残差正态性——Q-Q图

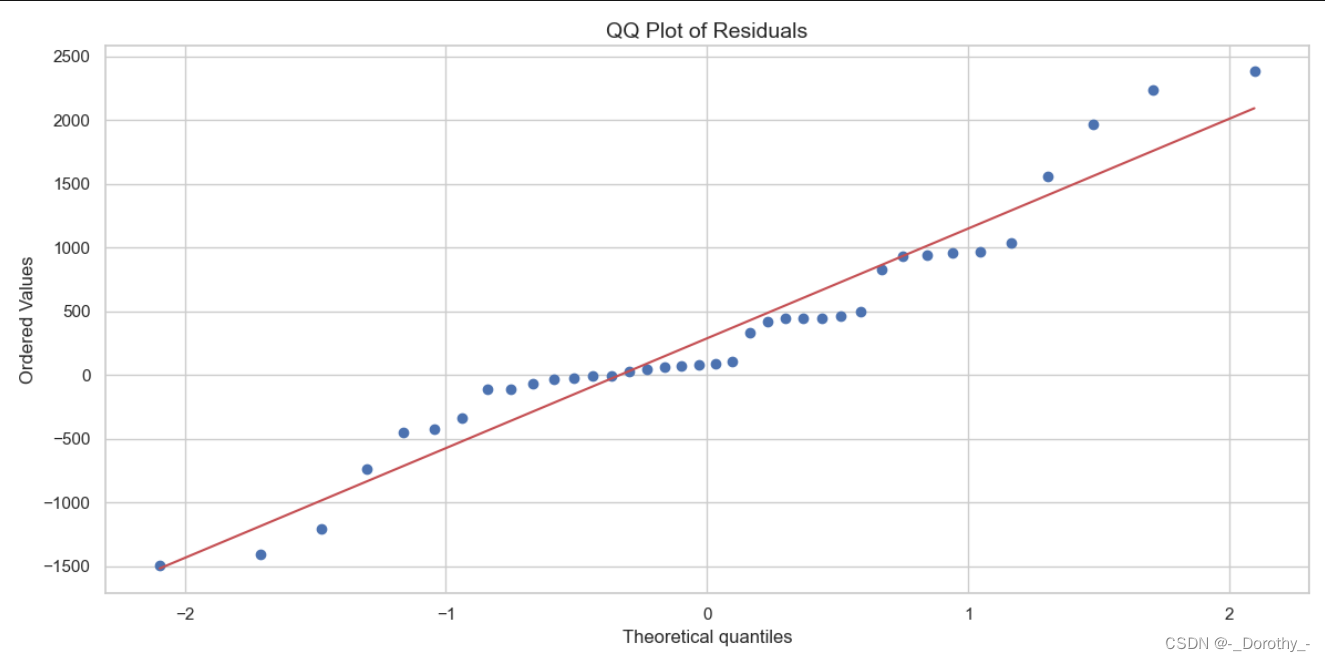
（g）总述

模型系数

1. 截距项（intercept）：
   • 系数：200.5385
   • 标准误差：129.451
   • z值：1.549
   • p值：0.121
   • 95%置信区间：[ -53.181, 454.258]
   • 解释：截距项的p值为0.121，大于常用的显著性水平0.05，表明截距项在统计上不显著。
2. 噪声项方差（sigma2）：
   • 系数：536100.0000
   • 标准误差：97600.000
   • z值：5.495
   • p值：0.000
   • 95%置信区间：[345000.000, 727000.000]
   • 解释：噪声项方差的p值为0.000，小于0.05，表明噪声项方差在统计上显著。

模型总结

• 模型形式：ARIMA(0,2,0)，即这是一个二阶差分的随机游走模型，没有自回归和移动平均项。
• AIC：629.992
• BIC：631.655
• HQIC：630.589
• 对数似然值：-313.996

诊断统计量

• Ljung-Box检验（L1）：
  • Q值：0.48
  • p值：0.49
  • 解释：Ljung-Box检验的p值为0.49，大于0.05，表明残差序列没有显著的自相关性，符合白噪声的假设。
• Jarque-Bera检验（JB）：
  • 统计量：9.53
  • p值：0.01
  • 解释：Jarque-Bera检验的p值为0.01，小于0.05，表明残差序列不符合正态分布假设。
• 异方差性检验（H）：
  • 统计量：14.97
  • p值：0.00
  • 解释：异方差性检验的p值为0.00，小于0.05，表明残差序列存在异方差性。
• 偏度（Skew）：0.82
• 峰度（Kurtosis）：4.78
  • 解释：残差序列的偏度和峰度表明其分布偏离正态分布，具有右偏和尖峰特性。

（h）、结论

1. 模型选择：
   • ARIMA(0,2,0)模型的AIC为629.992，是在所有尝试的模型中最优的。
2. 模型拟合：
   • 模型的截距项在统计上不显著。
   • 残差序列没有显著的自相关性，但不符合正态分布假设且存在异方差性。
3. 诊断与改进：
   • 尽管模型在AIC准则下是最优的，但残差分析表明其分布不符合正态性且存在异方差性。
   • ACF和PACF图的值都趋近于零，表明序列在滞后k后没有明显的自相关或偏自相关结构，这种情况下，可能是一个随机噪声序列，不适合使用ARIMA模型进行建模

（2）指数回归

（a）拟合可视化

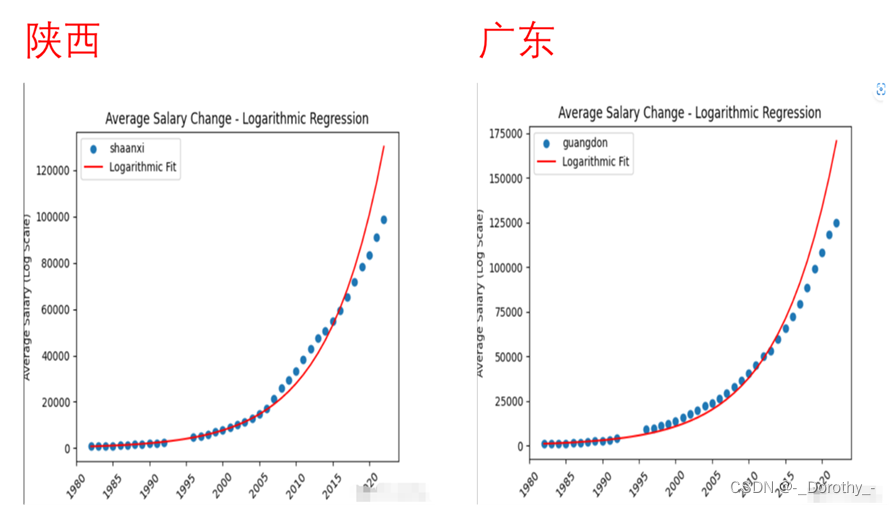
（b）模型诊断

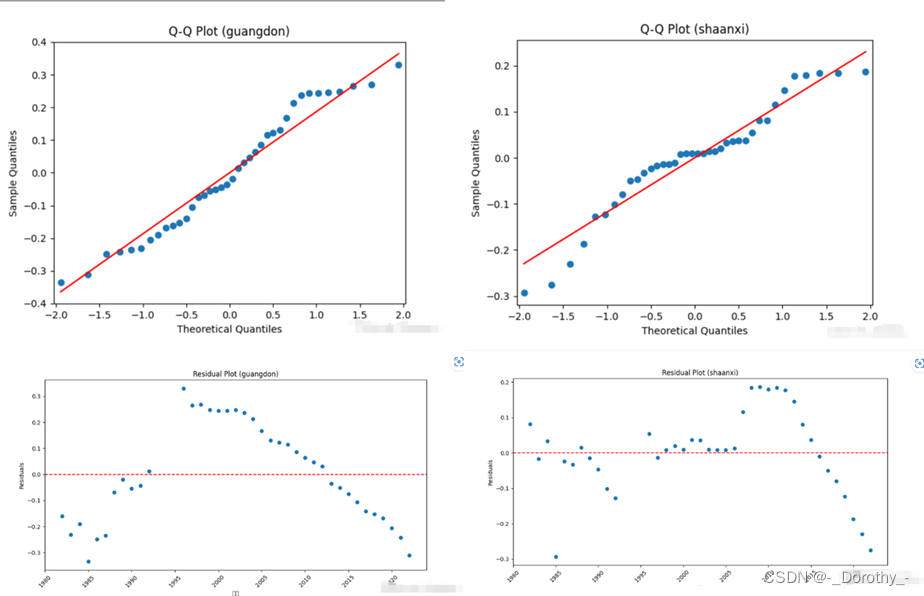
所有地区指数回归可视化结果

（c）预测

（3）多项式回归

（a）拟合可视化

（b）模型诊断

（c）预测

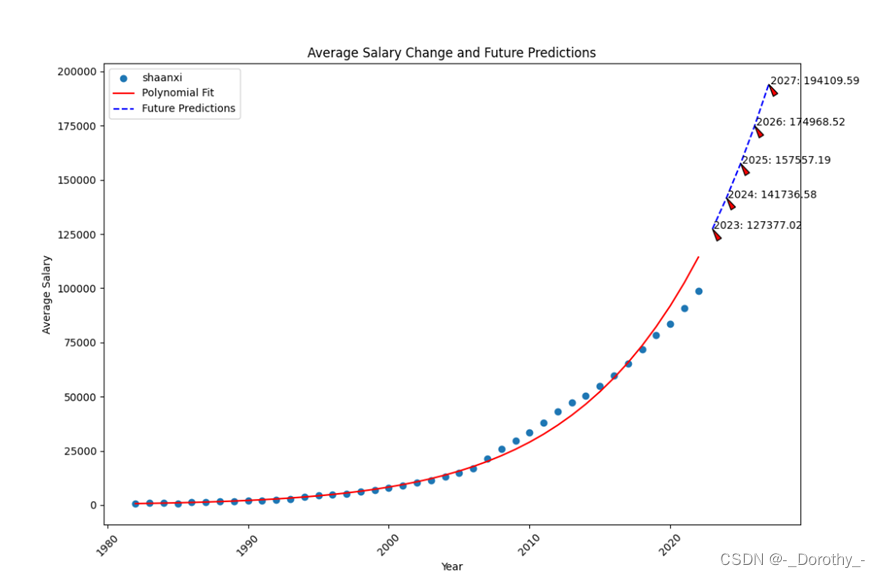
（4）模型诊断评估指标总结