【模板】树状数组 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上 x x x
-
求出某区间每一个数的和
输入格式
第一行包含两个正整数 n , m n,m n,m,分别表示该数列数字的个数和操作的总个数。
第二行包含 n n n 个用空格分隔的整数,其中第 i i i 个数字表示数列第 i i i 项的初始值。
接下来 m m m 行每行包含 3 3 3 个整数,表示一个操作,具体如下:
-
1 x k含义:将第 x x x 个数加上 k k k -
2 x y含义:输出区间 [ x , y ] [x,y] [x,y] 内每个数的和
输出格式
输出包含若干行整数,即为所有操作 2 2 2 的结果。
样例 #1
样例输入 #1
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
样例输出 #1
14
16
提示
【数据范围】
对于
30
%
30\%
30% 的数据,
1
≤
n
≤
8
1 \le n \le 8
1≤n≤8,
1
≤
m
≤
10
1\le m \le 10
1≤m≤10;
对于
70
%
70\%
70% 的数据,
1
≤
n
,
m
≤
1
0
4
1\le n,m \le 10^4
1≤n,m≤104;
对于
100
%
100\%
100% 的数据,
1
≤
n
,
m
≤
5
×
1
0
5
1\le n,m \le 5\times 10^5
1≤n,m≤5×105。
数据保证对于任意时刻, a a a 的任意子区间(包括长度为 1 1 1 和 n n n 的子区间)和均在 [ − 2 31 , 2 31 ) [-2^{31}, 2^{31}) [−231,231) 范围内。
样例说明:
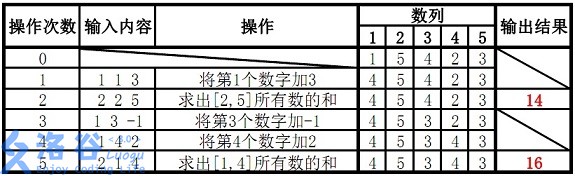
故输出结果14、16
一、引言
在解题过程中,我们有时需要维护一个前缀和数组 S [ i ] = A [ 1 ] + A [ 2 ] + … … + A [ i ] S[i] = A[1]+A[2]+……+A[i] S[i]=A[1]+A[2]+……+A[i] 。但是不难发现,前缀和数组很难快速的支持修改,这里我们引入“树状数组”,他的操作都是 O ( l o g 2 n ) O(log_2{n}) O(log2n) 的,非常高效。
二、基本思想
根据任意整数都可以被转成二进制,若一个数 x x x 的二进制表示为 10101 10101 10101 ,其中等于 1 1 1的位是 0 , 2 , 4 0,2,4 0,2,4 ,则 x x x 可以被“二进制分解”成 2 4 + 2 2 + 2 0 2^4+2^2+2^0 24+22+20 。进一步的,区间 [ 1 , x ] [1,x] [1,x] 可以分成 l o g 2 x log_2x log2x 个小区间:
- 长度为 2 4 2^4 24 的小区间 [ 1 , 2 4 ] [1,2^4] [1,24]。
- 长度为 2 2 2^2 22 的小区间 [ 2 4 + 1 , 2 4 + 2 2 ] [2^4+1,2^4+2^2] [24+1,24+22]。
- 长度为 2 0 2^0 20 的小区间 [ 2 4 + 2 2 + 1 , 2 4 + 2 2 + 2 0 ] [2^4+2^2+1,2^4+2^2+2^0] [24+22+1,24+22+20]
树状数组就是一种基于上述思想的数据结构,其基本用途是维护序列的前缀和,对于区间 [ 1 , x ] [1,x] [1,x] ,将其分为 l o g 2 x log_2x log2x 个子区间,从而快速求得前缀和。
三、基本算法
由上文可知,这些子区间的共同特点是:若区间结尾为 R R R,则区间长度为 R R R 二进制分解下,最小的二的次幂(即从右往左第一个 1 1 1 和后面的 0 0 0 组成的数),我们设为 l o w b i t ( R ) lowbit(R) lowbit(R) 。
此时我们已知右端点和区间长度,可以求得左端点。
设右端点为 r r r,左端点为 l l l, 区间长度为 l e n len len
则有: l e n = r − l + 1 len = r-l+1 len=r−l+1
l e n − 1 = r − l len-1 = r-l len−1=r−l
r − ( l e n − 1 ) = l r-(len-1) = l r−(len−1)=l
r − l e n + 1 = l r-len+1 = l r−len+1=l
l = r − l e n + 1 l = r-len+1 l=r−len+1
将值带入: l = r − l o w b i t ( r ) + 1 l = r-lowbit(r)+1 l=r−lowbit(r)+1
对于给定的数列 A A A,我们建立树状数组 c [ ] c[] c[],其中 c [ x ] c[x] c[x] 保存序列 A A A 的区间 [ x − l o w b i t ( x ) + 1 , x ] [x-lowbit(x)+1,x] [x−lowbit(x)+1,x] 中所有数的和。
树结构如下:
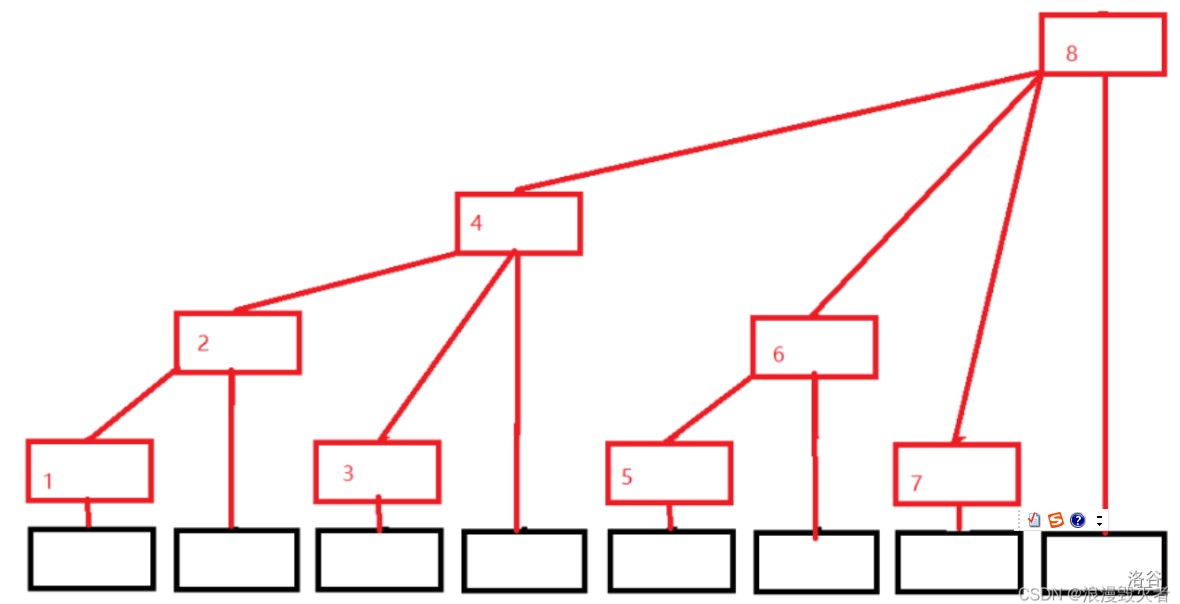
树状数组的深度为 l o g 2 n log_2n log2n,所以一次操作的时间复杂度为 O ( l o g 2 n ) O(log_2{n}) O(log2n)
求 l o w b i t ( i ) lowbit(i) lowbit(i)
l o w b i t ( i ) lowbit(i) lowbit(i) 运算是求 i i i 的二进制分解从右往左第一个 1 1 1 和后面的 0 0 0 组成的数
有: lowbit(i) = (i $ (-i))
其中
$
为按位且运算(两数的二进制每一位,若相同则为
1
1
1 ,不同则为
0
0
0 )
这是为什么呢??
首先了解一下 原码、反码、补码
原码: 再一个二进制数前添加符号位,正数为 0 0 0 , 负数为 1 1 1
反码:正数的反码与原码一致,负数的反码是原码每一位取反(除了符号位)
补码:正数的补码与原码一致,负数的补码是反码 + 1 +1 +1
计算机的所有运算都是基于补码的
其中 − i -i −i 的补码是将原码取反再 + 1 +1 +1,此时原码取反,后面的 0 0 0 都变成了 1 1 1,再 + 1 +1 +1时,后面的 1 1 1 不断进位,直到原本的从右往左第一个 1 1 1 处(此时为 0 0 0 ),停止进位,这时进行与原码按位与运算,由于前面的数被取反了,所以全被抵消了,只留下从右往左第一个 1 1 1 和后面进位后的 0 0 0,于是我们的目的达成了!
有几个例子:

代码实现:
int lowbit(i) { return (i & (-i)); }
建树:
由前面的定义 ( 其中 c [ x ] c[x] c[x] 保存序列 A A A 的区间 [ x − l o w b i t ( x ) + 1 , x ] [x-lowbit(x)+1,x] [x−lowbit(x)+1,x] 中所有数的和 ) 我们可以实现建树,即使用一个普通前缀和数组,进行对树状数组的赋值
求前缀和:
我们要求 [ 1 , x ] [1,x] [1,x] 的和,由于区间 [ 1 , x ] [1,x] [1,x] 可以分成 l o g 2 x log_2x log2x 个小区间,我们要把每个小区间的和统计起来,即可求得 [ 1 , x ] [1,x] [1,x] 的和。
前面已经推导过了,当区间的右端点为
r
r
r 时,左端点为
r
−
l
o
w
b
i
t
(
r
)
+
1
r-lowbit(r)+1
r−lowbit(r)+1 ,
这时,该区间前一个区间的右端点即为
r
−
l
o
w
b
i
t
(
r
)
r-lowbit(r)
r−lowbit(r) ,这样我们就可以处理每个区间了,再进行求和,即可求出前缀和。
代码:
int sum(int x)
{
int ans = 0;
for(int i=x;i>=1;i=i-lowbit(i))
ans += c[i];
return ans;
}
求区间和:
和普通的前缀和类似,直接调用 sum(r)-sum(l-1) 即可。
代码:
int ask(int x, int y) { return sum(y) - sum(x-1); }
单点修改:
前面我们进行求前缀和时,其实是需要到达其子节点进行统计和的,但是我们单点修改却正好相反,需要把其父节点进行更改,前面到达子节点需要 − l o w b i t ( i ) -lowbit(i) −lowbit(i),那么反过来,到达父节点就需要 + l o w b i t ( i ) +lowbit(i) +lowbit(i),不断修改覆盖了该节点的父节点,即可实现单点修改。
代码:
void add(int x, int y)
{
for(int i=x;i<=n;i=i+lowbit(i))
c[i] += y;
}
至此,我们就把基础的树状数组实现了,完整AC代码:
#include<iostream>
using namespace std;
int a[500005], c[500005], s[500005];
int n, m;
int lowbit(int i) { return (i & (-i)); }
int sum(int x)
{
int ans = 0;
for(int i=x;i>=1;i=i-lowbit(i))
ans += c[i];
return ans;
}
int ask(int x, int y) { return sum(y) - sum(x-1); }
void add(int x, int y)
{
for(int i=x;i<=n;i=i+lowbit(i))
c[i] += y;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(0), cout.tie(0); // 加速读入
cin >> n >> m;
for(int i=1;i<=n;i++) { cin >> a[i]; s[i] = s[i-1]+a[i]; }
for(int i=1;i<=n;i++)
{
int l = i-lowbit(i)+1, r = i;
c[i] = s[r]-s[l-1];
}
for(int i=1;i<=m;i++)
{
int op, x, y;
cin >> op >> x >> y;
if(op == 1) add(x, y);
else cout << ask(x, y) << endl;
}
return 0;
}
AC记录

小结:
树状数组代码量少,短小精悍,是处理此类问题的利器,与线段树相比,线段树解决的问题更多样,但是树状数组的常数更小,效率更高,代码量也更少,编程难度更小,以此题为例:
可以看出,同样的题目,树状数组的时间比线段树少了大约 200 m s 200 ms 200ms
注意事项:
由于 l o w b i t ( 0 ) = 0 lowbit(0) = 0 lowbit(0)=0 ,所以树状数组只能处理下标从 1 1 1 开始的数组,从 0 0 0 开始会造成死循环
 树状数组操作详解:区间求和与修改,
树状数组操作详解:区间求和与修改,








 本文详细解释了如何利用树状数组进行区间和计算、单点修改,展示了在给定数列上执行高效操作的方法,适合IT技术学习者理解数据结构应用。
本文详细解释了如何利用树状数组进行区间和计算、单点修改,展示了在给定数列上执行高效操作的方法,适合IT技术学习者理解数据结构应用。
















 413
413

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








