最小生成树问题（附带图的遍历与连通性）

happy egg

已于 2024-07-03 20:08:13 修改

阅读量660

点赞数 6

文章标签：算法

于 2024-05-26 14:11:36 首次发布

本文链接：https://blog.csdn.net/2301_78778685/article/details/139159283

版权

空间数据结构专栏收录该内容

7 篇文章 0 订阅

订阅专栏

五、图的遍历和图的连通性【上课没讲】
1.无向图

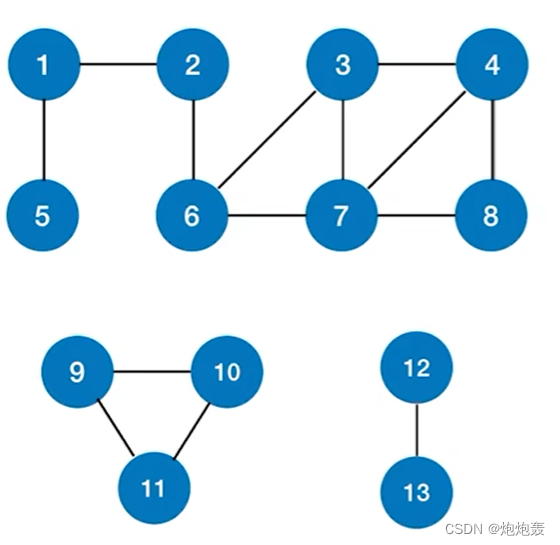
①对无向图进行BFS/DFS遍历，调用BFS/DFS函数的次数=连通分量数；

②对于连通图，只需调用1次BFS/DFS；

2.有向图

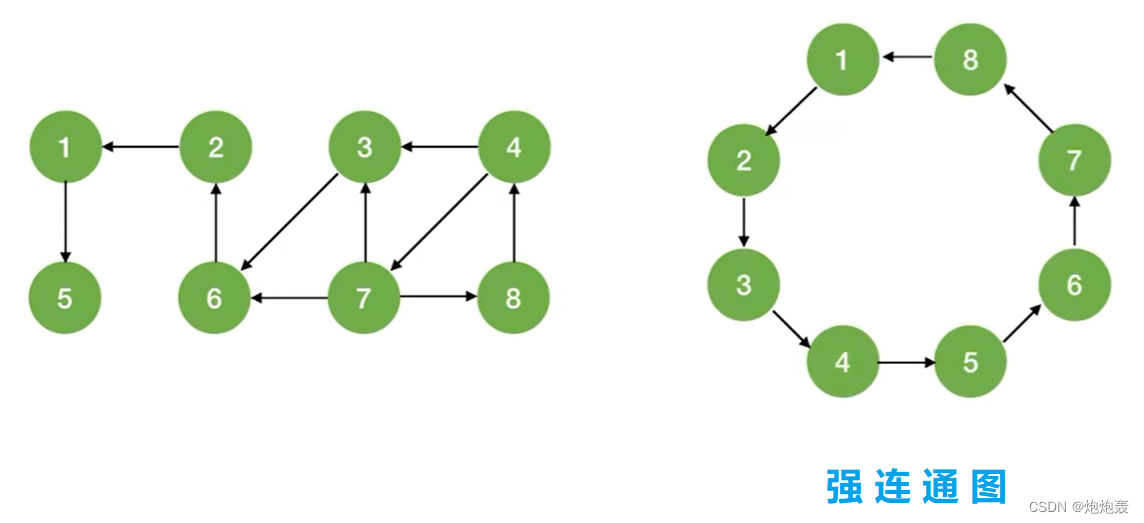
①对有向图进行BFS/DFS遍历，调用BFS/DFS函数的次数要具体问题具体分析；

②若起始顶点到其他各顶点都有路径，则只需调用1次BFS/DFS函数；

③对于强连通图，从任一结点出发都只需要调用1次BFS/DFS。

四、生成树

（一）概述

1. 定义：

所有顶点均由边连接在一起，但不存在回路的图叫生成树

2.分类

（1）对连通图：

分为深度优先生成树和广度优先生成树（仅需调用遍历过程（DFS或BFS）一次，从图中任一顶点出发，便可以遍历图中的各个顶点，产生相应的生成树）

（2）非连通图：

非连通图每个连通分量的生成树一起组成非连通图的生成森林（需多次调用遍历过程）

3.说明：

（1）一个图可以有许多棵不同的生成树

（2）所有生成树具有以下共同特点：

①生成树的顶点个数与图的顶点个数相同

②生成树是图的极小连通子图

③一个有n个顶点的连通图的生成树有n-1条边

④生成树中任意两个顶点间的路径是唯一的

（3）一个连通图的生成树是一个极小的连通子图，它含有图中全部的顶点，但只有足以构成一棵树的n − 1 条边，若砍去它的一条边，则会使生成树变成非连通图；若给它增加一条边，则会形成图中的一条回路。

4. 深度和广度树（辅助理解，不是很重要）

两种方法都是将邻接点作为孩子结点

（1）广度优先遍历生成树

1.每次访问邻接点时，第一次访问的结点作为孩子结点组成的树；

2.广度优先生成树由广度优先遍历过程确定。由于邻接表的表示方式不唯一，因此基于邻接表的广度优先生成树也不唯一；

3.对于非连通图的广度优先遍历，可得到广度优先生成森林。

（2）深度优先生成树

1.图示

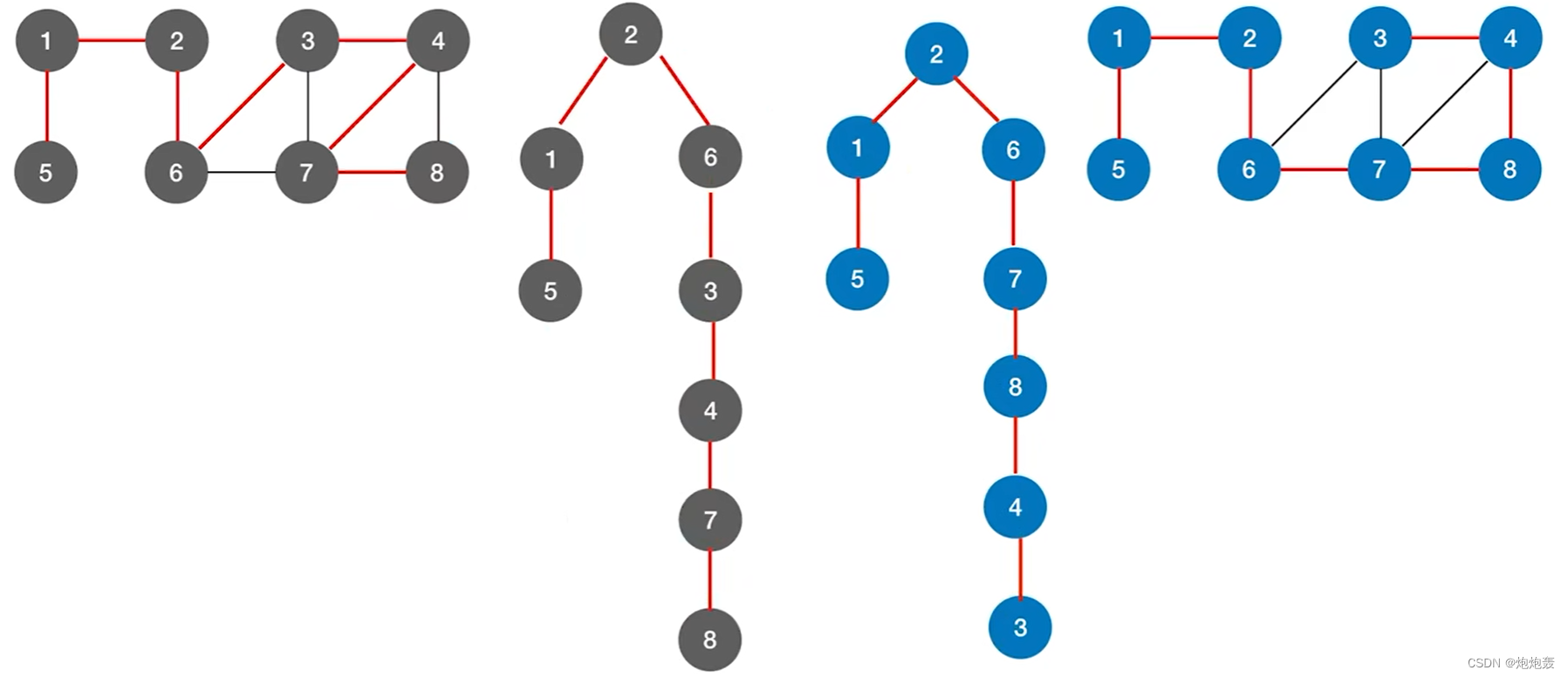
2.唯一性
①同一个图的邻接矩阵表示方式唯一，因此深度优先遍历序列唯一，深度优先生成树也唯一；

②同一个图的邻接表的表示方式不唯一,因此深度优先遍历序列不唯一,深度优先生成树也不唯一；

3.深度优先生成森林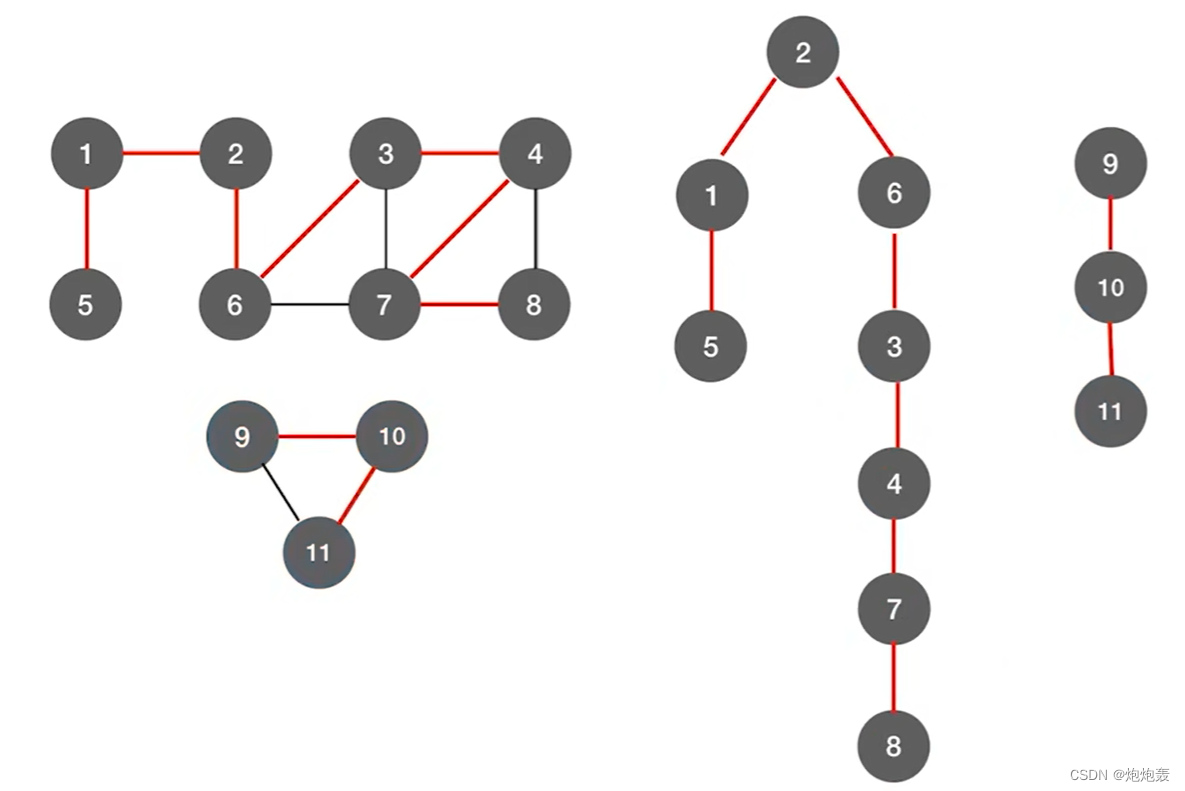

具体需要例子验证，还不是很确定懂了

（二）最小生成树

1. 定义

对于一个带权连通无向图G=(V,E)，生成树不同，每棵树的权也可能不同。其中边的权值之和最小的那棵生成树（构造连通网的最小代价生成树）,称为G的最小生成树(Minimum-Spanning-Tree,MST)

2. 性质

（1）最小生成树可能有多个，但边的权值之和总是唯一且最小的

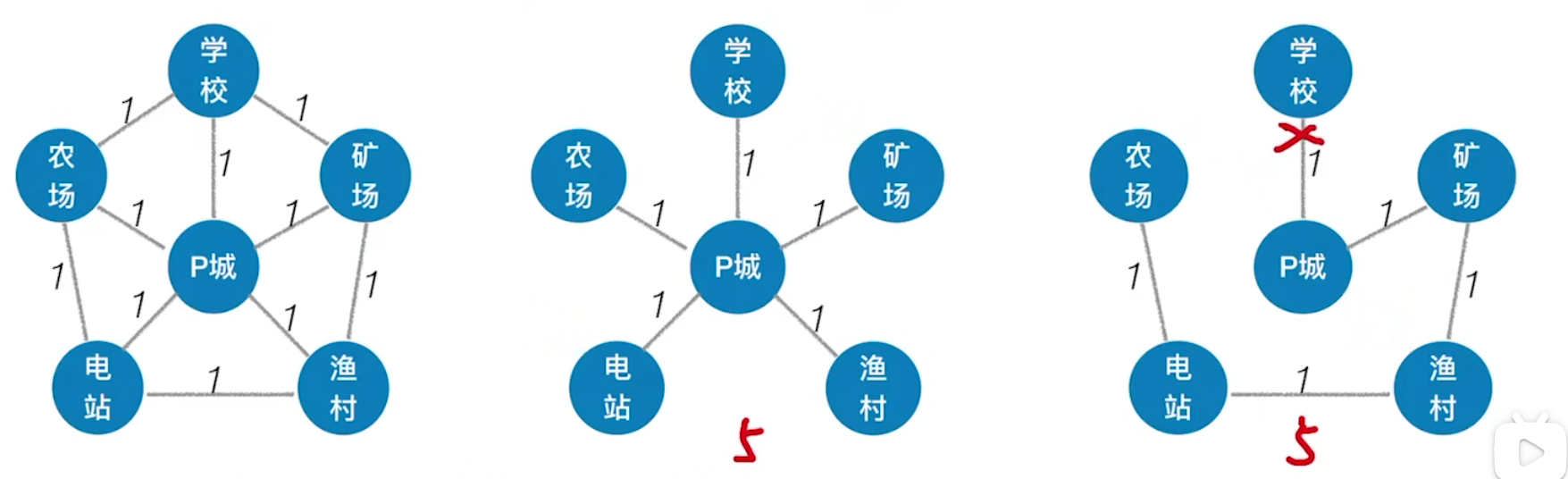
（2）如果一个连通图本身就是一棵树，则其最小生成树就是它本身；

3. 最小生成树算法

6.4_1_最小生成树_哔哩哔哩_bilibili

数据结构：图(Graph)【详解】_图数据结构-CSDN博客

（1）普里姆（Prim）算法

①思路：

将某一个顶点加入树T（此时树中只有一个顶点），之后选择与当前树T中顶点集合相连的边权值最小的顶点，若该新顶点未入树，并将该顶点和对应的边加入树（每次操作后树T中的顶点数和边数都增加1）；若已入树，寻找下一个权值小的顶点。以此类推，直至所有顶点都加入树。（此时T中必然有n-1条边）

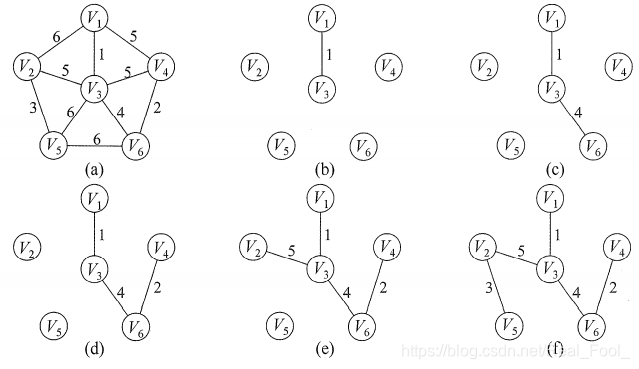
②时间复杂度： $O(|V|^{2})$ 【(n-1)O(n)】，适用于边稠密图（点少边多）；

③算法实现思想

a.图示

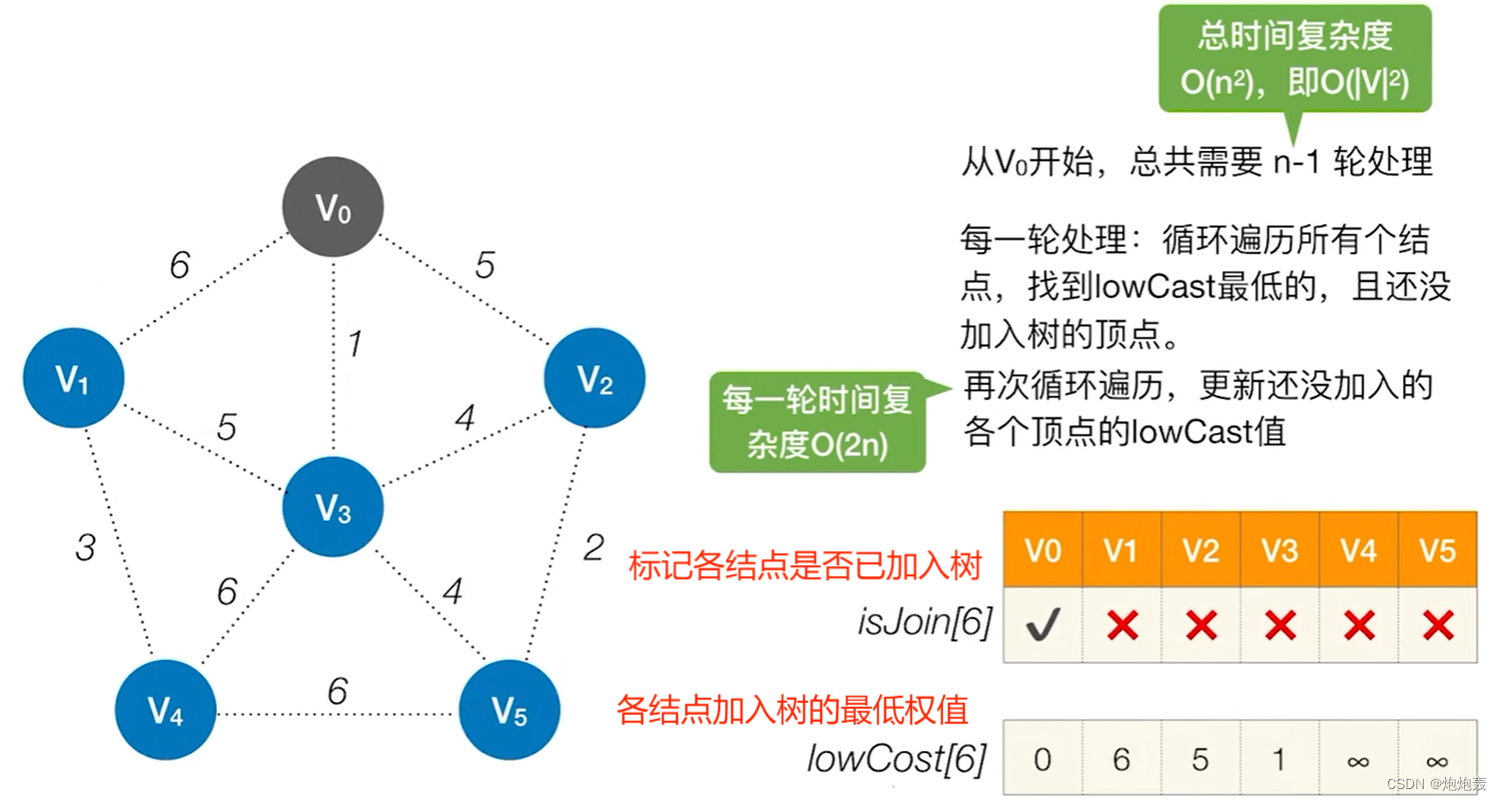
b.步骤

（0）用一个数组记录是否纳入树，用权值数组存放各个顶点加入树的最低权值

（1）初始化时，顶点数组标记域设置为false，选择一个顶点，并标记true；权值数组更新各结点与当前顶点相连的边权值

（2）循环遍历顶点，找到lowcast值最低且未加入的结点，并将这个结点加入树

（3）再次循环遍历，更新还没加入的各个顶点的lowcast值（扫描还没加入树中的顶点，检查未加入的顶点v与新加入的顶点之间是否存在边，若存在，且边的权值比lowcast对应位置的权值更低，就更新lowcast）

（4）重复3、4，直到所有顶点都已经加入树

c.所需数组

需要两个数组，一个存放标记域，一个权值数组存放各个顶点加入树的最低权值

④代码实现

a.邻接矩阵

方法1：

void prim(MGraph G)
{
    //0. 准备工作
	bool isJoin[MaxVerTex];//标记数组
	int lowcost[MaxVerTex];//各结点与当前树顶点集合的最小权值
	int i, j;
	// 初始化标记数组
	for (i = 0; i < G.vexnum; i++)
	{
		isJoin[i] = false;
	}
	//从第一个顶点开始
	isJoin[0] = true;
    
	//初始化权值数组
	for (j = 0; j < G.vexnum; j++)
	{
		lowcost[j] = G.Edge[0][j];
	}

    //1. 循环进行G.vexnum次，即所有顶点都入树
	int k = 0;    //用于记录最低权值的结点序号
	for (int flag = 1; flag < G.vexnum; flag++)
	{
		//2. 循环遍历，找到lowcast值最低且未加入的结点
		int min = INFINITY;
		int before = k;//记录上一个新加入的结点
		for (i = 0; i < G.vexnum; i++)
		{     
            //已加入：isJoin[i]=true （lowcast=0也行，但间接）
			if (!isJoin[i] && lowcost[i] < min)
			{   
				min = lowcost[i];
				k = i;
			}
		}

		//3. 找到权值最小的结点K，入队
		isJoin[k] = true;
		printf("%c->%c,%d\n", G.data[before], G.data[k], min); //打印最小生成树

		//4. 再次循环遍历，更新lowcast值
		lowcost[k] = 0;
		for (i = 0; i < G.vexnum; i++)
		{
			if ((!isJoin[i]) && lowcost[i] > G.Edge[k][i])//把自己的也换了 ，变0
			{
				lowcost[i] = G.Edge[k][i];
			}
		}
	}
}

方法1小结：根据步骤描述即可做出来，两个数组

方法2 ：

void Prim(MGraph g)
{
    int lowcost[MAX_NUM]; // 存储顶点到集合U的最短边权值
    int adjvex[MAX_NUM]; // 存储最短边起点的下标
    for (int i = 1; i < g.vexnum; i++)
    {
        lowcost[i] = g.arc[0][i]; 
        adjvex[i] = 0;
    }
    for (int i = 1; i < g.vexnum; i++)
    {
        int min = INFINITY;
        int k = 0;
        for (int j = 1; j < g.vexnum; j++)
        {
            if (lowcost[j] != 0 && lowcost[j] < min)
            {
                min = lowcost[j];
                k = j; 
            }
        }// 找出剩余顶点中权值最小的边
        printf("%c -> %c : %d\n", g.data[adjvex[k]], g.data[k], min); 
        // 打印最小生成树的边和权值  最短边的起点，即上一个新加入的结点
        lowcost[k] = 0; // 将该顶点加入集合U
        // 更新lowcost和adjvex数组
        for (int j = 1; j < g.vexnum; j++)
        {
            if (lowcost[j] != 0 && g.arc[k][j] < lowcost[j])
            {
                lowcost[j] = g.arc[k][j];
                adjvex[j] = k;
            //如果通过新加入的顶点k可以得到更短的路径，则更新lowcost和adjvex
            }
        }
    }
}

法2小结：

adjvex[]数组用于存放最短边起点的下标：
adjvex[ j ] = k 作用是记录【顶点 j 通过最短边连接到生成树的顶点 k 】，追踪生成树的边和起点终点关系。
当发现从新加入的顶点 k 到顶点 j 的边权值比当前记录的 lowcost[ j ]更小时，表示通过顶点k到定点j的路径是目前最短的。于是，更新lowcost[ j ]为g.arc[k][j]，并将 adjvex[ j ] 更新为k 【新的最短边的起点】

注意：----------------------------------------------------------------------------------------------------------------

读取带权无向图的邻接矩阵时候，边数arcnum计算方法如下【prim.c文件中有完整测试代码】

fscanf(fp, "%d", &m.Edge[i][j]);
if ( m.Edge[i][j] != 0 && m.Edge[i][j] != INFINITY)  //!!!
{
    m.arnum++; //弧数arnum的计算方法
}
//如果是无向图的话，arnum会重复，真实的应该除以2

b.邻接表

to do ..... .

（2）克鲁斯卡尔（Kruskal）算法

①思路：

按照边的权值由小到大的顺序，不断选取当前未被选取过且权值最小的边，若该边依附的顶点所属集合不同（即不连通），则将此边加入树，否则舍弃此边而选择下一条权值最小的边。以此类推，直至T中所有顶点都在属于同一个集合（即连通）上

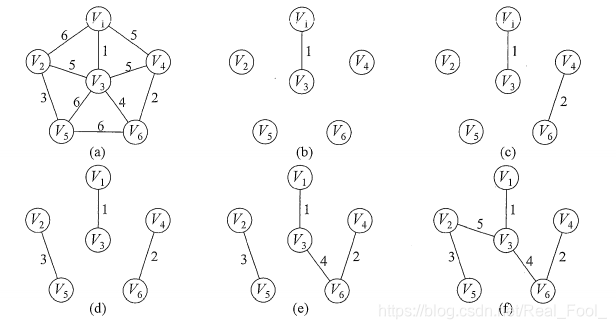
②时间复杂度： $O(|E|log_{2}|E|)$ ，适用于边稀疏图（点多边少）；

③算法实现思想

a.图示

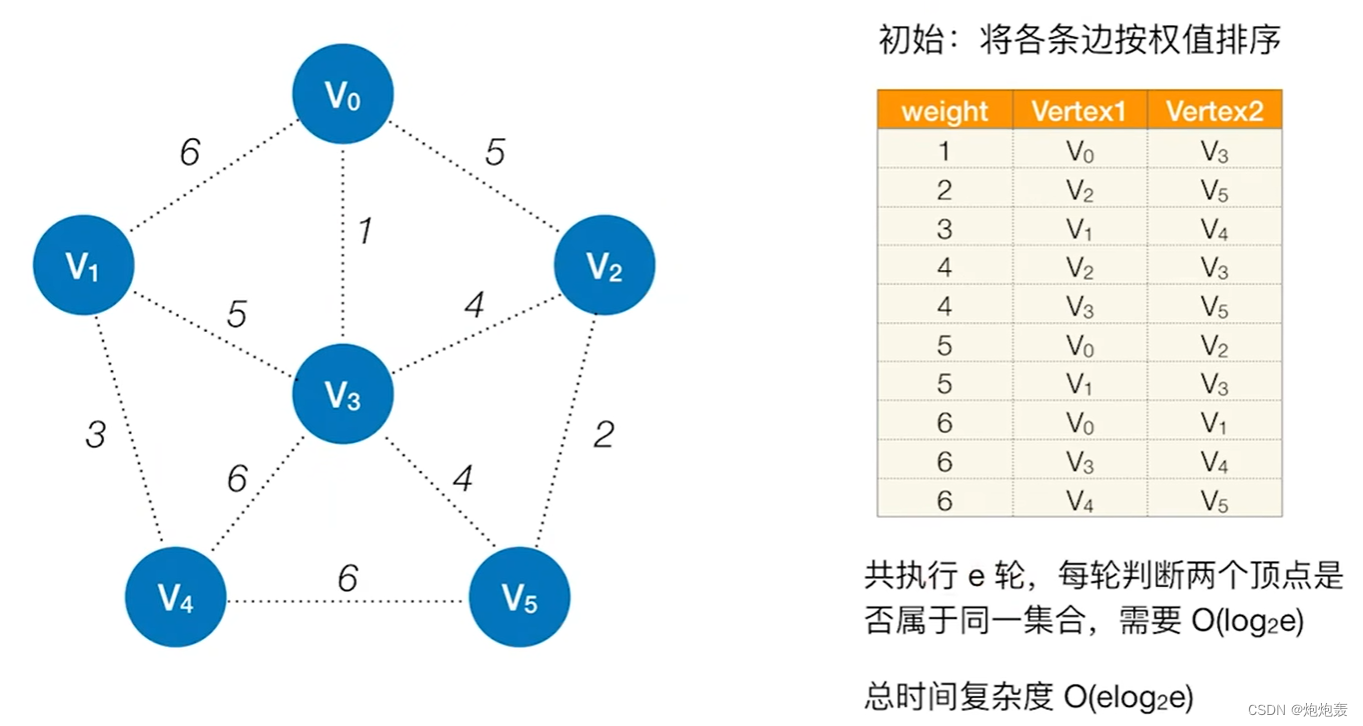
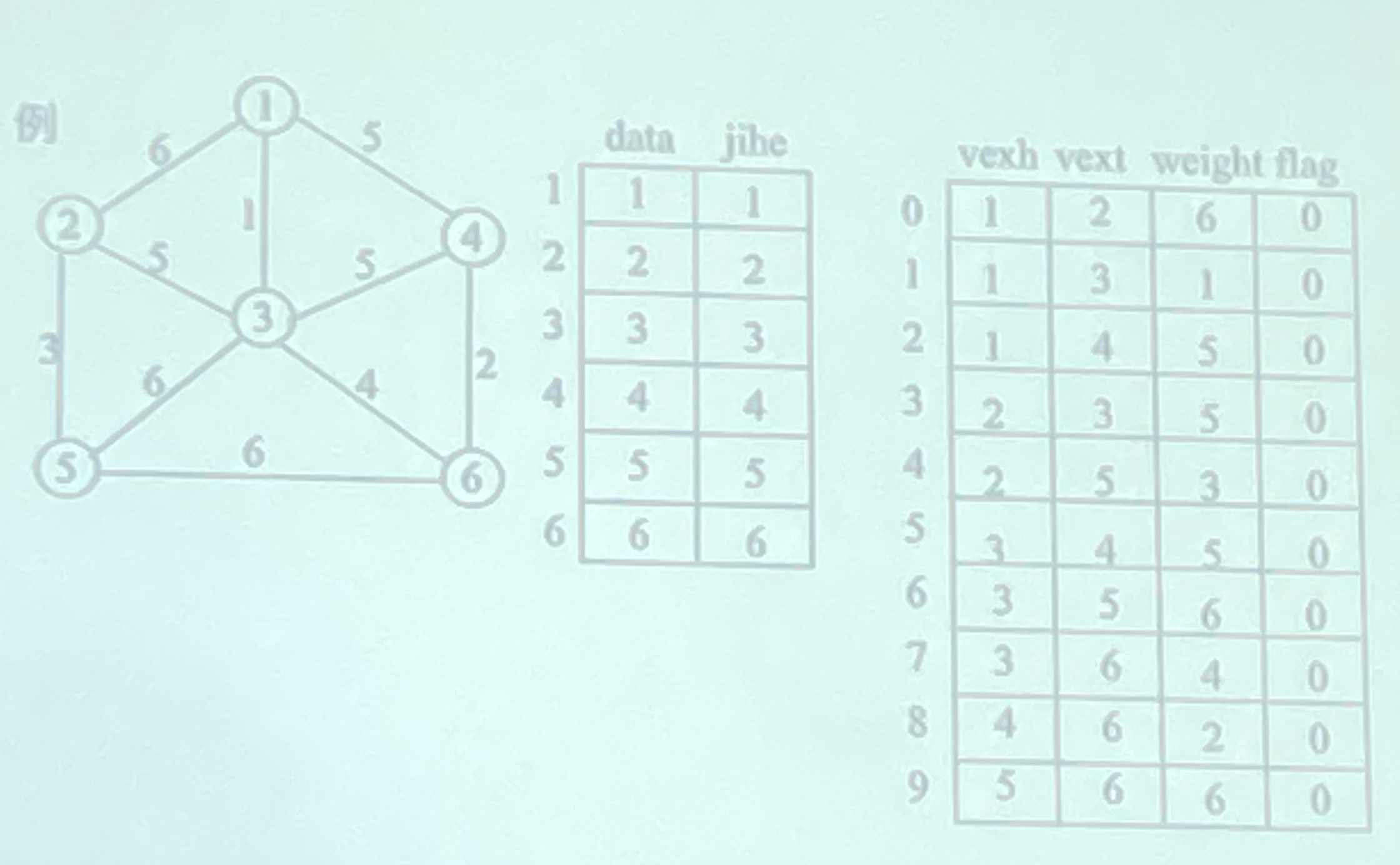
b.步骤

（0）用顶点数组和边数组存放顶点和边信息

（1）初始化时，顶点数组中令每个顶点的jihe互不相同；边数组中令每个边的flag为0，并将边按权值排序

（2）选出权值最小且flag=0的边

（3）若该边依附的两个顶点的jihe值不同，即非连通，则令该边的flag=1，选中该边；再令该边依附的两顶点的jihe以及两集合中所有顶点的jihe相同。若该边依附的两个顶点的jihe值相同，即连通，则令该边的flag=2，即舍去该边

（4）重复上述步骤，直到选出n-1条边位置

c.所需结构体

因此，需要两个定义两个结构体，一个是顶点数组：用于存放顶点信息与所属集（直接用一个数组存储所属集合也行）；一个是边数组，用于存放边的两个顶点、权值、入树标志：

//顶点结点
typedef struct
{
	int data;//顶点信息
	int jihe;//所属集合
}VEX;
//边结点：
typedef struct
{
	int vexh, vext;//边依附的两顶点
	int weight;//边的权值
	int flag;//标志域
}EDGE;

④代码实现

方法1——byself

//边结点：
typedef struct
{
	int vexh, vext;//边依附的两顶点
	int weight;//边的权值
	int flag;//标志域
}EDGE;

void kruskal(MGraph G)
{
	int jihe[MaxVerTex];//各个顶点所属集合数组
	EDGE edge[MaxVerTex];//边数组

	//0. 初始化
	int i=0,j=0,t=0; //t用于记录边数 
	for (i = 0; i < G.vexnum; i++)
	{
		//集合数组
		jihe[i] = i;
		//边数组
			//权值和顶点初始化，遍历邻接矩阵
		for (j = i+1; j < G.vexnum; j++)//避免重复边
		{
			if (G.Edge[i][j] != 0 && G.Edge[i][j] != INFINITY)//记录有效边
			{
				edge[t].vexh = i;
				edge[t].vext = j;
				edge[t].weight = G.Edge[i][j];
				edge[t].flag = 0;//每个边都未入树
				t++;
			}
		}
	}//边数组是否要按权值排序？不排其实也行，每次用循环找最小的
	
	//1. 循环进行n-1次，选出n-1条边，只有选中才+1
	int flag = 0;
	while(flag<G.vexnum-1)
	{
		//2.循环遍历边数组，选出权值最小且未入树的边
		int min = INFINITY;
			//记录权值最小边的两个顶点序号，和边序号
		int r = -1, l = -1, k = -1; // 初始化为无效值
		
		for (j = 0; j < G.arnum; j++)
		{
			if (edge[j].flag == 0 && edge[j].weight<min)
			{
				min = edge[j].weight;
				r = edge[j].vexh;
				l = edge[j].vext;
				k = j;
			}
		}//选出r、l构成的最小权值边k

		//3. 判断两顶点是否属于同一个集合
		if (jihe[r] != jihe[l])
		{
			//3.1 选中该边
			edge[k].flag = 1;
			printf("%c-%c,%d\n", G.data[r], G.data[l], edge[k].weight);
			flag++;  //计数
			//3.2 设置为相同集合      
			for (i = 0; i < G.vexnum; i++)
			{
				if (jihe[i] == jihe[r])//oldset
				{
					jihe[i] = jihe[l];//newset
				}
			}
		}
		else
		{	//如果属于同一个集合，舍弃这条边k
			edge[k].flag = 2;
		}
	}
}

方法2——来自熊猫

很简洁，熊猫就是厉害捏！！！！待学习

void Kruskal(MGraph g)
{
    int parent[MAX_NUM];//用于标记顶点所在集合
    for (int i = 0; i < g.vexnum; i++)
    {
        parent[i] = i;
    }//最初每个顶点分别属于不同集合
    int edgeCount = 0;

    while (edgeCount < g.vexnum - 1)//最小生成树的边数为顶点数减一
    {
        int MIN = INFINITY;
        int row = 0, col = 0;
        for (int i = 0; i < g.vexnum; i++)
        {
            //避免访问重复边的方法 j=i+1
            for (int j = i + 1; j < g.vexnum; j++)//
            {
                if (g.arc[i][j] < MIN && g.arc[i][j] != 0)
                {
                    MIN = g.arc[i][j];
                    row = i;
                    col = j;
                }
            }
        } //1. 遍历邻接矩阵找到权重值最小的边
        if (parent[row] != parent[col])
        {
            printf("%c -> %c : %d\n", g.data[row], g.data[col], MIN);
            for (int i = 0; i < g.vexnum; i++)
            {
                if (parent[i] == parent[col])
                {
                    parent[i] = parent[row];
                }
            }// 2. 合并顶点集
            edgeCount++;
        }
        g.arc[row][col] = g.arc[col][row] = 0;  // 3. 标记已加入最小生成树
    }
}

小结：

1. 如何合并集合：遍历集合数组，将所有与 r 顶点相同集合的设置为 l 顶点的结合

for (i = 0; i < G.vexnum; i++)
{
    if (jihe[i] == jihe[r])//oldset
    {
        jihe[i] = jihe[l];//newset
    }
}

2. 如何避免重复的边：在访问邻接矩阵时，j 从i+1开始遍历！！！

3. 为什么标记域分为0 1 2，因为分为：未加入的边、加入的边、舍弃的边；而prim只分为：加入的顶点、未加入的顶点

4. ①kruskal算法主循环要进行n-1次（找到n-1条边），不能使用for循环，因为使用for循环的话，不管第一次选择的边是否入树（比如选中边顶点属于同集合，flag=2），循环次数都会+1。

②而prim算法两种循环方式都能使用，这是因为：

prim只需要选择【权值最小且未加入树的顶点】，这种情况下每次循环都是可以找到符合条件的顶点的。
而kursal 【选择权值最小且未入树的边】之后，还需要【判断两顶点是否属于同一集合】。前者每次都能找到，但是后者却不一定都符合条件，因此不一定每次循环都能成功选入一条边。

5.法1中，根据邻接矩阵初始化边数组的时候，边数组edge[ ]的索引不应该是 i ，（这样会导致每个顶点只记录最后一条边，前面的都被覆盖）；正确的做法是边数组edge[ ]应该使用独立的索引 K 来记录图所有的边（这样记录一条边,K++，图有多少条边，K最终就等于多少）

for (i = 0; i < G.vexnum; i++) {
    for (j = i + 1; j < G.vexnum; j++) { // 避免重复边
        if (G.Edge[i][j] != 0 && G.Edge[i][j] != INFINITY) { // 记录有效边
            edge[i].vexh = i;
            edge[i].vext = j;
            edge[i].weight = G.Edge[i][j];
            edge[i].flag = 0; // 每个边都未入树
        }
    }
}

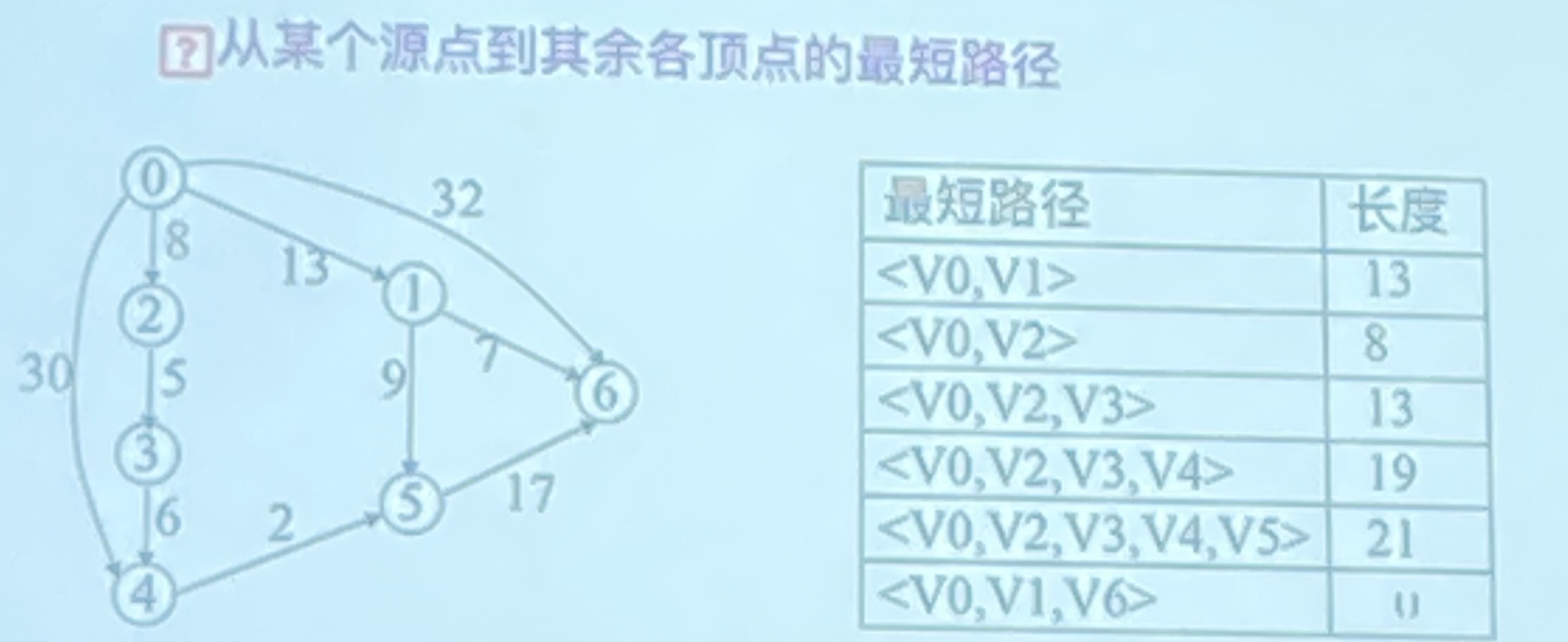
（三）最短路径

1 .定义

用带权有向图表示一个交通运输网，图中：顶点——表示城市；边——表示城市间的交通联系；权——表示此线路的长度或沿此线路运输所花的时间或费用等

最短路径：从某顶点出发，沿图的边到达另一顶点所经过的路径中，边权值之和最小的一条路径

2.迪杰斯特拉（Dijkstra）算法

6.4_3_最短路径问题_Dijkstra算法_哔哩哔哩_bilibili

（1）算法概述

Dijkstra算法用于构建单源点的最短路径，即图中某个点到任何其他点的距离都是最短的。例如，构建地图应用时查找自己的坐标离某个地标的最短距离。
它并不是一下子求出了V0到V8的最短路径，而是一步步求出它们之间顶点的最短路径，过程中都是基于已经求出的最短路径的基础上，求得更远顶点的最短路径，最终得到你要的结果
为解决BFS算法局限于不带权图的情况，对于带权有向图的最短路径，采用Dijkstra算法.

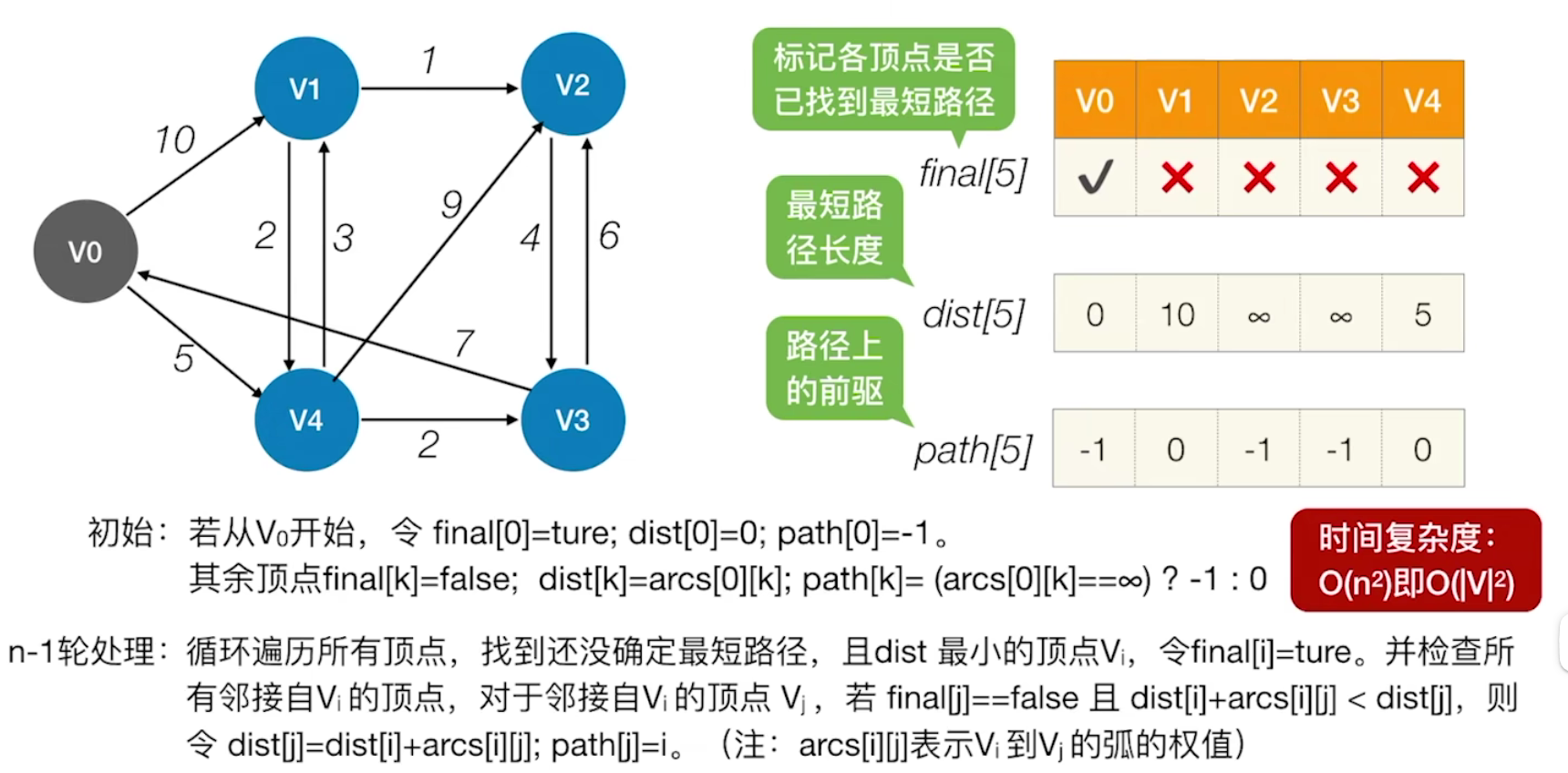
（2）算法实现思想/步骤

①选择一个起点，并初始化三个数组

final[ ]标记各顶点是否已找到最短路径。因为V0到V0的路径为0，也就意味着我们已经找到V0的最短路径，所以将final[0]标记为true；
dist [ ]标记最短路径长度，若能够找到一个暂时的最短路径长度，就标记为该长度，否则标记为∞；
path[ ] 标记为路径上的该结点的直接前驱，初始化均为-1，V0没有直接前驱，就设为-1即可。

②进行n-1轮处理，得到V0到其他所有顶点的最小路径

循环遍历所有结点，找到还没有确定最短路径、且dis最小的顶点Vi，令final[i]=true【找到】
检查所有与Vi邻接的顶点Vt，若其final值为false，且由Vi出发到Vt的路径更短，则更新dist和path信息

（3）完整实现过程（表格）

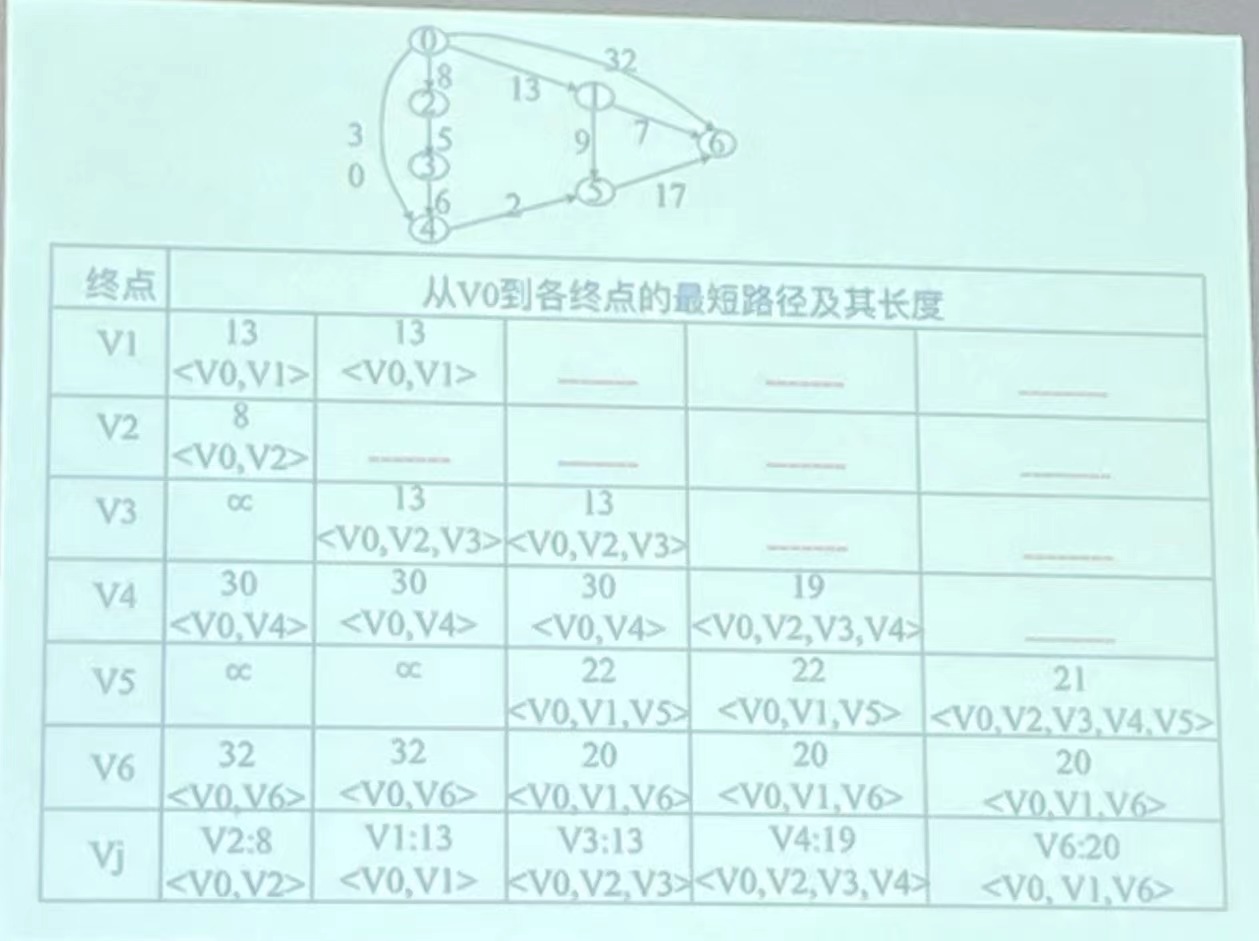
（4）代码实现

void dijkstra(MGraph G)
{
	bool final[MaxVertex];//标记各顶点是否已找到最短路径
	int dist[MaxVertex];//标记从起点到各结点的最短路径长度
	int pre[MaxVertex];//路径上各结点的直接前驱
	int i, j;

	//1. 初始化
		//选择一个起点  可以在函数的变量那里设置start
	printf("起点：%c\n", G.data[0]);
	final[0] = true;
	dist[0] = 0;
	pre[0] = -1;//起点在路径上没有直接前驱
	for (i = 1; i < G.vexnum; i++)
	{
		final[i] = false;
		dist[i] = G.Edge[0][i];
		if (G.Edge[0][i] != INFINITY) //若起点0与顶点i之间有边
		{
			pre[i] = 0;
		}
		else
		{
			pre[i] = -1;
		}
	}
	//2. 进行n-1轮处理，得到V0到其他所有顶点的最小路径
	for (i = 0; i < G.vexnum - 1; i++)
	{
		//3.找到当前最短的路径节点
		int min = INFINITY;
		int t = -1;//记录最新顶点的序号
		for (j = 0; j < G.vexnum; j++)//遍历dist
		{
			if (dist[j] < min  && !final[j])
			{	//权值最小、未找到最短路径
				min = dist[j];
				t = j;
			}
		}//找到了新顶点t 
		final[t] = true;
		printf("%c->%c,%d\n", G.data[pre[t]], G.data[t], dist[t]);
		//3.检查所有与t邻接的顶点，遍历邻接矩阵
		for (int k = 0; k < G.vexnum; k++)
		{
			if (!final[k] && G.Edge[t][k] != INFINITY)//顶点t与顶点k之间有边
			{//存在邻接点k
				int newdist = dist[t] + G.Edge[t][k];
				if (newdist<dist[k]) 
				{//结点k未纳入最短路径，且距离更短
					//更新dist和pre
					dist[k] = newdist;
					pre[k] = t;
				}
			}
		}
	}


	// 输出最终的最短路径和距离
	printf("最终的最短路径和距离：\n");
	for (i = 1; i < G.vexnum; i++)
	{
		printf("%c->%c的路径长度为%d,", G.data[0], G.data[i], dist[i]);
		printf("具体路径为:%c",G.data[i]);
		j = i;
		while (pre[j] != -1)
		{
			printf("<-%c", G.data[pre[j]]);//前驱
			j = pre[j];
		}
		printf("\n");
	}
	
	
}

（5）时间复杂度

每一轮要遍历 $n$ 个顶点选择最小的顶点 i ，又要继续遍历 i 的邻接点，如果是邻接矩阵的话也需要遍历 $n$ 个顶点，因此每一轮时间复杂度为O(n)+O(n)，又因为常数项可以舍弃，每一轮时间复杂度为 $O(n)$ 由于进行 $n-1$ 轮，因此全部时间复杂度为 $O(n^{2})$
如果用邻接表的话，遍历i的邻接点时不需要遍历n个，但是每一轮时间复杂度的量级依然是 $O(n)$

3. 弗洛伊德（Floyd）算法

6.4_4_最短路径问题_Floyd算法_哔哩哔哩_bilibili 了解即可，不需要掌握代码！！

每一对顶点之间的最短路径：
方法1：每次以一个顶点为源点，重复执行Dijkstra算法n次—— $T(n)=O(n^{3})$
方法2：弗洛伊德算法

（1）算法图示（算法思想）：

动态规划思想，将问题的求解分为多个阶段；对于n个顶点的图G，求任意一对顶点Vi->Vj之间的最短路径可分为如下几个阶段：

#初始：不允许在其他顶点中转，最短路径是？

#0：若允许在V0中转，最短路径是？

#1：若允许在V0、V1中转，最短路径是？

#2：若允许在V0、V1、V2中转，最短路径是？

......

#3：若允许在V0、V1、V2......Vn-1中转，最短路径是？

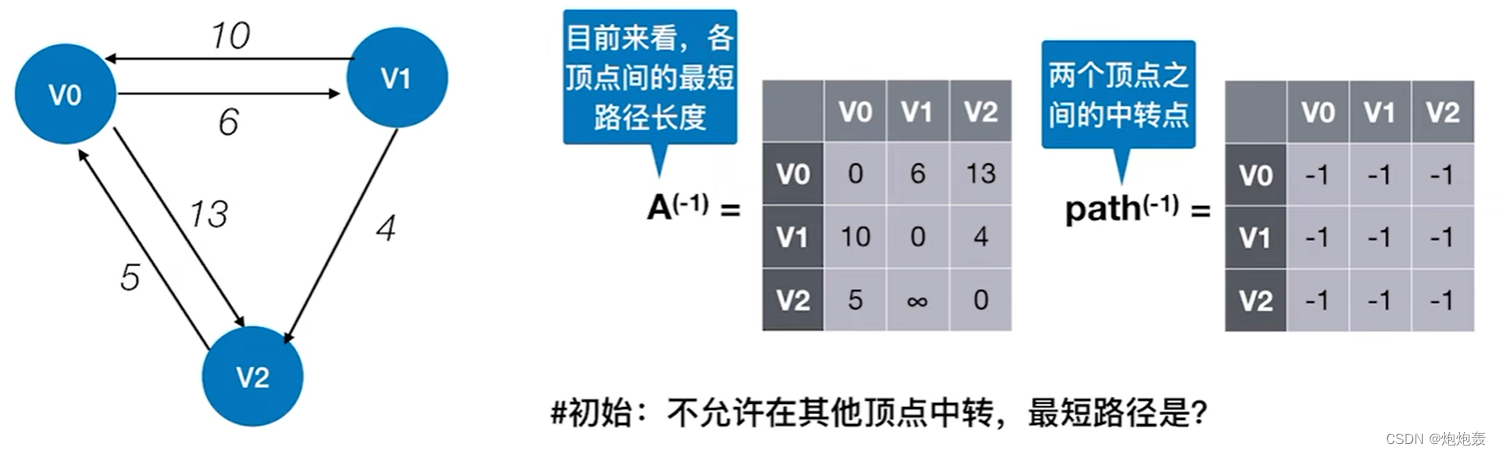
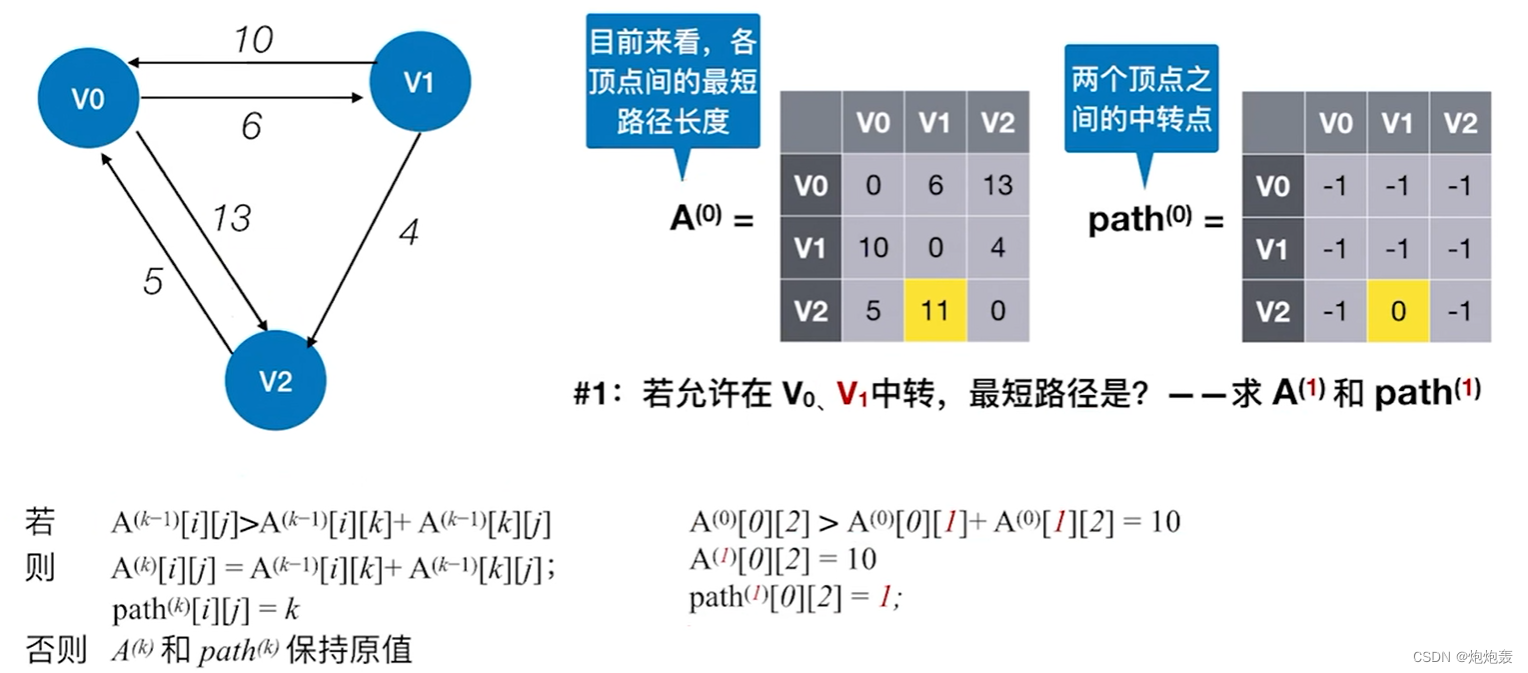
（2）算法步骤：

0. 需要两个二维数组，dist[ ][ ]用于记录当前各顶点间的最短路径长度，path[ ][ ]记录两个顶点之间的中转点

1. 初始化：dist[ ][ ]复制于图的邻接矩阵，值为无穷大即表示两节点间没有边；path[ ][ ]的每个值都设置为-1，表示每个顶点间不存在中转点。

2. 进行n次循环，每次循环以一个结点作为中转点；遍历dist[ ][ ]数组，尝试缩短dist[ ][ ]中的路径长度

3. 在遍历过程中，对任意两个结点 i 和 j ,如果通过节点 k 可以使得 i 到 j 的路径长度更短，即dist [i] [j]<dist i][k]+dist[k] [j]，则更新dist[i] [j]的值为dist[i] [k]+dist[k] [j],path[i] [j]=k

4.当进行n次循环，测试完每个结点作为中转点的结果后，此时dist数组中的值即为图中任意两结点之间的最短路径长度。

（3）代码实现：

//......准备工作,根据图的信息初始化矩阵A和path
for (int k = 0; k < n; k++)						//考虑以Vk作为中转点
{
	for (int i = 0; i < n; i++)					//遍历整个矩阵，i为行号，j为列号
	{
		for (int j = 0; j < n; j++)
		{
			if (A[i][j] > A[i][k] + A[k][j])	//以Vk为中转点的路径更短
			{
				A[i][j] = A[i][k] + A[k][j];	//更新最短路径长度
				path[i][j] = k;					//中转点
			}
		}
	}
}

happy egg

关注

6
点赞
踩
17

收藏

觉得还不错? 一键收藏
0
评论
最小生成树问题（附带图的遍历与连通性）

所有顶点均由边连接在一起，但不存在回路的图叫生成树对于一个带权连通无向图G=(V,E)，生成树不同，每棵树的权也可能不同。其中边的权值之和最小的那棵生成树（构造连通网的最小代价生成树）,称为G的最小生成树(Minimum-Spanning-Tree,MST)用带权有向图表示一个交通运输网，图中：顶点——表示城市；边——表示城市间的交通联系；权——表示此线路的长度或沿此线路运输所花的时间或费用等从某顶点出发，沿图的边到达另一顶点所经过的路径中，边权值之和最小的一条路径Dijkstra算法用于构建。
复制链接

扫一扫

专栏目录