时间复杂度和空间复杂度

时间复杂度和空间复杂度的概念

衡量一个算法的好坏，要从时间和空间两个维度来衡量，时间复杂度主要衡量一个算法运行的快慢，空间复杂度衡量一个算法运行所需要的额外空间，在现在，空间复杂度显得没那么重要，所以我们接下来主要来理解时间复杂度。

时间复杂度

算法的时间复杂度是一个函数，他定量的描述了一个算法执行的时间，但由于数据量不同，环境不同，配置不同，从理论上来说是不能算出来的，但我们可以知道，一个算法执行的时间与执行的次数成正比例，所以，一个算法基本执行的次数，就是时间复杂度。

引例

void func(int n)
{
	int cnt = 0;
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			cnt++;
		}
	}
	for (int i = 0; i < 2 * n; i++)
	{
		cnt++;
	}
	int M = 10;
	while (M--)
	{
		cnt--;
	}
	printf("%d\n", cnt);
}

上图的算法时间复杂度为nn+2n+10，但实际上我们不会用这个函数去表示时间复杂度，我们只会去看时间复杂度的级别，所以我们经常只会保留对这个函数式影响最大的那个数量级，也就是n*n，这就是大O渐进表示法。

大O渐进表示法：

1.用1表示运行时间中所有加法常数。
2.在修改后的运行次数函数中，只保留最高阶项。
3.如果最高阶存在且不是1，则去除与这个项相乘的常数，得到的结果就是大O阶

例1

void func(int m, int n)
{
	int cnt = 0;
	for (int i = 0; i < m; i++)
	{
		cnt++;
	}
	for (int j = 0; j < n; j++)
	{
		cnt++;
	}
}

上图我们用大O渐进表示法可以知道这个时间复杂度为O(m+n),但m和n是没有建立关系的，除非有给出关系n远大于m或者m远大于n，否则无法消去任何一项。

例2

void func()
{
	int cnt = 0;
	for (int i = 0; i < 100000; i++)
	{
		cnt++;
	}
}

上图的时间复杂度为O(1),因为这个算法执行次数是常数次，不管是100，1000，还是100000次的时间复杂度都是O（1）。

例3

计算strchr的时间复杂度：

const char* strchr(const char* str, int character)
{
	while(*str)
	{
		if(*str==character)
			return str;
		else
			++str;
	}
}

上图的时间复杂度为O(n)。
有些算法的时间复杂度存在最好，最坏和平均的情况：
最好情况：任意输入的最小运行次数
最坏情况：任意输入的最大运行次数
平均情况：任意输入的期望运行情况
eg.在一个长度为n的数组里进行查找
最好：1次 最坏：n次 平均：n/2次
实际情况中一般关注算法的最坏情况，所以数组中搜索数据的时间为O(n)。

例4

int Search(int* arr, int n, int x)
{
	assert(arr);
	int left = 0, right = n - 1;
	while (left <= right)
	{
		int mid = left + (right - left) / 2;
		if (arr[mid] > x)
		{
			right = mid-1;
		}
		else if (arr[mid] < x)
		{
			left = mid+1;
		}
		else
		{
			return mid;
		}
	}
}

上图的时间复杂度为O(log n)

例5

long long func(int n)
{
	if (0 == n)
		return 1;
	else
		return func(n - 1)*n;
}

上述算法的时间复杂度为O(n)

long long func(int n)
{
	if (0 == n)
		return 1;
	int cnt=0;
	for(int i=0;i<n;i++)
	{
		cnt++;
	}
	else
		return func(n - 1)*n;
}

上述代码的时间复杂度为O(n^2)

例6

int func(int n)
{
	if(n<3)
		return 1;
	return func(n-1)+func(n-2);
}

上述代码的时间复杂度是2^n，可以画二叉树来理解。

根据上图我们可以看出斐波那契数列算法的递归运行数量呈2的指数倍级别增长。

空间复杂度

空间复杂度是一个数学表达式，是对一个算法运行过程中临时占用的储存空间大小的量度，算多少字节的空间是没有意义的，空间复杂度算的是变量的个数，也用大O渐进表示法表示，函数所需要的栈空间在编译的时候就已经确认好了，因此空间复杂度主要通过函数在运行过程中的额外空间确定。

引例

void bubblesort(int* arr, int n)
{
	for (int i = n; i > 0; i--)
	{
		int ex = 0;
		for (int j = 1; j < i; j++)
		{
			if (arr[j - 1] > arr[j])
			{
				//swap(arr[j - 1], arr[j]);
				int tmp = arr[j - 1];
				arr[j - 1] = arr[j];
				arr[j] = tmp;
				ex = 1;
			}
		}
		if (ex == 0)
			break;
	}
}

上图代码的空间复杂度为O(1)，因为arr是本身必须有的空间，而不是为了排序而临时开的空间，所以在算空间复杂度的时候不能将其计算在内，而像i，j这种变量是常数个，所以空间复杂度为O(1)。

例1

long long* func(size_t n)
{
	if (n == 0)
		return NULL;
	long long* fib = (long long*)malloc((n + 1) * sizeof(long long));
	fib[0] = 0;
	fib[1] = 1;
	for (int i = 0; i <= n; i++)
	{
		fib[i] = fib[i - 1] + fib[i - 2];
	}
	return fib;
}

上图代码的空间复杂度为O(n)。

例2

long long Fib(size_t n)
{
	if(n < 3)
		return 1;
	return Fib(n-1)+Fib(n-2);
}

上图代码的空间复杂度是O(n)，在这里我们要考虑到递归调用的栈帧的消耗，比如说Fib(n)并不是同时调用Fib(n-1)和Fib(n-2)，而是先调用其中一个，往深不断不断向下，建立n个栈帧，然后最深的那一层往回走的时候，右边和左边会调用同一个栈帧，所以自始至终只有n个栈帧在重复调用。从这里我们可以知道，空间是可以重复利用的。

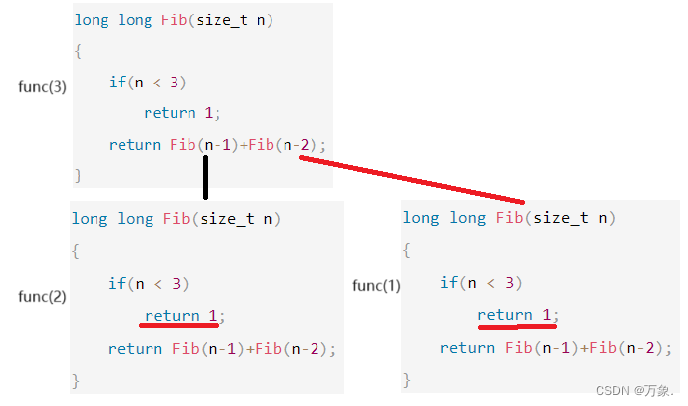
如上图，func(1)和func(2)公用同一个栈帧，可以用下图代码验证

void func1()
{
	int a=0;
	printf("%p\n",&a);
}
void func2()
{
	int a=0;
	printf("%p\n",&a);
}
int main()
{
	func1();
	func2();
	return 0;
}

运行结果如下图所示，两个地址是一样的（x64环境下）