看前提示:
篇幅较长,建议准备好草稿纸和笔还有水,边学边算,高数开始难起来了 (笔者也是预习得很疲惫RvR)
引语:
本章内容主要为多重(chóng)积分,在高数上中我们学过二阶三阶甚至高阶导数,现在我们即将学习二重以及三重积分,这俩在生活中应用比较多,再往上的四重五重积分就不是我们本科阶段要研究的内容,但是感兴趣的同学可以自己去搜索学习~
二重积分是二元函数在空间上的积分,同定积分类似,是某种特定形式的和的极限。本质是求曲顶柱体体积。
一、二重积分的基本计算
首先,二重积分形状长这样

∫∫ 符号:二重积分
f(x,y):被积二元函数
dɚ=dxdy
下面的D:积分区域,类似曲顶柱体的底面面积区域
积分结果:曲顶柱体的体积
方法:


1.直角坐标系计算二重积分

01图形:画出积分区域D的图形(注意:不是被积函数f(x,y)的)

02选坐标系:直角
03切片方向选择:看那个方向不是分段函数就选哪个,如果是切分x方向发现有分段函数,则改为切分y,如左下图,建议选择y型切法;例题这种,选哪个都行,我们先选择x型


x型:先积y再积x
y型:先积x再积y
选哪种切法就最后积哪个,切分方向影响积分顺序,积分顺序影响计算难度
04确定积分元素上下限:
现在选择x型,则先找y的上下限
沿y轴正方向看,y的下限为y=0这条线,上限为y=2-x
沿x轴正方向看,x的下限为0,上限为2
小方法:先积的元素上下限用后积的元素的函数表示,如果下限为0则写0;后积的函数上下限直接读图,写成纯数字
05列式计算
把积分拆开,按从右往左的顺序积分
注意积分元素,先积y则把式子里的x当作常数,求解关于y的定积分
下面是整个计算过程
练习一下,答案为333/20
2.极坐标系计算二重积分


极坐标系和直角坐标系的元素转换:(是的,要多做一步转换才能使用五步法)
ρ上下限:看圆的半径(0->半径)或者圆环大小径(小径->大径)
θ上下限:逆时针看角度上下限,起始位置为下限,结束位置为上限(角度读法,一圈为2π,45°为π/4)
积分顺序:先积ρ再积θ(固定的)
其他的按照五步法来计算即可
答案为:π(没算对再多算几遍√)
练习一下,答案为52π/3
二、二重积分的进阶计算
1.交换积分次序
1)直接考交换

交换积分次序,实际上是需要把x型和y型互换,原来为x型则改成y型,反之亦然
不需要算出结果,只要把变换后的式子写出来即可
方法:

以下为例题解题步骤:
01找函数:
根据上下限找到积分元素之间的关系
02画图:画出积分区域D的图形
03使用切片法重新切
04:列式写结果
2)被积函数不好算

观察(瞪眼法)发现:xe^xy先对y求定积分好算得多,然后想到交换积分次序
之后沿用上面的步骤计算一下结果吧0v0
答案为:
![]()
2.积分区域对称性解二重积分
1)关于坐标轴对称

观察(瞪眼法)发现:
1°被积函数很复杂
2°积分区域关于坐标轴对称
积分的奇偶对称性
记忆口诀:
轴对称,看奇偶(看D图是否存在轴对称)
x轴看y,y轴看x(D图关于x轴对称,则代入(x,y)和(x,-y)两个点进被积函数)
奇为0,偶成倍(若被积函数为奇函数,则积分结果为0)
2)关于y=x对称
积分的轮换对称性




x和y可以互换,即把所求转化成多元二重积分,再进行计算(就可以摆脱硬算带来的三角函数了)
这是硬算:(不太喜欢算这种定积分)
三、三重积分
这是三重积分的长相

∫∫∫ 符号:三重积分
f(x,y,z):被积函数(如果是密度函数,则积分结果为质量)
dxdydz:被积元素,有时候也写作 dv
下面的Ω:积分区域,立体图形
积分结果:立体图形的质量
方法:投影五步法
先求一次z的定积分,再求一次xy的二重积分

1.直角坐标系计算三重积分

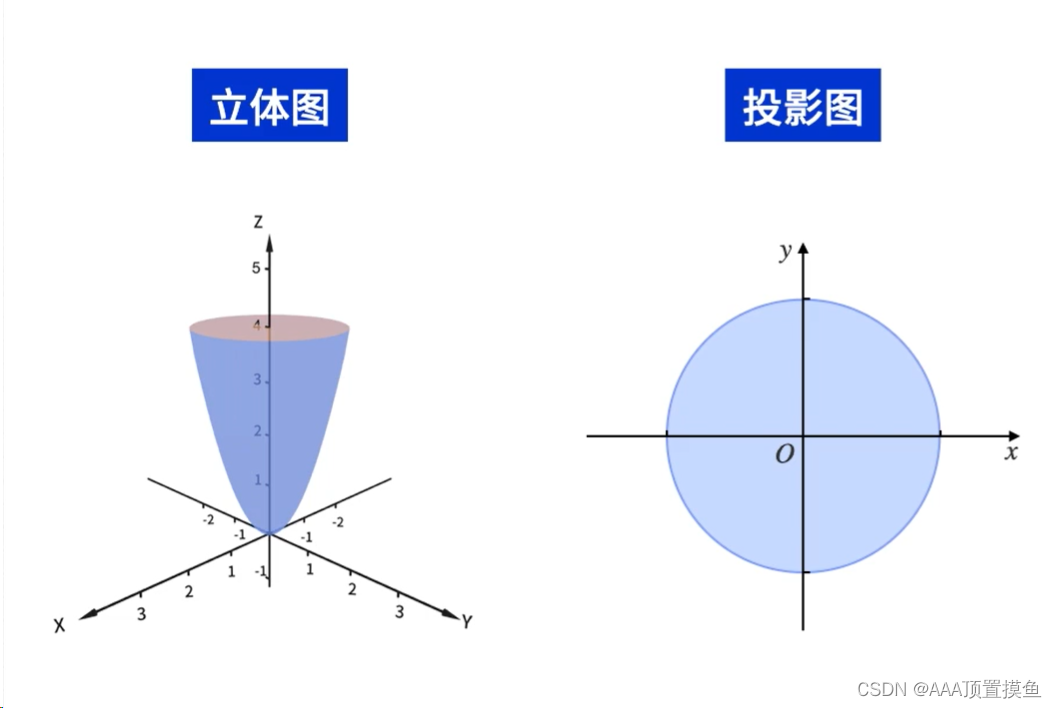
01画立体图和xoy面的投影图(俯视图):
02选坐标系:
03确定z的上下限:
把z表示成关于xy的函数
04确定xy的上下限:这里和前面的二重积分求法相同,笔者不过多赘述
05列式计算:三重转化为三次积分
答案为1/12
2.柱面坐标系计算三重积分
三重积分的柱面坐标系相当于二重积分的极坐标系

换元方法:

先积z再积ρ最后积θ
沿用上面的步骤自己计算一下结果吧0v0
列式计算,结果为32π/3
练习一下:
答案为π/2(^v^√)
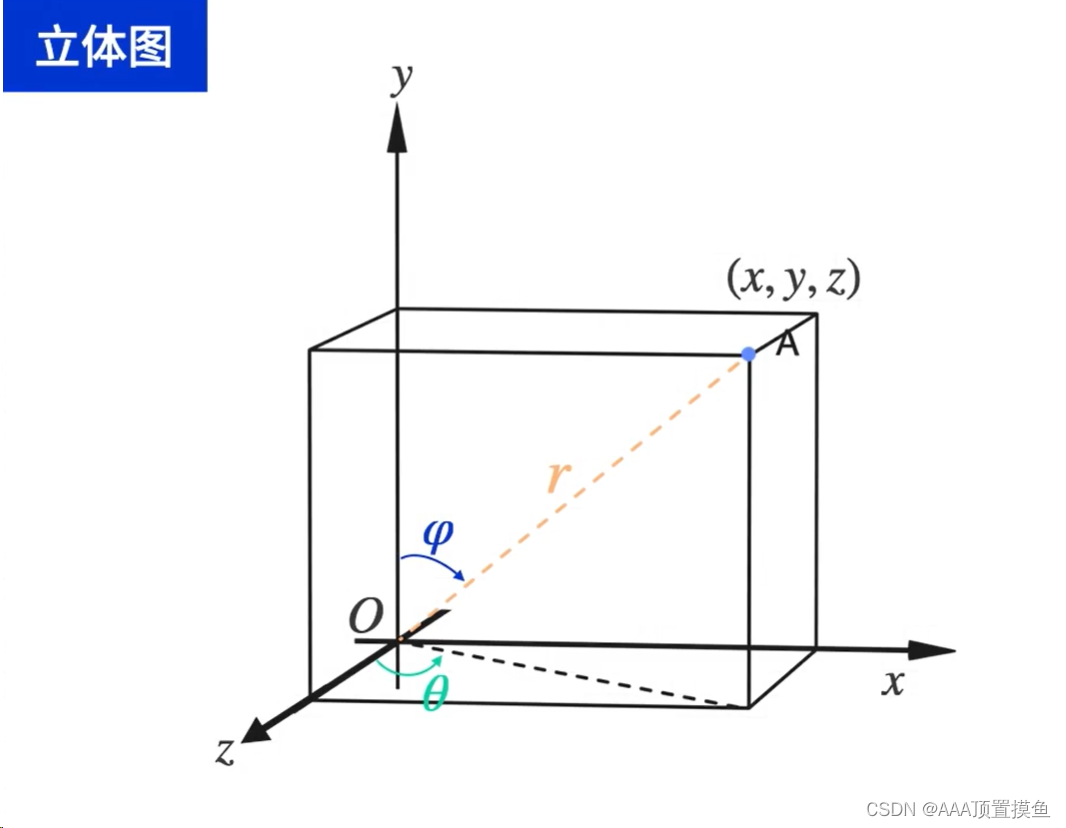
3.球面坐标系计算三重积分*(这个是拓展部分,不细讲,不考)
这是直角坐标系和球面坐标系的转换
以下为完整步骤:
4.三重积分的进阶算法

观察:不能硬算,需要找捷径(找合适的性质进行“消消乐”)

以下为解题过程:

总结:
考试遇到复杂的被积函数,先考虑是否有对称,能不能用性质简便计算,再看交换会不会好算一点,最后选择硬算,这个思考过程并不费时间,“三思而后行”,在练多几道题后,相信我们都会熟能生巧1v1

本章还涉及第一类曲面积分(对面积的曲面积分),也叫数量值函数的曲面积分,由于和下一章的两类曲面积分相合,笔者决定放在另一篇博文《章四-向量值函数的积分与场论》里面讲述,欢迎大家浏览
以上为笔者预习成果,如有不妥或指导之意,感谢各位评论和私聊~








 本文详细介绍了二重积分的基础概念、计算方法(直角坐标系和极坐标系),包括切片选择、积分顺序及区域确定。随后扩展到三重积分,探讨了直角坐标系和柱面坐标系的计算。文章强调了利用对称性、性质简化计算的重要性。
本文详细介绍了二重积分的基础概念、计算方法(直角坐标系和极坐标系),包括切片选择、积分顺序及区域确定。随后扩展到三重积分,探讨了直角坐标系和柱面坐标系的计算。文章强调了利用对称性、性质简化计算的重要性。




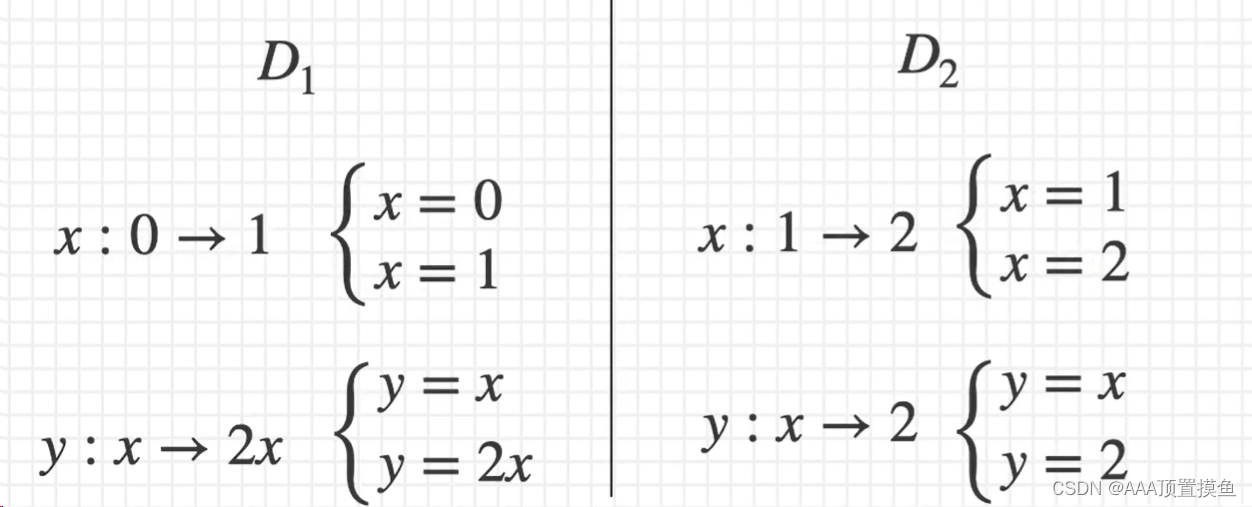











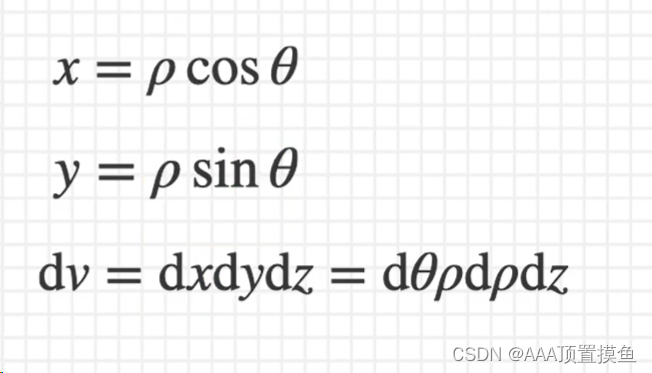




















 413
413

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








