区间合并问题（区间DP）

区间合并

区间合并问题通常指的是这样一类问题：给定一系列的区间，要求通过合并操作使得最终的区间数目最少或者通过某些规则使得最终的合并结果最优（例如最大化合并后的区间长度总和）。

区间合并问题的一般DP思路可以分为以下几个步骤：

1. 状态定义：
   对于区间合并问题，首先需要定义状态。通常状态会涉及到区间的起点和终点，即dp[i][j]表示从区间i到区间j的合并结果的最优值。

2. 状态转移方程：
   接下来需要定义状态转移方程，这是动态规划中最核心的部分。对于区间合并问题，状态转移方程通常会考虑如何从小的区间合并到大的区间。例如，我们可能会考虑将区间[i, k]和[k+1, j]合并成[i, j]，那么状态转移方程可能会是这样的形式：
   dp[i][j] = min/max(dp[i][j], dp[i][k] + dp[k+1][j] + cost(i, k, j))
   其中cost(i, k, j)是将两个区间合并起来的代价，具体取决于问题的要求。在合并石子这道问题中，最后两个区间的合并代价直接用前缀和求即可。
   

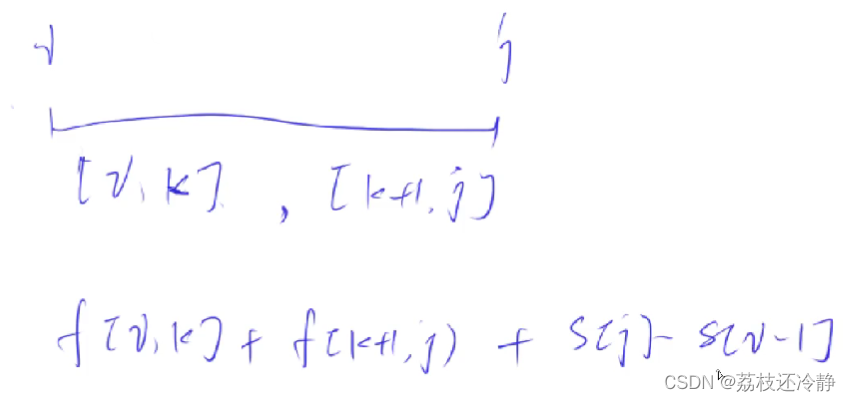
3. 初始化条件：
   动态规划需要有初始状态，对于区间合并问题，通常初始化条件是单个区间的情况，即dp[i][i]，这通常是一个已知的值或者是一个基本情况。

4. 计算顺序：
   由于区间合并问题的子问题依赖于更小的区间，因此计算顺序通常是按照区间长度从小到大进行的。先计算所有长度为1的区间的dp值，然后是长度为2的区间，以此类推。

5. 结果提取：
   最后，根据问题的要求提取结果。如果问题要求合并所有区间的最优结果，则查看dp[1][n]的值（假设区间是从1到n）。如果问题有其他要求，可能需要从不同的状态中提取结果。

在实际应用中，根据具体问题的不同，上述步骤可能需要进行相应的调整。例如，有些问题可能需要记录合并路径，有些问题可能有特殊的合并规则等。总之，设计DP时需要根据问题的具体要求来定义状态、转移方程和初始化条件，并且选择合适的计算顺序来确保所有状态都能被正确计算。

自底向上（Bottom-Up）的动态规划解法:

//区间dp问题还是有一定模板可循的
//你想获得一个大区间的值，势必要提前处理完更小区间的值
//如果是传统的先枚举左端点，再枚举右端点，再枚举分割区间点，会违背上面的原则，在你枚举右端点的时候区间长度是在递增的
//而f[1][4] 当k=1时，我只知道f[1][1]的值，却不知道f[2][4]的值，因为只有当i枚举到2，j枚举到4时才会开始计算这个值
//所以，我们需要先枚举长度，在确保计算区间长度为5时，已经把所有区间长度更小的情况全部计算过
//这时我们需要枚举左端点，由于长度以及确定，所以右端点为i+len-1。这样我们可以确保在分割时所有更小的情况都被处理过
#include<iostream>
using namespace std;
const int N=310,INF=0x3f3f3f3f;
int s[N];
int f[N][N];
int main()
{
    int n;
    cin>>n;
    //前缀和数组
    for(int i=1;i<=n;i++){
        cin>>s[i];
        s[i]+=s[i-1];
    }
    
    //len==1时，f[l][r]=0;因为只有一堆，不需要合并，消耗为0
    //len>=2时，f[l][r]=INF;此时可拆分，如果f[l][r]全部初始化为0，f[l][r]<f[l][k]+f[k+1][r]+s[r]-s[l-1],即永远是0
    
    for(int len=2;len<=n;len++){//枚举区间长度
        for(int i=1;i+len-1<=n;i++){//枚举区间左端点
            int l=i,r=i+len-1;//获取长度为len的区间的左右端点
            f[l][r]=INF;
            for(int k=l;k<r;k++){//枚举分割点
                f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
            }
        }
    }
    cout<<f[1][n];//三重循环o(n^3)
    return 0;
}

---

对于这类问题，我们也可以使用记忆化搜索（也称为自顶向下，Top-Down）的动态规划解法。在转换为记忆化搜索的过程中，我们需要将原来的循环结构改为递归结构，并且添加一个记忆数组用于存储已经计算过的子问题的结果。

#include<iostream>
using namespace std;
const int N = 310;
int f[N][N];
int s[N];
int n;

// 定义记忆化搜索函数
int dp(int l, int r) {
    // 如果已经计算过，则直接返回结果
    if (f[l][r] != -1) return f[l][r];
    // 单个区间的情况
    if (l == r) return 0;
    // 初始化结果为无穷大
    f[l][r] = 0x3f3f3f3f;
    // 遍历所有可能的分割点
    for (int k = l; k < r; k++) {
        f[l][r] = min(f[l][r], dp(l, k) + dp(k+1, r) + s[r] - s[l-1]);
    }
    return f[l][r];
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> s[i];
        s[i] += s[i-1];
    }
    // 初始化记忆数组
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            f[i][j] = -1;
    cout << dp(1, n);
    return 0;
}

这里的dp函数，和一般的dfs函数并无不同，但加上了所谓的记忆化，其实就是把每次递归这个分支上计算出的结果存储下来，万一下次需要用到的某个数据dfs下去会走到这个分支，就可以直接返回得出答案了~

对于dfs问题我一向是不打算深思的，不然容易钻牛角尖，你只需要知道这个dfs函数的含义、参数、出口、然后用就是了！比如这里，参数:一个区间，含义:返回这个区间内所有合并方式中的最小代价。此时你在来看下面这个式子不就水到渠成了。

for (int k = l; k < r; k++) {//枚举分界点
        f[l][r] = min(f[l][r], dp(l, k) + dp(k+1, r) + s[r] - s[l-1]);
        //记录所有被划分的两个子区间的最小合并代价+最后一次合并总代价，即l~r区间的最小合并代价
    }