动态规划之礼物的最大数量问题

一.题目描述

这就是本题的题目，题目很简单，如图所示

1	3	1
1	5	1
4	2	1

每一个格中的数字表示在此处我们可以获取的礼物，从左上角的位置出发，到达右下角的位置，要求每次只能向右或向下移动一格

二.讲解算法原理

1.状态表示

我们定义一个二维数组dp，dp[i][j]表示到达第i+1行，第j+1列时，获得的礼物总数（包括此处的礼物）

 

2.状态转移方程

 

		1
	2

 

所以dp[i][j]=max(dp[i-1][j]+g[i][j],dp[i][j-1]+g[i][j-1];

3.初始化

当[i][j]表示如下位置时，会出现越界行为

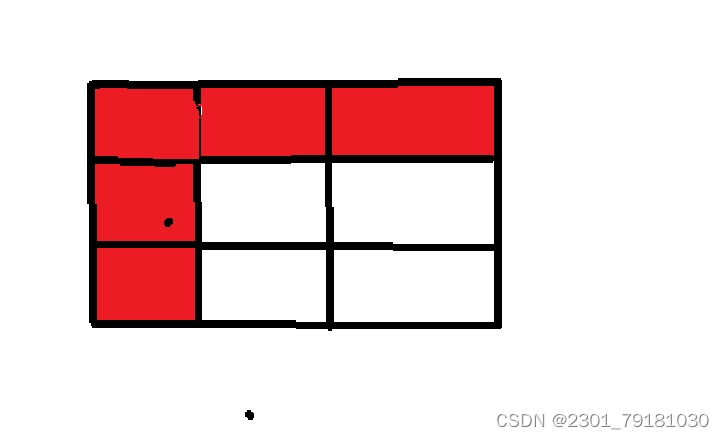
所以我们要这样

所以，我们需要开辟一个4行，4列的二维数组，

在这里有两个注意的地方

1.新加的绿色的地方填的值要保证后面的填表是正确的

2.下标的映射

因为是用的是最大值，所以我们在新加的几个位置里设0即可，由于我们使用的是vector，默认会存放0，所以我们不需要进行相关的操作。

4.填充顺序

因为我们是从左上角到右下角，所以，我们进行填充的顺序是从上往下，同行，从左往右依次进行填充，

5.返回值

关于返回值问题，由于本来是m*n的数组，我们加了一行一列，所以右下角的位置就变成了[m][n],

返回的便是dp[m][n]。

三.代码实现

class Solution
{
 public:
    int maxValue(vector<vector<int>>& grid)
    {
        //1.创建dp表
        //2.初始化
        //3.填表
        //3.返回结果
       int m=grid.size();
       int n=frid[1].size();
       vector<vector<int>> dp(m+1,vector<int>(n+1));
       for(int i=1;i<=m;i++)
       {
           for(int j=1;j<=n;j++)
           {
                dp[i][j]=max(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];
           }
       }
        
       return dp[m][n];

            
    }
}